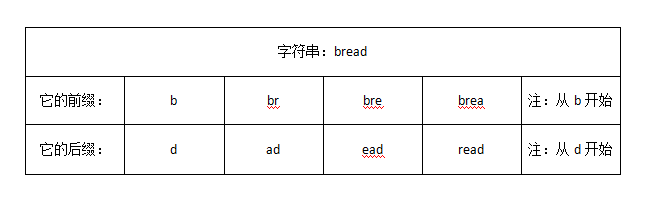
前言需求
前面讲解了动态规划的思想,今天我们要说的是涉及字符串匹配问题(KMP)
现在前来看我们的问题
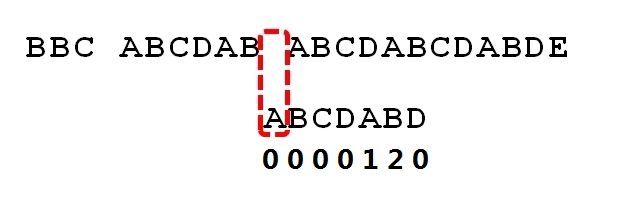
1.字符串 str1 = "BBC ABCDAB ABCDABCDABDE"
2.字符串 str2 = "ABCDABD"
现在要判断 str1 是否含有 str2, 如果存在,就返回第一次出现的位置, 如果没有,则返回-1
那么你觉得你会是怎么做的呢?
一、小明同学的思路想法
小明同学:我先找到符合str2 字符串的第一个'A'的位置
小明同学:将str2 的字符串一个一个的进行匹配否相等
那么小明同学的这种思路呢,我们称为:暴力匹配
我们假设现在str1匹配到 i 位置,子串str2匹配到 j 位置,则会:
1.匹配成功(即str1[i] == str2[j]),则i++,j++,继续匹配下一个
2.匹配失配(即str1[i]! = str2[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯,j 被置为0
public static int violenceMatch(String str1,String str2){
char[] s1 = str1.toCharArray();
char[] s2 = str2.toCharArray();
int s1Len = s1.length;
int s2Len = s2.length;
int i = 0;//i索引指向s1
int j = 0;//j索引指向s2
while(i我们可以使用demo 测试一下这种方法
public static void main(String[] args) {
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "ABCDABD";
int index = violenceMatch(str1,str2);
System.out.println(index);
}
运行结果如下:
15二、小王同学的思路想法
小王同学:小明同学的方法虽然是可以完成找到,但是也有不好的地方
1.当匹配失败时候,就回溯重新进行匹配,这样的方法很复杂同时效率很慢
2.当匹配成功时候,才直接把i 的位置 - j的位置
小王同学:我知道一个算法,它比较适合做这样的事情:KMP 算法
三、什么是KMP 算法
Knuth-Morris-Pratt 字符串查找算法,简称为 “KMP算法”,常用于在一个文本串S内查找一个模式串P 的出现位置
KMP方法算法就利用
1.之前判断过信息,通过一个next数组,保存模式串中前后最长公共子序列的长度。
2.每次回溯时,通过next数组找到,前面匹配过的位置,省去了大量的计算时间
ok,什么意思?不懂没关系,我们一步一步来分析。
图解分析暴力匹配引入KMP
按照小明同学的思路,字符串Str1 与 字符串 Str2匹配 ,不满足则下一个匹配
一直重复匹配,直到Str1 与Str2 有一个字符匹配符合为止
接着比较下一个字符串,还是匹配符合
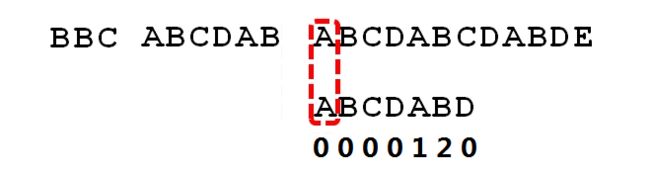
直到遇到Str1有一个字符串与Str2 对应的字符串(D与空格)不符合
这个时候就回溯,又进行重新的匹配,从 B 与 A 匹配
其实这是很不明智的,因为此时BCD已比较过了,没有必要做重复的工作,当空格与D不匹配的时候,其实你已知道前面六个字符是“ABCDAB”
KMP 算法的想法是:设法利用这个已知信息,不要把”搜索位置”移回已经比较过的位置,继续把它向后移,这样就提高了效率
步骤图解分析KMP的想法
这里怎么理解呢,一起画图来解释看看,当我们回溯重新匹配的时候
发现 B 与A不符合 那么进行下一个,C与A匹配
发现 C 与A不符合 那么进行下一个,D与A匹配....以此类推
当A与A匹配的时候,那么又执行了B与B比,空格与C比,这样的重复
我们发现没有,BCD就已比较过了,所以我们不要把”搜索位置”移回已经比较过的位置
步骤图解分析的问题发现
如果我们知道这个A和后面的BCD是不相同的,那么这样的比较就没有意义的
那么有个问题需要思考一下:我们怎么知道这些比较会不相同呢?
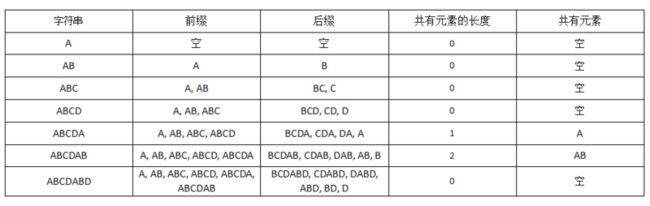
这里就涉及到一个部分搜索词:字符串前缀与后缀公共的部分
我们可以创建一个搜索词(部分匹配表)
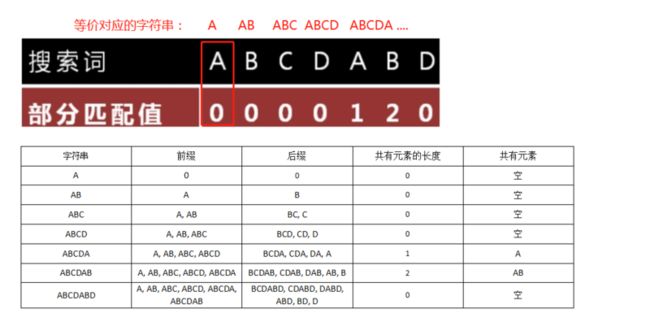
在此之前,我们知道0000120是什么?怎么来的?为什么是这样的
这就要先说说字符串的前缀与后缀了
KMP的搜索词(部分匹配表)分析
现在你知道0000120 是怎么来的吗?每个匹配值你应该知道对应的是什么
ok,回到刚刚我们提出的那个问题:我们怎么知道这些比较会不相同呢?
现在根据部门匹配值 你是有点思路的想法嘛?
四、通过一坨代码来验证思想KMP
首先我们先将字符串的部分匹配表弄出来,一起来看看代码是怎么做的?
public static int[] kmpNext(String dest){
//创建一个next数组保存部门匹配值
int[] next = new int[dest.length()];
//dest的字符个数只有一个,则直接 = 0;
next[0] = 0;
for(int i = 1,j = 0;i < dest.length() ; i++){
//kmp 算法的思想 相当于是回溯,一直往前比较
while(j>0 && dest.charAt(i) != dest.charAt(j)){
j = next[j-1];
}
if(dest.charAt(i) == dest.charAt(j)){
j++;
}
next[i] = j;
}
return next;
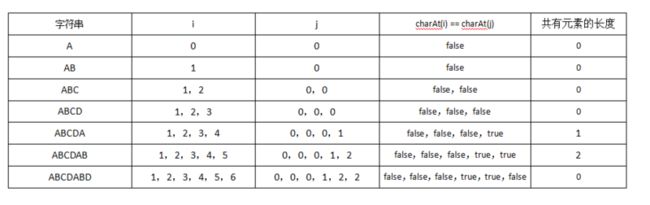
}好,这代码是什么情况?为什么dest.charAt(i) == dest.charAt(j)?
我们刚刚表格是从字符串的头开始分析的,还记得吗? 代入进去我们验证一下
这个时候,有的小伙伴就有点懵逼了,为什么要执行while循环多一层判断呢?
这里的目的是要回溯,不然的话j++ 会造成以下的效果
通过例子来体会KMP思想
我们使用一个例子来demo与查找方法体会一下
public static int kmpSearch(String str1,String str2){
for(int i = 0,j = 0;ipublic static void main(String[] args) {
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "BBC";
System.out.println("index = "+ kmpSearch(str1,str2));
}
运行结果如下:
index = 01.当我们进行匹配BBC的时候,charAt(i) == charAt(j) 是满足的,j++
2.当j =3 时,也等于BBC字符串的长度,这时我们代表找到了,这时i = 2
3.因为charAt(2) = C,只需要使用i - j + 1 则代表开始index坐标
问题发现
public static void main(String[] args) {
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "ABCDABD";
System.out.println("index = "+ kmpSearch(str1,str2));
}
运行结果如下:
index = 8当我们将BBC换成ABCDABD的时候,结果就出现问题了index = 8
为什么会这样呢?
那是因为我们没有考虑不相等的情况,只考虑的相等的情况++
1.当我们不断的判断满足的时候,str2字符串只剩下D没匹配
2.str1 对应的i 字符:空格、A、B、C都不满足,一直到D 这时j++
3.这时的条件满足了,但是不是我们想要的结果,所以我们需要考虑不相等
public static int kmpSearch(String str1,String str2,int next[]){
for(int i = 0,j = 0;i0 && str1.charAt(i) != str2.charAt(j)){
j = next[j-1];
}
if(str1.charAt(i) == str2.charAt(j)){
j++;
}
if(j == str2.length()){
return i - j +1;
}
}
return -1;
} public static void main(String[] args) {
String str1 = "BBC ABCDAB ABCDABCDABDE";
String str2 = "ABCDABD";
int [] next = kmpNext(str2);
System.out.println("index = "+ kmpSearch(str1,str2,next));
}五、步骤图演示KMP算法
那么接下来我们使用KMP算法图解的方式走一遍
首先先求出Str2 的部分匹配值
这时,我们从这里开始讲解,一步一步的来,A与A匹配,此时j++
直到遇到Str1有一个字符串与Str2 对应的字符串(D与空格)不符合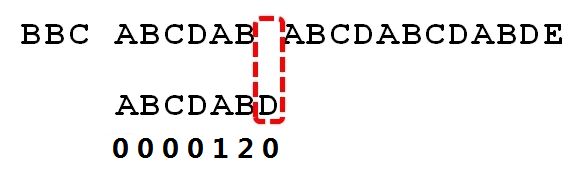
此时(D与空格)不符合,那么J回溯到对应的匹配值,继续匹配
此时(C与空格)不符合,那么J回溯到对应的匹配值,继续匹配
此时(A与空格)不符合,所以接着Str1 字符串 i++ 进行下一个匹配,匹配上就j++ 以此类推
因为此时BCD已比较过了,没有必要做重复的工作,当空格与D不匹配的时候,其实已知道前面六个字符是“ABCDAB”
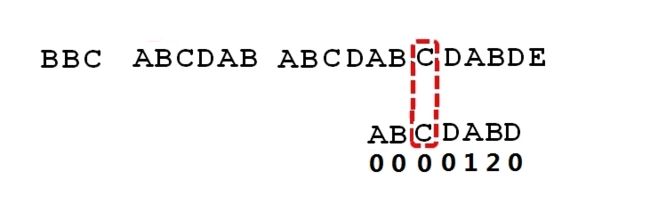
直到遇到Str1有一个字符串与Str2 对应的字符串(D与C)不符合
此时(D与C)不符合,那么J回溯到对应的匹配值,继续匹配
下一个匹配,B与B匹配,此时j++..以此类推..
此时我们的回溯是在部分匹配表里进行的,而不是从Str1 进行回溯,根据图解你能看出小明同学的思路与小王同学的思路区别么?