【算法百题之三十九】年轻人不讲武德，5分钟学会A*算法

  【算法百题之三十九】年轻人不讲武德，5分钟学会A*算法

 

     大家好，我是Lampard~~

     很高兴又能和大家见面了，接下来准备系列更新的是算法题，一日一练，早日升仙！

     今天的探讨的问题是：实战8方向A*寻路算法。

      【A*入门博客1】

      【A*入门博客2】

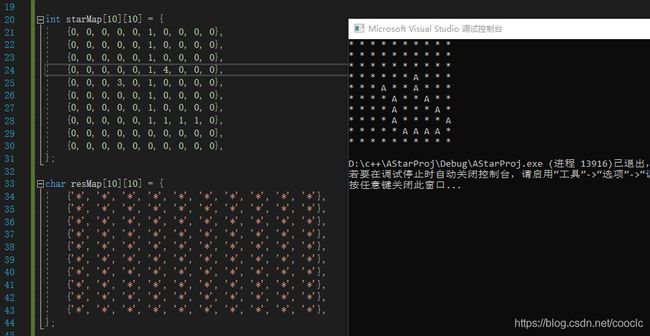
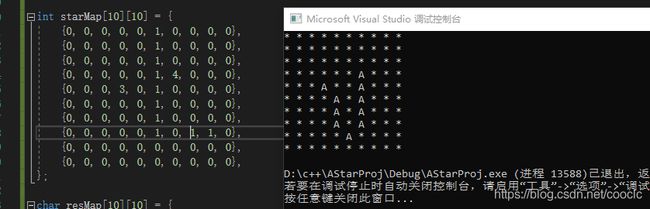
    若对A*概念不熟悉的年轻人们可以先看看上面两篇博客，我觉得概念解释得很不错的。今天主要和大家一起代码实战A*，先上效果图：

   

（1）A*算法的主要构成

  在我看来，A*寻路的构成主要由三部分组成：

• 启动列表
• 关闭列表
• 地图块结点

（1）启动列表

  存放有可能将要经过的地图块。

（2）关闭列表

  存放不会遍历的地图块，注意不会遍历不代表没有经过，有可能是从启动列表移除出来的。

（3）地图块结点

  我们把一张大地图划分成一个个规整的地图块，我们需要定义一个结点来代表这个地图块。而地图块结点中有几个比较重要的属性：

1.自己所处的行列的位置，2.H值，H值是欧几里得距离，即从当前位置到目的点的直线距离，3。G值，从起点到当前位置产生的耗费，4.F值（路径的长度） = G + H

（2）A*算法寻路过程

1. 先把起点放到启动列表中
2. 在启动列表中找到路径(f)最短的格子
3. 将之父节点设置为起点
4. 将其周围的格子放入启动列表中（已经在开启或者关闭列表中的结点则不需要放入）
5. 把该结点从启动列表移动到关闭列表
6. 当在启动列表中找到终点的时候结束

（3）原理就这么简单，上代码！！！

 为了方便测试，我们用一个10*10的二维数组来代表我们的地图，其中3是起点，4是终点，1是障碍物，0是可走路径

int starMap[10][10] = {
	{0, 0, 0, 0, 0, 1, 0, 0, 0, 0},
	{0, 0, 0, 0, 0, 1, 0, 0, 0, 0},
	{0, 0, 0, 0, 0, 1, 0, 0, 0, 0},
	{0, 0, 0, 0, 0, 1, 4, 0, 0, 0},
	{0, 0, 0, 3, 0, 1, 0, 0, 0, 0},
	{0, 0, 0, 0, 0, 1, 0, 0, 0, 0},
	{0, 0, 0, 0, 0, 1, 0, 0, 0, 0},
	{0, 0, 0, 0, 0, 1, 1, 1, 1, 0},
	{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
	{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
};

  然后我们定义一下地图块结点，把刚才我们说到的几个属性定义上去。记得不要忘记parent字段，这是回溯找起点找路径的指针，很重要

struct stNode {
	int row;
	int col;
	int f;            // 路径的长度：f = g + h
	int g;			  // 从起点到当前路径产生的耗费
	int h;		      // 预估值欧几里得距离，即从该点到目的点的直线距离
	stNode* parent;   // 父节点，用于索引找起点
};

然后我们就开始写我们的main函数啦~首先循坏一波，要从我们声明的地图中找到我们的起始和开始的位置。

int main() {
	// 确认开启与结束结点
	int rowStart, colStart, rowEnd, colEnd;
	for (int i = 0; i < 10; i++) {
		for (int j = 0; j < 10; j++) {
			if (starMap[i][j] == 3) {
				rowStart = i;
				colStart = j;
			}

			if (starMap[i][j] == 4) {
				rowEnd = i;
				colEnd = j;
			}
		}
	}
    
	return 0;
}

 然后是根据得到的位置构建我们的其实和终止结点，对于终止位置来说只需要给它赋值行列坐标就可以了。对于其实坐标我们还需要对其其他几个属性赋值。首先是g值，因为本身自己就是起点，所以起点到自己的距离就是0；然后是h值，这里我们可以用一个函数distance来计算两点之间的距离。其中ITEM_W是各自的宽高，然后简单勾股定理就可以了。之后再把f值赋值成h+g即可，起点的parent是空，也就是说找到自己为止。

int distance(int rowStart, int colStart, int rowEnd, int colEnd) {
	int x1 = rowStart * ITEM_W + ITEM_W / 2;
	int y1 = colStart * ITEM_W + ITEM_W / 2;
	int x2 = rowEnd * ITEM_W + ITEM_W / 2;
	int y2 = colEnd * ITEM_W + ITEM_W / 2;

	return (int)sqrt((float)(pow((x1 - x2), 2) + pow((y1 - y2), 2)));
};

    // 构建开始结点和结束结点
	stNode* nodeStart = new stNode;
	nodeStart->row = rowStart;
	nodeStart->col = colStart;
	nodeStart->g = 0;
	nodeStart->h = distance(rowStart, colStart, rowEnd, colEnd);
	nodeStart->f = distance(rowStart, colStart, rowEnd, colEnd);
	nodeStart->parent = NULL;

	stNode* nodeEnd = new stNode;
	nodeEnd->row = rowEnd;
	nodeEnd->col = colEnd;

然后就是构建我们的启动和关闭列表。这里我们使用链表作为存储工具（实际使用二叉树会更有效率），然后再按照我们的算法第一步，把起点给放入开启列表中。

	// 构建开启和关闭列表
	list openList;
	list closeList;
	openList.push_back(nodeStart);
	stNode* curNode = NULL;

紧接着就是开始我们算法的过程进入循环。首先我们要确认算法的终点：这个算法有两种时候会跳出循环，其一是按照流程最后在开启列表中找到终点的时候。其二是从启动列表中找最短路径的结点的时候，若找不到则证明开启列表没有结点，也就证明根本就没有路可以过去，因此这个时候也要跳出循环。我们用getNearNode来寻找启动列表中最短路径的结点。然后用getNearListNode函数来找到当前结点前后左右，左上左下右上右下8个结点（注意算法的第4点，已经在启动和关闭列表的不要放，不然会造成死循环），找到之后把当前节点放入关闭列表中，然后用removeNode函数把它从启动列表中移除。最后再把刚才找到的附近的结点，塞进启动列表中即可。短短十数行代码则已经完成了整个A*思路。

while (!isNodeInList(openList, nodeEnd)) {
		curNode = getNearNode(openList);
		if (curNode == NULL) {
			cout << "找不到可选路径" << endl;
			break;
		}

		list nearListNode;
		getNearListNode(curNode, nearListNode, openList, closeList, nodeEnd);
		closeList.push_back(curNode);
		removeNode(curNode, openList);

		for (list::iterator it = nearListNode.begin(); it != nearListNode.end(); it++) {
			openList.push_back(*it);
		}
	}

现在我们来看看刚才提及的几个函数，首先是getNearNode函数。emm这个很简单嘛，就是遍历链表找出最F值最小的结点。用个指针存当前最小结点就可以了

// 拿到f路径最小的结点
stNode* getNearNode(list &openList) {
	stNode* minNode = NULL;
	int tmpF = 100000;
	for (list::iterator it = openList.begin(); it != openList.end(); it++) {
		if ((*it)->f < tmpF) {
			minNode = *it;
			tmpF = minNode->f;
		}
	}
	return minNode;
}

然后再看看removeNode这个方法，这个更简单，就是遍历一遍结点然后把当前结点移除即可。若迭代器的行列数和当前结点的相同，则使用erase函数移除。

// 从列表中移除当前结点
void removeNode(stNode* curNode, list &openList) {
	for (list::iterator it = openList.begin(); it != openList.end(); it++) {
		if ((*it)->row == curNode->row && (*it)->col == curNode->col) {
			openList.erase(it);
			break;
		}
	}
}

有点难度的是getNearListNode这个方法，其一要将当前结点3*3（不包含自己）的8个结点给记录下来，而且还不能在启动和关闭链表中。我们首先可以x轴加减一找出左边和右边的结点，然后y轴加减一找出上边和下边的结点。因此我们我可以使用一个双重循环i从-1到1，j从-1到1来实现这一点。当然当i,j都=0时则代表当前结点本身，则直接跳过即可。当我们找到这8各节点之后还要对此进行筛选，首先我们要排除越界的情况，就是横轴坐标已经超出地图那肯定是不行滴。然后是判断是不是阻断点，若地图该结点位置的值为1则代表是阻断点，那么我们同样跳过。最后是判断该节点是否在启动或者关闭列表中，若是的话则跳过。所有的条件都满足的话我们就把这个结点记录下来，等待塞入启动列表中。

// 把curNod旁边3*3的8个结点且不在开启或关闭列表都放进nearNodelist中
void getNearListNode(stNode* curNode, list &nearNodeList, list &openList, list & closeList, stNode* endNode) {
	for (int i = -1; i <= 1; i++) {
		for (int j = -1; j <= 1; j++) {
			if (i == 0 && j == 0) continue;
			int rowTmp = curNode->row + i;
			int colTmp = curNode->col + j;
			
			// 判断是否越界
			if (rowTmp < 0 || rowTmp > 9 || colTmp < 0 || colTmp > 9) continue;

			// 判断是不是阻挡点
			if (starMap[rowTmp][colTmp] == 1) continue;

			// 在开启或者关闭列表中
			stNode* nearNode = new stNode;
			nearNode->row = rowTmp;
			nearNode->col = colTmp;
			if (isNodeInList(openList, nearNode) || isNodeInList(closeList, nearNode)) {
				continue;
			}

			nearNode->g = curNode->g + distance(curNode->row, curNode->col, nearNode->row, nearNode->col);
			nearNode->h = distance(endNode->row, endNode->col, nearNode->row, nearNode->col);
			nearNode->f = nearNode->g + nearNode->h;
			nearNode->parent = curNode;
			nearNodeList.push_back(nearNode);
		}
	}
}

就这样整个A*的过程已经完成，之后就是为了方便校验结果，我们可以这样输出结果：若是没有最短的路径则返回没有可选路径，若正常找到路径，则可以通过其parent的指针回溯找到起点，然后把这条路的结点都换成A输出结果

	if (curNode == NULL) {
		cout << "找不到可选路径" << endl;
		return 0;
	}

	stNode* findNode = NULL;
	for (list::iterator it = openList.begin(); it != openList.end(); it++) {
		if ((*it)->row == rowEnd && (*it)->col == colEnd) {
			findNode = *it;
			break;
		}
	}

	stNode* node = findNode;
	while (node != NULL) {
		resMap[node->row][node->col] = 'A';
		node = node->parent;
	}

	for (int i = 0; i < 10; i++) {
		for (int j = 0; j < 10; j++) {
			cout << resMap[i][j] << " ";
		}
		cout << endl;
	}

 

【各寻路算法代码下载链接】

A*的分享就到这里啦，年轻人要耗子尾汁！