Matlab通过市场数据校准Hull-White利率模型参数
原文链接:http://tecdat.cn/?p=17973
利率衍生证券的定价依赖于描述基本过程的模型。这些利率模型取决于您必须通过将模型预测与市场上可用的现有数据进行匹配来确定的一个或多个参数。在Hull-White模型中,有两个与短期利率过程相关的参数:均值回归和波动率。
对于Hull-White模型,关于均值回归(α)和波动率(σ)最小化是二维的。也就是说,校准Hull-White模型可最大程度地减少模型的预测价格与观察到的市场价格之间的差异。
Hull-White校准案例
使用市场数据来识别为构建工具定价的Hull-White树所需的隐含波动率(σ)和均值回归(α)系数,必须对市场数据进行插值。
考虑具有以下参数的上限:
Strike = 0.0690;
Reset = 4;
Principal = 1000;
datestr(capletDates')ans =
21-Mar-2008
21-Jun-2008
21-Sep-2008
21-Dec-2008
21-Mar-2009
21-Jun-2009
21-Sep-2009
21-Dec-2009
21-Mar-2010
21-Jun-2010
21-Sep-2010
21-Dec-2010
21-Mar-2011在最佳情况下,查找带有Strike =的 市场波动率 0.0690,以及列出的到期日,但找到这些确切数据的可能性很小。结果,使用市场上可用的数据并进行插值。
根据市场数据,您可以获得不同日期和行使价的上限信息。
| 到期 | 协议1 = 0.0590 | 协议2 = 0.0790 |
|---|---|---|
| 2008年3月21日 | 0.1533 | 0. 1526 |
| 2008年6月21日 | 0.1731 | 0. 1730 |
| 2008年9月21日 | 0. 1727 | 0. 1726 |
| 2008年12月21日 | 0. 1752 | 0. 1747 |
| 2009年3月21日 | 0. 1809 | 0. 1808 |
| 2009年6月21日 | 0. 1809 | 0. 1792 |
| 2009年9月21日 | 0. 1805 | 0. 1797 |
| 2009年12月21日 | 0.1802 | 0. 1794 |
| 2010年3月21日 | 0.1802 | 0. 1733 |
| 2010年6月21日 | 0. 1757 | 0. 1751 |
| 2010年9月21日 | 0. 1755 | 0. 1750 |
| 2010年12月21日 | 0. 1755 | 0. 1745 |
| 2011年3月21日 | 0. 1726 | 0. 1719 |
要求日期,协议价和实际波动分为三个变量: MarketStrike, MarketMat,和 MarketVol。
MarketStrike = [0.0590; 0.0790];
MarketMat = {'21-Mar-2008';
'21-Jun-2008';
'21-Sep-2008';
MarketVol = [0.1533 0.1731 0.1727 0.1752 0.1809 0.1800 0.1805 0.1802 0.1735 0.1757 ...
使用此数据完成输入参数 RateSpec:
RateSpec =
FinObj: 'RateSpec'
Compounding: 4
Disc: [14x1 double]
Rates: [14x1 double]
EndTimes: [14x1 double]
StartTimes: [14x1 double]
EndDates: [14x1 double]
StartDates: 733428
ValuationDate: 733428
Basis: 0
EndMonthRule: 1调用校准例程以找到波动率参数Alpha和Sigma的值
根据市场数据计算的值 Alpha ,Sigma 。例如,您可以将目标函数的公差定义为 100*eps :
Local minimum possible.
> In hwcalbycapfloor at 93
In hwcalbycap at 75
Alpha =
1.0000e-06
Sigma =
0.0127先前的警告表明转换不是最佳的。使用的搜索算法未找到符合所有约束的解决方案。要辨别该解决方案是否可接受,请通过为以下项指定第三个输出(OptimOut)来查看 优化结果:
hwcalb(RateSpec, MarketStrike, MarketMat,...
结构的 OptimOut.residual 字段 OptimOut是优化残差。此值包含Black caplet和优化过程中计算出的值之间的差异。您可以使用该 OptimOut.residual 值计算与Black Caplet价格相比的百分比差异(误差),然后确定残差是否可以接受,决定是否接受以单一数值参数化的市场 Alpha 和 Sigma。
使用市场数据和Black模型获取价格
Black -76模型被认为是世界范围内广泛接受的互换期权定价模型,互换期权计算公式看起来和期权价格公式一 样,这表示在使用Black模型对互换期权进行定价时,可以用和定价期权时同样的方法进行计算.为了使Black模型生效,只需输入由市场决定的隐含波动率即可。
为了确定优化的有效性,请使用Black公式和市场数据计算参考值。请注意,您必须首先对市场数据进行插值以获得用于计算的数据量:
FlatVol = interp2(Mats, Strikes, MarketVol, datenum(Maturity), 使用Black模型计算价格:
capbybike, Settle, Maturity, FlatVol,...
Caplets =
0.3210
1.6355
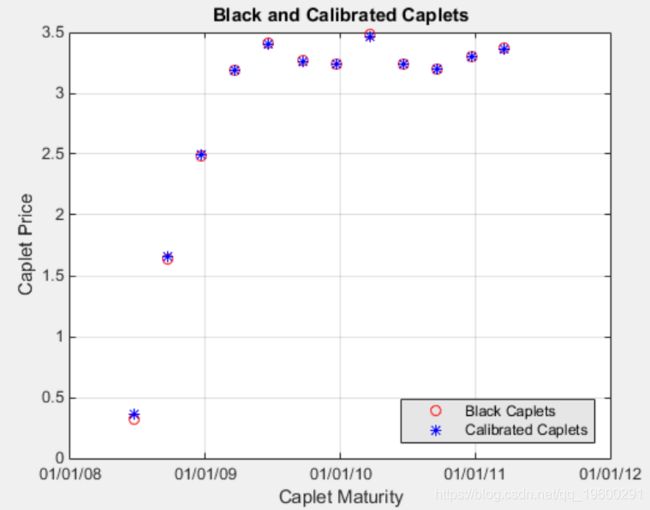
比较优化值和Black值并以图形方式显示
在计算了参考值之后,请通过分析和图形方式比较这些值,以确定是否计算出的单个值 Alpha 并 Sigma 提供适当的近似值:
plot(MarketMatNum(2:end), Caplets, 'or', MarketMatNum(2:end), O
ylabel('Caplet Price');
t
set(gcf, 'NumberT使用Black,HW分析和HW树模型比较上限价格
最受欢迎的见解
1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用
2.R语言GARCH-DCC模型和DCC(MVT)建模估计
3.R语言实现 Copula 算法建模依赖性案例分析报告
4.R语言COPULAS和金融时间序列数据VaR分析
5.R语言多元COPULA GARCH 模型时间序列预测
6.用R语言实现神经网络预测股票实例
7.r语言预测波动率的实现:ARCH模型与HAR-RV模型
8.R语言如何做马尔科夫转换模型markov switching model
9.matlab使用Copula仿真优化市场风险
使用Black模型,Hull-White分析模型和Hull-White树模型比较相应上限价格。