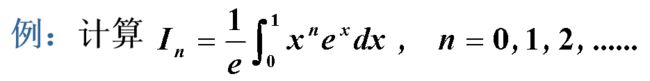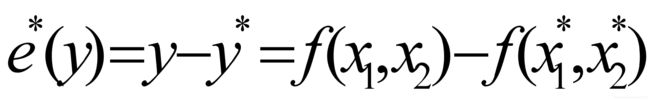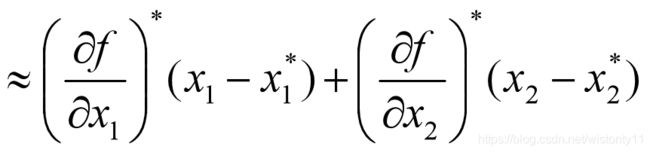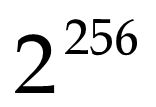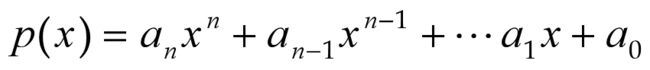《数值分析》李庆扬 01 误差分析
文章目录
- 0 内容串联
- 1. 误差种类
-
- 1.1 模型误差
- 1.2 截断误差
- 1.3 观测误差
- 1.4 舍入误差
- 1.5 数值分析误差对象
- 2. 一个例子讲解算法稳定和不稳定 123
- 3. 误差(*****)
-
- 3.1 绝对误差 e(x*)=x*-x
- 3.2 绝对误差限 |e(x*)|=|x*-x|≤ε(x*)
- 3.3 相对误差
- 3.4 相对误差限
- 3.5 一个例子来了解四个定义
- 4. 有效数字
-
- 4.1 定义2(非常重要)
- 4.2 定理1(非常重要)
- 5 数值计算的误差分析
-
- 5.1 一元
- 5.2 二元
- 6 四则运算中的稳定性问题
-
- 6.1 防止大暑防止大数吃小数
- 6.2 减法时应避免相近数相减
- 6.3 避免雄安舒做除数和大数做乘数
- 7 提高算法效率
- 7.1 尽量减少运算次数
- 8 课后练习(答案)
# 写于2020.12.29
# 教材《数值分析》 第五版 李庆扬 王能超 易大义
# 总结不易 望赞鼓励
0 内容串联
1. 误差分析
1. 误差种类
1.1 模型误差
用计算机解决科学计算问题首先要建立数学模型,它是对被描述的实际问题进行抽象、简化而得到的,因而是近似的.我们把数学模型与实际问题之间出现的这种误差称为模型误差.
1.2 截断误差
由实际问题建立起来的数学模型,在很多情况下要得到准确解是困难的,通常要用数值方法求它的近似解,例如常把无限的计算过程用有限的计算过程代替,这种模型的准确解和由数值方法求出的近似解之间的误差称为截断误差。因为截断误差是数值计算方法固有的,因此又称方法误差。
例如,函数可展开为无穷幂级数:

若取级数的起始若干项的部分和作为时函数的近似计算公式,例如取

则由于它的第四项和之后的各项都舍弃了,自然就产生了误差。这就是由于截断了无穷级数自第四项起的后段而产生的截断误差。
1.3 观测误差
观测误差,是指使用计量器具的过程中,由于观测者主观所引起的误差,比如读数,主观造成的
1.4 舍入误差
是指运算得到的近似值和精确值之间的差异。比如当用有限位数的浮点数来表示实数的时候(理论上存在无限位数的浮点数)就会产生舍入误差。舍入误差是量化误差的一种形式。 如果在一系列运算中的一步或者几步产生了舍入误差,在某些情况下,误差会随着运算次数增加而积累得很大,最终得出没有意义的运算结果。机器字长有限 会对超出的部分舍入
1.5 数值分析误差对象
模型误差 观测误差不是数值分析讨论的内容。计算方法主要研究截断误差和摄入误差在计算过程种的传播和计算结果的影响,以提高计算的精度。
2. 一个例子讲解算法稳定和不稳定 123
误差逐步递减, 这样的算法称为稳定的算法;
误差呈递增走势,造成这种情况的是不稳定的算法;
3. 误差(*****)
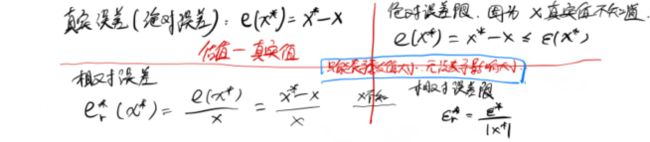
3.1 绝对误差 e(x*)=x*-x
- 估值与真实值之间的差
3.2 绝对误差限 |e(x*)|=|x*-x|≤ε(x*)
- 上面这个东西没法测 因为真实的x不知道;所以用了个ε(x*)
- e* 理论上讲是唯一确定的,可能取正,也可能取负。
- e* > 0 不唯一,当然 e* 越小越具有参考价值。
但是上面只能表示误差数值上的大小,无法表示误差对于这个真实值的影响
3.3 相对误差
e r ∗ ( x ∗ ) e_r^*(x*) er∗(x∗)= ( x ∗ − x ) x \frac{(x*-x)}{x} x(x∗−x)
也是具体不知道多少 因为x真正值不知道多少
3.4 相对误差限
ε r ∗ ( x ∗ ) ε_r^*(x*) εr∗(x∗)= ( x ∗ − x ) ∣ x ∗ ∣ \frac{(x*-x)}{|x^*|} ∣x∗∣(x∗−x)
3.5 一个例子来了解四个定义
对于x= 15±2 y=1000±5
那么:
近似值:
x* = 15;
y* = 1000;
绝对误差
e x e_x ex = 不知道
e y e_y ey = 不知道
绝对误差限
ε(x*)= 2
ε(y*)= 5
相对误差
e r ∗ e_r^* er∗(x*) = 不知道
e r ∗ e_r^* er∗(y*) = 不知道
相对误差限
ε r ∗ ε_r^* εr∗(x*) = 2/15
ε r ∗ ε_r^* εr∗(y*) = 5/1000
总结:虽然说y的误差数值上大,但是相对误差会比x小,也就是x误差影响会比y大
4. 有效数字
Π = 3.14 四位有效数字
Π = 3,14159 六位有效数字
4.1 定义2(非常重要)
|x-x*| <= 0.5 * 1 0 m 10^m 10m/ 1 0 n 10^n 10n
若x作为x的近似值,起雪堆u差的绝对值不超过莫一位数字的的半个单位,二该单位数字到x的第一位非零数字共有n位,则成用x近似x时具有n位有效数字,简称x有n位有效数字.
极其重要:意思就是当告诉你 x*有n位有效数字就是告诉

4.2 定理1(非常重要)
x的近似值x*可以表示成以下形式:
x* = ± 1 0 m 10^m 10m * 0. a 1 a_1 a1 a 2 a_2 a2… a n a_n an ; 其中 a 1 ≠ a_1\not= a1= 0
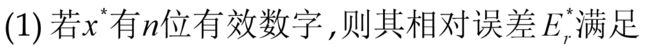
非常重要的结论:
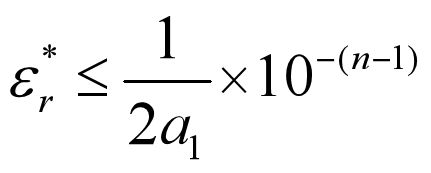
证明:
因为n为有效数字,所以可以写成:
- x* = ± 1 0 m 10^m 10m * 0. a 1 a_1 a1 a 2 a_2 a2… a n a_n an ;
- 其中 a 1 ≠ a_1\not= a1= 0
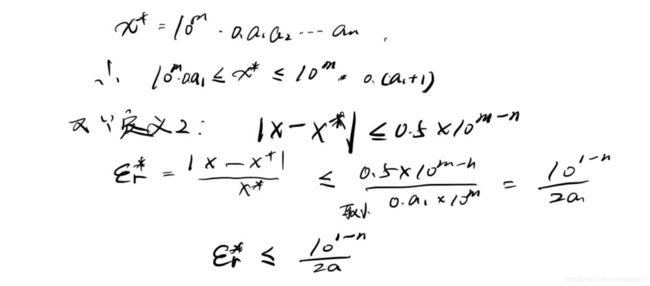
例:为使 的相对误差小于0.001%,至少应取几位有效数字?

5 数值计算的误差分析
5.1 一元
问题:对于 y = f (x),若用 x* 取代 x,将对y 产生什么影响?
-
e*(y) = f (x*) -f (x) = f ’(ξ)(x* - x)
-
e*(x) = x* - x
拉格朗日中值定理
中值定理是微积分学中的基本定理,由四部分组成。
内容是说一段连续光滑曲线中必然有一点,它的斜率与整段曲线平均斜率相同(严格的数学表达参见下文)。中值定理又称为微分学基本定理,拉格朗日定理,拉格朗日中值定理,以及有限改变量定理等。
如果函数 满足在闭区间[a,b]上连续;在开区间(a,b)内可导,那么在(a,b)内至少有一点 ,使等式
成立。
结论:x* 与 x 非常接近时,可认为 f ’(ξ ) ≈ f ’(x*) ,则有:|e*(y)| ≈ | f ’(x*)|·|e*(x)|
即:x产生的误差经过 f 作用后被放大/缩小了| f ’(x)|倍。故称| f ’(x*)|为放大因子 /* amplification factor / 或 绝对条件数 / absolute condition number */.
5.2 二元
6 四则运算中的稳定性问题
6.1 防止大暑防止大数吃小数
可能减轻误差方法:
① 相加时小的先相加再同大数加
② 如果是求根时x1算出来了,可以用x1*x2=c/a来算
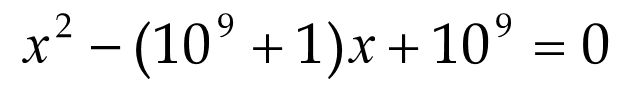
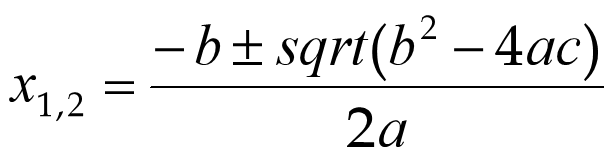
算出来x1= 1 0 9 10^9 109
如果依旧用求根公式来算 可能因为机器字长限制,x2= 0;
这里我们利用根的关系,x1*x2=c/a 求得x2 =1;
6.2 减法时应避免相近数相减
可能减轻误差方法:同等代换换成加法
6.3 避免雄安舒做除数和大数做乘数
在设计算法时候要尽量避免