<每日一题 / 每日刷题>LeetCode题目汇总Ⅰ
今天在公司和同事聊起了算法题,首先感到惊讶的是公司里还有每天刷题的人,然后我和他交流了几道链表题的解法,感觉很愉快。
我想起了我真正接触到leetcode的那一天起,就迷上了解题,每天都抽出很多时间来学习数据结构与算法并且刷题。然而,后面要准备很多面试的知识,就停止了刷题……
刷题的那段时光无疑是快乐的,那时候每天都能学到很多的新知识,专心刷题,进入专注状态,没有分心于简历和面试什么的。
看到同事刷了两百多道题,我突然又想重新开始刷题,至少每天一道。
文章目录
- 2020-12-16
-
- 1.单词规律(每日一题)
- 2.删除链表的节点
- 3.删除链表中的节点
- 2020-12-17
-
- 1.买卖股票的最佳时机含手续费(每日一题)
- 2020-12-18
-
- 1.找不同(每日一题)
- 2.最佳买卖股票时机含冷冻期
- 2020-12-19
-
- 1.旋转图像(每日一题)
- 2.Z字形变换
- 2020-12-20
-
- 1.去除重复字母(每日一题)
- 2.字符串转换整数(atio)
- 2020-12-21
-
- 1.使用最小花费爬楼梯(每日一题)
- 2.寻找两个正序数组的中位数
- 3.回文数
- 4.两数相除
- 2020-12-22
-
- 1.二叉树的锯齿形层序遍历(每日一题)
- 2.
- 2020-12-23
-
- 1.字符串中的第一个唯一字符
- 2.单调递增的数字(12-15每日一题)
- 2020-12-24
-
- 1.分发糖果(每日一题)
- 2020-12-25
-
- 1.分发饼干(每日一题)
- 2020-12-26
-
- 1.最大矩形(每日一题)
- 2020-12-27
-
- 1.同构字符串(每日一题)
- 2020-12-28
-
- 1.买卖股票的最佳时机 IV(每日一题)
- 2.买卖股票的最佳时机 III
- 2020-12-29
-
- 1. 按要求补齐数组(每日一题)
- 2.柱状图中最大的矩形
- 3.接雨水
2020-12-16
1.单词规律(每日一题)
class Solution {
public boolean wordPattern(String pattern, String s) {
Map map = new HashMap<>();
String[] strs = s.split(" ");
if (pattern.length() != strs.length) {
return false;
}
for(int i = 0; i < strs.length; i++) {
if (!map.containsKey(pattern.charAt(i)) && !map.containsValue(strs[i])) {
map.put(pattern.charAt(i), strs[i]);
} else {
// if (map.get(pattern.charAt(i)) != strs[i]) {
if (map.get(pattern.charAt(i)) == null || !map.get(pattern.charAt(i)).equals(strs[i])) {
return false;
}
}
}
return true;
}
}
2.删除链表的节点
public ListNode deleteNode(ListNode head, int val) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode cur = dummyHead;
while (cur != null && cur.next != null) {
if (cur.next.val == val) {
cur.next = cur.next.next;
}
cur = cur.next;
}
return dummyHead.next;
}
法2:头节点先处理法
public ListNode deleteNode(ListNode head, int val) {
if (head.val == val) {
return head.next;
}
ListNode cur = head;
while (cur != null && cur.next != null) {
if (cur.next.val == val) {
cur.next = cur.next.next;
}
cur = cur.next;
}
return head;
}
法3:递归
public ListNode deleteNode(ListNode head, int val) {
if (head == null) {
return null;
}
if (head.val == val) {
return head.next;
}
head.next = deleteNode(head.next, val);
return head;
}
链表的递归似乎比二叉树难理解,但我通常把链表当成一个极不平衡的二叉树来理解,因为链表只有一条链路一直.next连下去嘛(不知道这样理解对不对),链表head相当于二叉树root。还记得二叉搜索树的删除节点吗?那道题写起来其实挺繁杂的,链表删除节点可以看成它的简化版。
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (key < root.val) {
// 待删除节点在左子树中
root.left = deleteNode(root.left, key);
// return root;
} else if (key > root.val) {
// 待删除节点在右子树中
root.right = deleteNode(root.right, key);
// return root;
} else {
// key == root.val,root 为待删除节点
if (root.left == null) {
// 返回右子树作为新的根
return root.right;
} else if (root.right == null) {
// 返回左子树作为新的根
return root.left;
} else {
// 左右子树都存在,返回后继节点(右子树最左叶子)作为新的根
TreeNode successor = min(root.right);
successor.right = deleteMin(root.right);
successor.left = root.left;
return successor;
}
}
return root;
}
private TreeNode min(TreeNode node) {
if (node.left == null) {
return node;
}
return min(node.left);
}
private TreeNode deleteMin(TreeNode node) {
if (node.left == null) {
return node.right;
}
node.left = deleteMin(node.left);
return node;
}
}
3.删除链表中的节点
public void deleteNode(ListNode node) {
node.val = node.next.val;
node.next = node.next.next;
}
时间空间复杂度都是O(1)。
差不多一个月没刷过题了,重新做题感觉还行,很多东西都没忘掉,看来以前的高强度刷题还是有效的。一个晚上的时间很快就过去了,我得留点时间给陀思妥耶夫斯基的《死屋手记》,晚安。
2020-12-17
1.买卖股票的最佳时机含手续费(每日一题)
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
dp[i]只从dp[i-1]转移得到
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
int[] dp = new int[2];
dp[0] = 0;
dp[1] = -prices[0];
for (int i = 1; i < n; i++) {
int tmp = dp[0];
dp[0] = Math.max(dp[0], dp[1] + prices[i] - fee);
dp[1] = Math.max(dp[1], tmp - prices[i]);
}
return dp[0];
}
2020-12-18
1.找不同(每日一题)
public char findTheDifference(String s, String t) {
int[] ca = new int[26];
for (int i = 0; i < s.length(); i++) {
ca[s.charAt(i) - 'a']++;
}
for (int i = 0; i < t.length(); i++) {
if (--ca[t.charAt(i) - 'a'] < 0) {
return t.charAt(i);
}
}
return t.charAt(0);
}
法2:位运算
一个集合比另一个集合多一个数,异或运算是个很不错的解决方案。
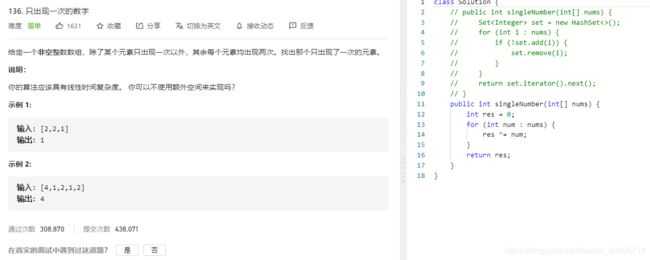
public char findTheDifference(String s, String t) {
int ret = 0;
for (char ch : s.toCharArray()) {
ret ^= ch;
}
for (char ch : t.toCharArray()) {
ret ^= ch;
}
return (char)ret;
}
2.最佳买卖股票时机含冷冻期
public int maxProfit(int[] prices) {
int n = prices.length;
if (n == 0) {
return 0;
}
int[][] dp = new int[n][3];
dp[0][0] = -prices[0]; // 持有
dp[0][1] = 0; // 不持有且冷冻
dp[0][2] = 0; // 不持有不冷冻
for (int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]);
dp[i][1] = dp[i - 1][0] + prices[i];
dp[i][2] = Math.max(dp[i - 1][1], dp[i - 1][2]);
}
return Math.max(dp[n - 1][1], dp[n - 1][2]);
}
2020-12-19
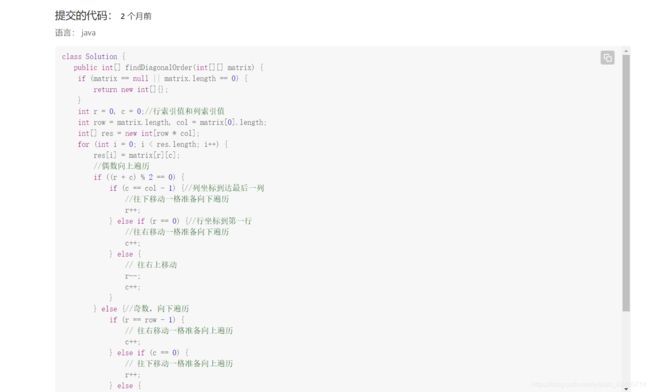
1.旋转图像(每日一题)
public void rotate(int[][] matrix) {
int n = matrix.length;
// 绕中间行翻转
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - i][j];
matrix[n - 1 - i][j] = tmp;
}
}
// 绕正对角线翻转
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j < n; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
}
}
我记得做过这道题,力扣是不是有一些同样的题目然后改个标题啊。
2.Z字形变换
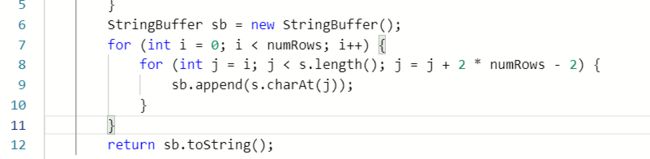
先打印那些一列列整列的值,然后在相应位置插值。(注:只有不是首尾行的才需要插值。)

法1:
public String convert(String s, int numRows) {
if (numRows <= 1) {
return s;
}
StringBuffer sb = new StringBuffer();
for (int i = 0; i < numRows; i++) {
for (int j = i; j < s.length(); j = j + 2 * numRows - 2) {
// if (i != 0 && i != numRows - 1 && j != i) {
// sb.append(s.charAt(j - 2 * i));
// }
sb.append(s.charAt(j));
if (i !=0 && i != numRows - 1 && j + 2 * (numRows - i - 1) < s.length()) {
sb.append(s.charAt(j + 2 * (numRows - i - 1)));
}
}
}
return sb.toString();
}
法2:
法2我称之为模拟法,这个思路主要来自之前做过的对角线遍历那道题。只不过这道题的模拟显然简单很多。。

public String convert(String s, int numRows) {
if (numRows <= 1) {
return s;
}
List<StringBuffer> sbList = new ArrayList<>();
for (int i = 0; i < numRows; i++) {
sbList.add(new StringBuffer());
}
boolean UpFlag = false;
int row = 0;
for (int i = 0; i < s.length(); i++) {
sbList.get(row).append(s.charAt(i));
if (UpFlag) {
row--;
} else {
row++;
}
if (row == numRows - 1 || row == 0) {
UpFlag = !UpFlag;
}
}
StringBuffer res = new StringBuffer();
for (StringBuffer sb : sbList) {
res.append(sb);
}
return res.toString();
}
2020-12-20
1.去除重复字母(每日一题)
public String removeDuplicateLetters(String s) {
if (s == null || s.length() == 0) {
return "";
}
Deque<Character> deque = new LinkedList<>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (deque.contains(ch)) {
continue;
}
while (!deque.isEmpty() && ch < deque.peekLast() && s.indexOf(deque.peekLast(), i) != -1) {
deque.pollLast();
}
deque.offerLast(ch);
}
StringBuilder res = new StringBuilder();
while (!deque.isEmpty()) {
res.append(deque.pollFirst());
}
return res.toString();
}
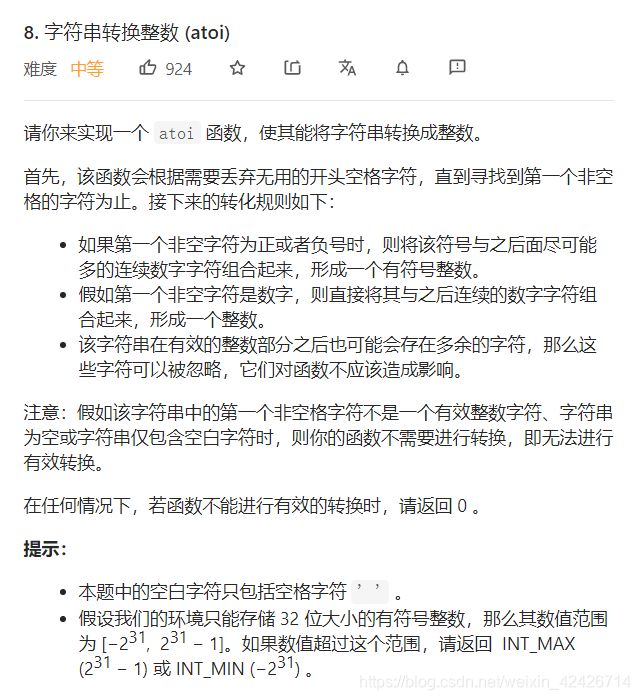
2.字符串转换整数(atio)
public int myAtoi(String str) {
char[] chars = str.toCharArray();
int n = chars.length;
int idx = 0;
while (idx < n && chars[idx] == ' ') {
idx++;
}
if (idx == n) {
return 0;
}
boolean negative = false;
if (chars[idx] == '-') {
negative = true;
idx++;
} else if (chars[idx] == '+') {
idx++;
} else if (!Character.isDigit(chars[idx])) {
return 0;
}
int ans = 0;
while (idx < n && Character.isDigit(chars[idx])) {
int digit = chars[idx] - '0';
if (ans > (Integer.MAX_VALUE - digit) / 10) {
return negative? Integer.MIN_VALUE : Integer.MAX_VALUE;
}
ans = ans * 10 + digit;
idx++;
}
return negative? -ans : ans;
}
2020-12-21
1.使用最小花费爬楼梯(每日一题)
public int minCostClimbingStairs(int[] cost) {
int n = cost.length;
for (int i = 2; i < n; i++) {
// cost[i] = cost[i] + Math.min(cost[i - 2], cost[i - 1]);
cost[i] += Math.min(cost[i - 2], cost[i - 1]);
}
return Math.min(cost[n - 2], cost[n - 1]);
}
法2:dp
public int minCostClimbingStairs(int[] cost) {
int n = cost.length;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i < n + 1; i++) {
dp[i] = Math.min(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
}
return dp[n];
}
2.寻找两个正序数组的中位数
法1:调api
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int n = nums1.length + nums2.length;
int[] nums = new int[n];
System.arraycopy(nums1, 0, nums, 0, nums1.length);
System.arraycopy(nums2, 0, nums, nums1.length, nums2.length);
Arrays.sort(nums);
return n % 2 == 1 ? nums[(n - 1) / 2] : (double)(nums[(n - 1) / 2] + nums[n / 2]) / 2;
}
法2:二分法
参考了官方题解及评论区,边界条件有点难想。
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int n1 = nums1.length;
int n2 = nums2.length;
int left = (n1 + n2 + 1) / 2;
int right = (n1 + n2 + 2) / 2;
return (getKth(nums1, 0, nums2, 0, left) + getKth(nums1, 0, nums2, 0, right)) / 2.0;
}
private int getKth(int[] nums1, int i, int[] nums2, int j, int k) {
int n1 = nums1.length;
int n2 = nums2.length;
if (i >= nums1.length) {
return nums2[j + k - 1];
}
if (j >= nums2.length) {
return nums1[i + k - 1];
}
if (k == 1) {
return Math.min(nums1[i], nums2[j]);
}
int m1 = (i + k / 2 - 1 < n1) ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;
int m2 = (j + k / 2 - 1 < n2) ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;
if (m1 < m2) {
return getKth(nums1, i + k / 2, nums2, j, k - k / 2);
} else {
return getKth(nums1, i, nums2, j + k / 2, k - k / 2);
}
}
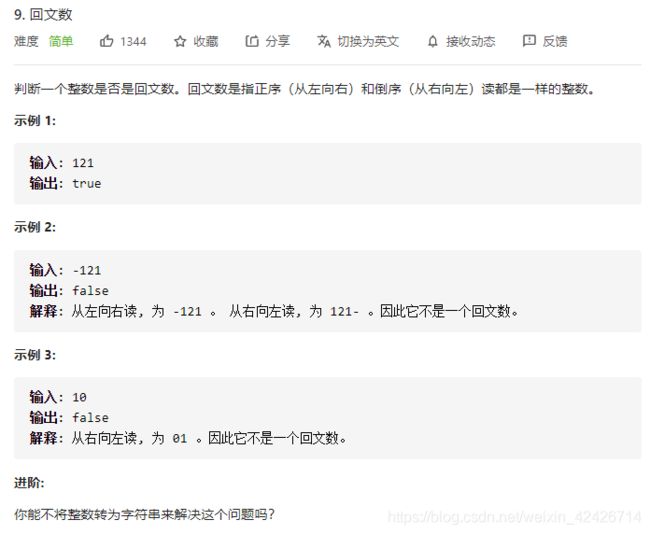
3.回文数
public boolean isPalindrome(int x) {
if (x < 0) {
return false;
}
int res = 0;
int y = x;
while (y != 0) {
int tmp = y % 10;
res = res * 10 + tmp;
y /= 10;
}
return x == res;
}
4.两数相除
public int divide(int dividend, int divisor) {
if (dividend == 0) {
return 0;
}
if (dividend == Integer.MIN_VALUE && divisor == -1) {
return Integer.MAX_VALUE;
}
boolean negative = (dividend ^ divisor) < 0;
long a = Math.abs((long)dividend);
long b = Math.abs((long)divisor);
int res = 0;
for (int i = 31; i >= 0; i--) {
if ((a >> i) >= b) {
res = res + (1 << i);
a = a - (b << i);
}
}
return negative ? -res : res;
}
2020-12-22
1.二叉树的锯齿形层序遍历(每日一题)
思路很简单,奇数层用Collections类的reverse方法反转列表元素即可。
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
if (root == null) {
return new ArrayList();
}
List<List<Integer>> ans = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int level = 0;
while (!queue.isEmpty()) {
List<Integer> res = new ArrayList<>();
int n = queue.size();
for (int i = 0; i < n; i++) {
TreeNode cur = queue.poll();
res.add(cur.val);
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
if (level % 2 != 0) {
Collections.reverse(res);
}
ans.add(res);
level++;
}
return ans;
}
2.
2020-12-23
1.字符串中的第一个唯一字符
public int firstUniqChar(String s) {
if (s == null || s.length() == 0) {
return -1;
}
for (int i = 0; i < s.length(); i++) {
for (int j = 0; j < s.length(); j++) {
if (i != j && s.charAt(i) == s.charAt(j)) {
break;
}
if (j == s.length() - 1) {
return i;
}
}
}
return -1;
}
法2:哈希表
public int firstUniqChar(String s) {
if (s == null || s.length() == 0) {
return -1;
}
Map<Character, Integer> map = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
map.put(c, map.getOrDefault(c, 0) + 1);
}
for (int i = 0; i < s.length(); i++) {
if (map.get(s.charAt(i)) == 1) {
return i;
}
}
return -1;
}
法3:new int[26]法
public int firstUniqChar(String s) {
if (s == null || s.length() == 0) {
return -1;
}
int[] ca = new int[26];
for (int i = 0; i < s.length(); i++) {
ca[s.charAt(i) - 'a']++;
}
for (int i = 0; i < s.length(); i++) {
if (ca[s.charAt(i) - 'a'] == 1) {
return i;
}
}
return -1;
}
2.单调递增的数字(12-15每日一题)
public int monotoneIncreasingDigits(int N) {
char[] ca = Integer.toString(N).toCharArray();
for (int i = 0; i < ca.length - 1; i++) {
if (ca[i] > ca[i + 1]) {
while (i > 0 && ca[i] == ca[i - 1]) {
i--;
}
ca[i] -= 1;
for (int j = i + 1; j < ca.length; j++) {
ca[j] = '9';
}
}
}
return Integer.valueOf(new String(ca));
}
2020-12-24
1.分发糖果(每日一题)
最简单的方法是构造一个数组存放每个孩子的糖果数目,然后遍历求和。
public int candy(int[] ratings) {
if (ratings == null || ratings.length == 0) {
return 0;
}
int n = ratings.length;
int[] nums = new int[n];
for (int i = 0; i < n - 1; i++) {
if (ratings[i + 1] > ratings[i]) {
nums[i + 1] = nums[i] + 1;
}
}
for (int i = n - 1; i > 0; i--) {
if (ratings[i - 1] > ratings[i]) {
nums[i - 1] = Math.max(nums[i - 1], nums[i] + 1);
}
}
int res = n;
for (int i : nums) {
res += i;
}
return res;
}
2020-12-25
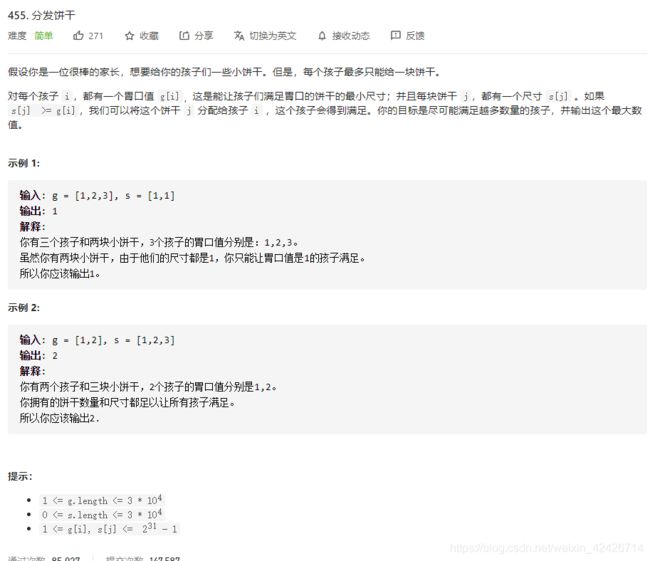
1.分发饼干(每日一题)
public int findContentChildren(int[] g, int[] s) {
int res = 0;
Arrays.sort(g);
Arrays.sort(s);
int n1 = g.length;
int n2 = s.length;
int i = 0;
int j = 0;
while (i < n1 && j < n2) {
if (s[j++] >= g[i]) {
res++;
i++;
}
}
return res;
}
2020-12-26
1.最大矩形(每日一题)
public int maximalRectangle(char[][] matrix) {
int m = matrix.length;
if (m == 0) {
return 0;
}
int n = matrix[0].length;
int[][] nums = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
nums[i][j] = j == 0 ? 1 : nums[i][j - 1] + 1;
}
}
}
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '0') {
continue;
}
int width = nums[i][j];
int area = width;
for (int k = i - 1; k >= 0; k--) {
width = Math.min(width, nums[k][j]);
area = Math.max(area, (i - k + 1) * width);
}
res = Math.max(res, area);
}
}
return res;
}
2020-12-27
1.同构字符串(每日一题)
public boolean isIsomorphic(String s, String t) {
Map<Character, Character> map = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
if (!map.containsKey(s.charAt(i))) {
if (map.containsValue(t.charAt(i))) {
return false;
}
map.put(s.charAt(i), t.charAt(i));
} else {
if (map.get(s.charAt(i)) != t.charAt(i)) {
return false;
}
}
}
return true;
}
2020-12-28
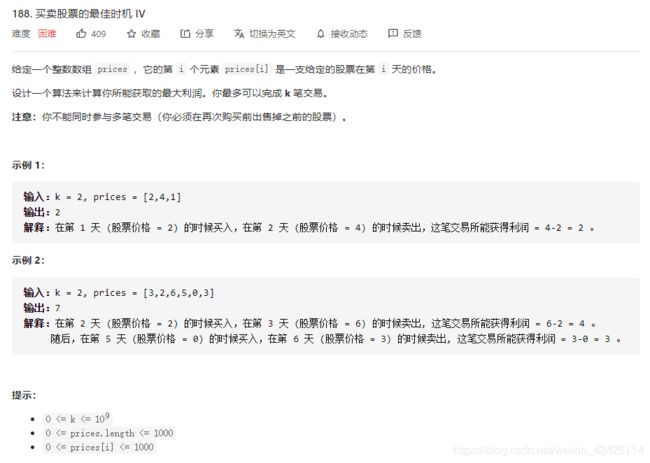
1.买卖股票的最佳时机 IV(每日一题)
public int maxProfit(int k, int[] prices) {
if (prices == null || prices.length == 0) {
return 0;
}
int[][][] dp = new int[prices.length][k + 1][2];
// dp[0][0][0] = 0;
// dp[0][0][1] = -prices[0];
for (int i = 0; i < prices.length; i++) {
for (int j = 1; j < k + 1; j++) {
if (i == 0) {
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
} else {
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
}
return dp[prices.length - 1][k][0];
}
2.买卖股票的最佳时机 III
public int maxProfit(int[] prices) {
if (prices == null || prices.length ==0) {
return 0;
}
int n = prices.length;
int[][][] dp = new int[n][3][2];
for (int i = 0; i < n; i++) {
for (int j = 1; j < 3; j++) {
if (i == 0) {
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
} else {
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
}
return dp[n - 1][2][0];
}
2020-12-29
1. 按要求补齐数组(每日一题)
public int minPatches(int[] nums, int n) {
// int tmp = 0;
long tmp = 0;
int res = 0;
int len = nums.length;
int idx = 0;
while (tmp < n) {
if (idx < len && nums[idx] <= tmp + 1) {
tmp += nums[idx++];
} else {
res++;
tmp += tmp + 1;
}
}
return res;
}
2.柱状图中最大的矩形
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) {
return 0;
}
int res = 0;
int n = heights.length;
for (int i = 0; i < n; i++) {
int minValue = Integer.MAX_VALUE;
for (int j = i; j < n; j++) {
minValue = Math.min(minValue, heights[j]);
res = Math.max(res, minValue * (j - i + 1));
}
}
return res;
}
法2:单调栈
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) {
return 0;
}
int[] nums = new int[heights.length + 2];
System.arraycopy(heights, 0, nums, 1, heights.length);
Deque<Integer> deque = new LinkedList<>();
int res = 0;
for (int i = 0; i < nums.length; i++) {
while (!deque.isEmpty() && nums[i] < nums[deque.peekLast()]) {
int height = nums[deque.pollLast()];
res = Math.max(res, (i - deque.peekLast() - 1) * height);
}
deque.offerLast(i);
}
return res;
}
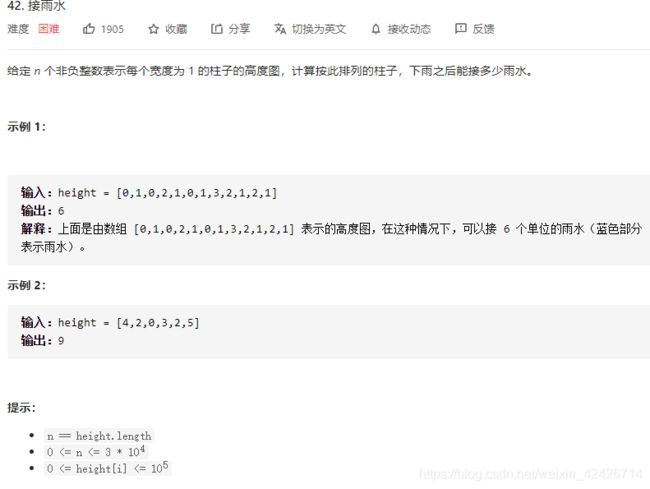
3.接雨水
public int trap(int[] height) {
if (height == null || height.length < 3) {
return 0;
}
int res = 0;
for (int i = 1; i < height.length - 1; i++) {
int left = 0;
int right = 0;
for (int j = i; j < height.length; j++) {
right = Math.max(right, height[j]);
}
for (int j = i; j >= 0; j--) {
left = Math.max(left, height[j]);
}
res += Math.min(right, left) - height[i];
}
return res;
}