十五数码——原理及实现(C语言)
目录
1、问题描述
2、原理及方法
2.1 启发式图搜索
2.1.1 启发式图搜索
2.1.2 启发式搜索算法A
2.2 A*
3、算法设计
3.1 数据结构
3.1.1 结构体
3.1.2 数组
3.1.3 链表
3.2 函数
3.2.1 寻找0点位置
3.2.2 比较函数
3.2.3 移动函数
3.2.4 复制函数
3.2.5 输出函数
3.2.6 计算评价函数
3.3 循环
3.4 最小状态min
4、实验结果
1、问题描述
设计一个启发函数,利用A*算法求解15数码问题。
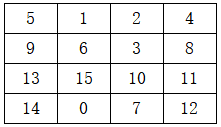
初始状态:
目标状态:
2、原理及方法
2.1 启发式图搜索
2.1.1 启发式图搜索
1、概念
启发式搜索时利用问题拥有的启发信息来引导搜索,达到减少搜索范围,降低问题复杂度的目的。这种利用启发信息的搜索过程称为启发式搜索方式。
2、核心思想
利用所处理问题的启发信息引导搜索。
3、目的
减少搜索范围,降低问题复杂度。
2.1.2 启发式搜索算法A
1、概念
启发式搜索算法A,一般简称为A算法,是一种典型的启发式搜索算法。
2、基本思想
定义一个评价函数f,对当前的搜索状态进行评估,找出一个最有希望的结点来拓展。
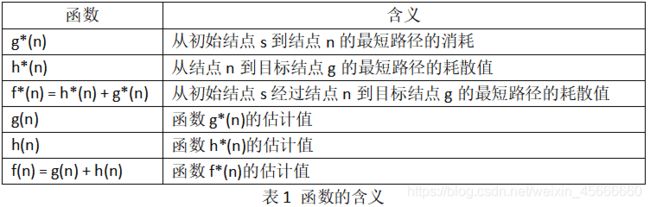
3、评价函数
f(n) = g(n) + h(n)
其中,n是被评价的结点。
具体函数含义如下表所示:
4、过程
A算法就是利用预测,来达到有效搜索的目的。它每次按照f(n)值的大小对OPEN表中的元素进行排序,f值小的结点放在前面,而f值大的结点则被放在OPEN表的后面,这样每次扩展结点时,总是选择当前f值最小的结点来优先拓展。
- OPEN:=(s),f(s):=g(s)+h(s);
- LOOP: IF OPEN=( ) THEN EXIT(FAIL);
- n:=FIRST(OPEN);
- IF GOAL (n) THEN EXIT(SUCCESS);
- REMOVE (n, OPEN), ADD(n, CLOSED);
- EXPAND(n)→ (mi),把mi作为n的后继节点添入G,并计算 f(n-mi)=g(n-mi)+h(mi);
ADD (mj, OPEN),
IF f(n-mk) < f(mk) THEN f(mk):=f(n-mk),
IF f(n-ml) < f(ml) THEN f(ml):=f(n-ml),ADD(ml,OPEN);
- OPEN 中的节点按 f 值从小到大排序;
- GO LOOP;
5、算法说明
- A 算法由一般的图搜索算法改变而成;
- 控制策略:按照 f(n)值递增的顺序对 OPEN 中的元素进行排序,f(n)值小的节点排在前面,大的放在 OPEN 表的后面。
- 效果:每次扩展节点时,优先选择当前f(n)值最小的节点来扩展。
- 结论:算法 A 是一个好的优先搜索策略。
6、搜索策略
- 扩展n后新生成的子节点m1({mj})、m2({mk})、m3({ml})分别计算其评价函数值:
f(m1)=g(m1)+h(m1);
f(n-m2)=g(n-m2)+h(m2);
f(n-m3)=g(n-m3)+h(m3);
- 按第6步比较不同路径的耗散值并进行相应的指针修正。
2.2 A*
1、概念
在算法A中,当 h(n) ≤ h*(n) 时,称其为A*算法。
2、性质
- 完备性:如果问题有解,则算法一定能找到解。
- 可采纳性:如果问题有解,则算法一定能找到最佳解。即算法总能找到一条从 S 到目标节点的最佳路径。
- 最优性:设A1和A2为某问题求解的两个A* 算法,若对所有非目标节点均有 h1(n) < h2(n) ≤ h*(n) 则算法 A1展开的节点数目至少和A2一样多。
3、结论
通过A*算法的性质的证明,可得到几个有助于理解A*算法的结论:
- A*算法结束前,OPEN表中必存在f(n) ≤ f*(S)的节点(n是在最佳路径上的节点)。
- OPEN表上任一具有 f(n) ≤ f*(S)的节点n,最终都将被A*选作扩展的节点。
- A*选作扩展的任一节点,有 f(n) ≤ f*(S)。
4、不足
- 存在的问题: 如果用扩展节点数作为评价搜索效率的准则,那么可以发现A算法第6步中,对CLOSED表中ml类节点要重新放回OPEN表中的操作,将引起多次扩展同一节点的可能。
- 不良结果: 即使问题所包含的节点数少,但重复扩展某些节点,也将导致搜索效率下降。
5、改进
- 对h加以限制,使得第一次扩展一个节点时,就找到了从s到该节点的最短路径。
- 对算法加以改进,避免或减少节点的多次扩展。
6、改进后的算法过程
- OPEN:=(s),f(s):=g(s)+h(s)= h(s),fm:=0;
- LOOP:IF OPEN=() THEN EXIT (FAIL);
- NEST:= { ni |f (ni) < fm }; * NEST给出了OPEN表中满足 f < fm 的节点集合。fm为处理过的节点中最大的f值*。(划分OPEN表)
IF NEST ≠ () THEN n:= ni (min (gi)) ELSE n:=FIRST (OPEN),fm =f(n);* NEST不空时,取其中 g(n) 的最小者作为当前要扩展的节点,否则取 OPEN 的第一个为当前要扩展的节点* (保证搜索效率)
- IF GOAL (n) THEN EXIT(SUCCESS);
- REMOVE (n, OPEN), ADD(n, CLOSED);
- EXPAND(n)→ (mi),把mi作为n的后继节点添入G,并计算 f(n-mi)=g(n-mi)+h(mi);
ADD (mj, OPEN),
IF f(n-mk) < f(mk) THEN f(mk):=f(n-mk),
IF f(n-ml) < f(ml) THEN f(ml):=f(n-ml),ADD(ml,OPEN);
- OPEN 中的节点按 f 值从小到大排序;
- GO LOOP;
3、算法设计
3.1 数据结构
3.1.1 结构体
1、概念
在C语言中,结构体(struct)指的是一种数据结构,是C语言中聚合数据类型(aggregate data type)的一类。结构体可以被声明为变量、指针或数组等,用以实现较复杂的数据结构。结构体同时也是一些元素的集合,这些元素称为结构体的成员(member),且这些成员可以为不同的类型,成员一般用名字访问。
2、定义
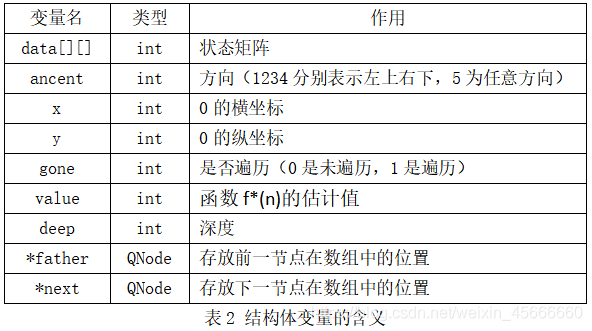
typedef struct QNode {
int data[N][N];
int ancent;
int x;
int y;
int gone;
int value;
int deep;
struct QNode* father;
struct QNode* next;
}QNode, *QueuePtr;我们定义了一个名为QNode的结构体,结构体中的变量的作用及类型如下表所示:
在这里我们设置评价函数为:f(n) = d(n) + p(n)。
其中,d(n)代表结点的深度,取g(n) = d(n)表示讨论单位耗散的情况;取h(n) = p(n)表示以“不在位”的每一个将牌与其目标位置之间的距离的总和作为启发函数的度量。
我们的距离采用的是曼哈顿距离。曼哈顿距离,就是表示两个点在标准坐标系上的绝对轴距之和。
3.1.2 数组
1、概念
在C语言中,数组属于构造数据类型。一个数组可以分解为多个数组元素,这些数组元素可以是基本数据类型或是构造类型。因此按数组元素的类型不同,数组又可分为数值数组、字符数组、指针数组、结构数组等各种类别。
2、定义
int A[N][N] = {
{5,1,2,4},
{9,6,3,8},
{13,15,10,11},
{14,0,7,12}
};
int B[N][N] = {
{1,2,3,4},
{5,6,7,8},
{9,10,11,12},
{13,14,15,0}
};我们定义了两个4*4的二位数组,A,B。分别用来存储初始状态和目标状态。如下表所示:
3.1.3 链表
1、概念
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。相比于线性表顺序结构,操作复杂。
链表具有单链表、循环单链表、双链表、循环双链表。在这里我们使用的是双链表。
2、定义
typedef struct {
QueuePtr head;
QueuePtr rear;
}LinkQueue;其中head是头结点,rear是尾结点。
3.2 函数
3.2.1 寻找0点位置
bool begin_opint() {
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
if (A[i][j] == 0) {
x = i; y = j;
return true;
}
}
}
return false;
}3.2.2 比较函数
bool compare(int a[N][N]) {
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
if (a[i][j] != B[i][j])
return false;
}
}
return true;
}传入的a矩阵,即当前状态的矩阵同目标矩阵B进行比较。若相等,返回true,否则,返回false。
3.2.3 移动函数
针对十五数码问题,0位于不同位置的移动是不同的,如下图所示:
其中,1代表不能向上移,2不能向右移,3不能向下移,4不能向左移。以向左移动为例。
向左移动:
bool moveleft(int a[N][N], QueuePtr * b, int x, int y) {
int k, i, j;
if (y == 0)
return false;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
(*b)->data[i][j] = a[i][j];
}
k = (*b)->data[x][y];
(*b)->data[x][y] = (*b)->data[x][y - 1];
(*b)->data[x][y - 1] = k;
(*b)->x = x;
(*b)->y = y - 1;
return true;
}当0位于数组的第一行时,不可以向上移,即y = 0时,返回false。
3.2.4 复制函数
bool copy(QueuePtr * a) {
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
(*a)->data[i][j] = A[i][j];
}
return true;
}将初始状态A矩阵复制到当前状态a矩阵中。
3.2.5 输出函数
void output(QueuePtr * p) {
int i, j;
long int n = 0;
for (; (*p)->father != NULL; (*p) = (*p)->father, n++) {
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
printf(" %d", (*p)->data[i][j]);
}printf("\n");
}printf("\n");
}
printf("step is %d\n", n - 1);
}若当前状态和目标状态相同,则输出。
3.2.6 计算评价函数
int getvalue(QueuePtr * p) {
int count = 0;
bool test = true;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
test = true;
for (int k = 0; k < N; k++) {
for (int l = 0; l < N; l++) {
if ((i != (*p)->x || j != (*p)->y) && (*p)->data[i][j] == B[k][l]) {
count = count + abs(i - k) + abs(j - l);
test = false;
}
if (test == false) break;
}
if (test == false) break;
}
}
}
count = count + (*p)->deep;
return count;
}评价函数为:f(n) = d(n) + p(n)。
其中,d(n)代表结点的深度,(*p)->deep;取h(n) = p(n)表示以“不在位”的每一个将牌与其目标位置之间的距离的总和作为启发函数的度量,count = count + abs(i - k) + abs(j - l);最后求其和:count = count + (*p)->deep。
3.3 循环
1、switch格式
switch(值){
case 值1:
代码
break;
case 值2:
代码
break;
default:
代码
break;
}
2、switch原理
(1) 找case的值 匹配到进入case执行代码,找break;
(2) 若没找到,找下一个case,如果都没找到就找default,进行default代码,找break;
(3) 若没break,进入下一个case或default找break,直到最后。
3、代码
switch (min->ancent) {
case 1:p = (QueuePtr)malloc(sizeof(QNode));
if (moveleft(min->data, &p, min->x, min->y)) {
...
}
case 2:p = (QueuePtr)malloc(sizeof(QNode));
if (moveleft(min->data, &p, min->x, min->y)) {
...
}
case 3:p = (QueuePtr)malloc(sizeof(QNode));
if (moveleft(min->data, &p, min->x, min->y)) {
...
}
case 4:p = (QueuePtr)malloc(sizeof(QNode));
if (moveup(min->data, &p, min->x, min->y)) {
...
}
default:p = (QueuePtr)malloc(sizeof(QNode));
if (moveleft(min->data, &p, min->x, min->y)) {
...
}min->ancent表示最小状态上一次移动的方向,即当前状态不可移动上一次移动方向的反方向。
当min->ancent = 1时,表示祖先结点从右边来,即不可再向右移动;当min->ancent = 2时,祖先结点从下边来,即不可再向下移动;当min->ancent = 3时,表示祖先结点从左边来,即不可再向左移动;当min->ancent = 4时,表示祖先结点从上面来,即不可再向上移动;当min->ancent ≠ 1,2,3,4时,表示当前状态为初始状态,祖先为空,因此任意方向均可。当前状态p插入到OPEN表的尾部。
3.4 最小状态min
for (min = q = open.head->next; q != NULL; q = q->next) {
if (q->value <= min->value && q->gone == 0) {
min = q;
break;
}
}
}min为最小状态,通过遍历OPEN表寻找最小状态。
min->father->next = min->next;
min->next = closed->next;
closed->next = min;
在open表中删除找到的最小态,并将最小态min插入到CLOSED表头。
4、实验结果
所有结果均为逆序,因为每次输出的均是当前状态的父节点。
1、目标状态
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 0
2、中间状态
1 2 3 4
5 6 7 8
9 10 11 0
13 14 15 12
1 2 3 4
5 6 7 8
9 10 0 11
13 14 15 12
1 2 3 4
5 6 0 8
9 10 7 11
13 14 15 12
1 2 0 4
5 6 3 8
9 10 7 11
13 14 15 12
1 0 2 4
5 6 3 8
9 10 7 11
13 14 15 12
0 1 2 4
5 6 3 8
9 10 7 11
13 14 15 12
5 1 2 4
0 6 3 8
9 10 7 11
13 14 15 12
5 1 2 4
9 6 3 8
0 10 7 11
13 14 15 12
5 1 2 4
9 6 3 8
13 10 7 11
0 14 15 12
5 1 2 4
9 6 3 8
13 10 7 11
14 0 15 12
5 1 2 4
9 6 3 8
13 10 7 11
14 15 0 12
5 1 2 4
9 6 3 8
13 10 0 11
14 15 7 12
5 1 2 4
9 6 3 8
13 0 10 11
14 15 7 12
3、初始状态
5 1 2 4
9 6 3 8
13 15 10 11
14 0 7 12
4、代价
step is 14