一篇带你搞透回溯算法

回溯算法应用场合

回溯算法和递归算法一般同时出现，一般递归算法的下面就是回溯的逻辑。
一般说递归函数，其实就是回溯函数。回溯一般不会单独出现。
回溯法其实是一个纯暴力的搜索算法。有些问题用for循环搜索不出来，必须用回溯算法。以下几种问题必须用回溯。

• 组合问题。N个数里面按一定规则找出k个数的集合。如给定一个数组[1234]，从中找出大小为2的集合，结果是12,13,14,23,24,34
• 切割问题。一个字符串按一定规则有几种切割方式。如给定一个字符串，求如何切割保证子串都是回文子串。
• 子集问题。一个N个数的集合里有多少符合条件的子集。如求出数组【1234】的子集，答案是1,2，3,4，12,13,14,23,24,34，123,124,234,1234。
• 排列问题。N个数按一定规则全排列，有几种排列方式。如果一个是12，求它的排列，答案是12，21。。组合强调元素是什么，不关心顺序，排列关心。
• 棋盘问题。如 N皇后，解数独。

回溯算法的理解

回溯算法可以抽象成一个树形结构。
回溯算法前面有递归，递归都是有终止条件的。
回溯是递归的副产品，只要有递归就会有回溯」，所以回溯法也经常和二叉树遍历，深度优先搜索混在一起，因为这两种方式都是用了递归。

如图所示，树的宽度表示集合的大小，一般用for循环遍历，树的深度是递归的深度。

回溯法的模板如下

void backtracking(参数) {
     
    if (终止条件) {
     
        存放结果;#收集叶子节点
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
     
        处理节点;##如我们求数组【1234】的子集合，叶子节点有12，这里告诉12是如何来的。
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果##就是撤销处理节点 这一步。。。如求数组【1234】的组合，如开先放进了1，再放进了2，得到12为我们想要的组合。再把2回溯出去得到1，加入3，得到13组合
    }
}

回溯算法问题求解

1.组合问题

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

原始解法：for循环，k为2.两层for循环

n=4
results=[]
for i in range(1,n+1):
    for j  in range(i+1,n+1):
        result=str(i)+str(j)
        results.append(result)

print(results)

如果n为100，k为50呢，那就50层for循环，是不是开始窒息。

回溯算法求解
上面我们说了「要解决 n为100，k为50的情况，暴力写法需要嵌套50层for循环，那么回溯法就用递归来解决嵌套层数的问题」。
递归来做层叠嵌套（可以理解是开k层for循环），「每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了」。
此时递归的层数大家应该知道了，例如：n为100，k为50的情况下，就是递归50层。
一些同学本来对递归就懵，回溯法中递归还要嵌套for循环，可能就直接晕倒了！
如果脑洞模拟回溯搜索的过程，绝对可以让人窒息，所以需要抽象图形结构来进一步理解。
「我们在关于回溯算法，你该了解这些！中说道回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了」。
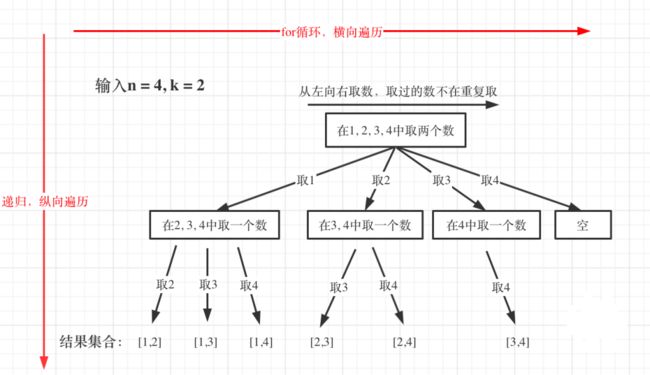
那么我把组合问题抽象为如下树形结构：

可以看出这个棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。
第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。
「每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围」。
「图中可以发现n相当于树的宽度，k相当于树的深度」。

那么如何在这个树上遍历，然后收集到我们要的结果集呢？

「图中每次搜索到了叶子节点，我们就找到了一个结果」。

相当于只需要把达到叶子节点的结果收集起来，就可以求得 n个数中k个数的组合集合。

解题步骤

第一步：这里要定义两个全局变量，一个用来存放符合条件单一结果path，一个用来存放符合条件结果的集合result。

第二步:函数里一定有两个参数，既然是集合n里面取k的数，那么n和k是两个int型的参数。
然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,…,n] ）。
为什么要有这个startIndex呢？
「每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex」。
从，在集合[1,2,3,4]取1之后，下一层递归，就要在[2,3,4]中取数了，那么下一层递归如何知道从[2,3,4]中取数呢，靠的就是startIndex。

终止条件
path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，

class Solution:
    def combine(self, n: int, k: int):
        result = []
        def recall(n, k, startindex, result, path):
            if len(path) == k:
                result.append(path[:])
                return
            for i in range(startindex, n+1):
                path.append(i)
                recall(n, k, i+1, result, path)
                path.pop()
        recall(n, k, 1, result, [])
        return result

c=Solution()
d=c.combine(n=4,k=2)
print(d)

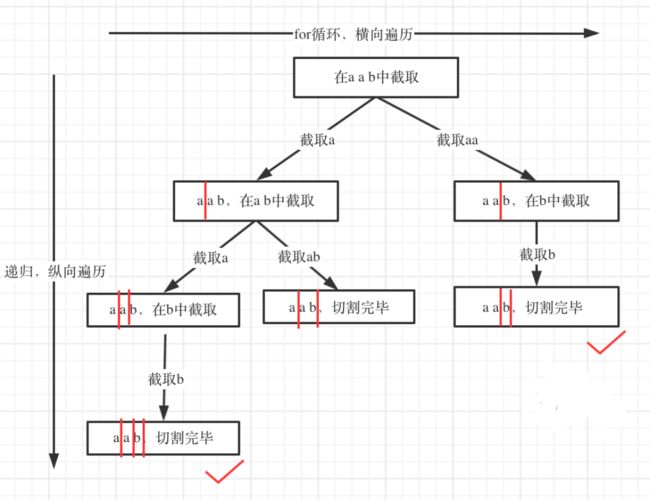
2.分割问题

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: “aab”
输出:
[
[“aa”,“b”],
[“a”,“a”,“b”]
]

class Solution:
    def partition(self, s: str):
        #判断是否回文
        def helper(subStr):
            i, j = 0, len(subStr) - 1
            while i <= j:
                if subStr[i] != subStr[j]:
                    return False
                i += 1
                j -= 1
            return True

        def recall(s, size, start, subset):
            if start == size:#如果遍历完啦，结束
                res.append(subset[:])
                return
            for i in range(start, size):
                if not helper(s[start:i + 1]):
                    continue
                subset.append(s[start:i + 1])#中见间结果
                #print(subset)
                recall(s, size, i + 1, subset)
                subset.pop()

        res = []
        size = len(s)
        recall(s, size, 0, [])
        return res




if __name__ == "__main__":
    s = "aab"
    split_result = Solution().partition(s)
    print(split_result)

3.子集问题

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        ans = []
        
        # 存储符合要求的子集
        tmp = []

        n = len(nums)
        def helper(idx):
            # 先添加子集
            ans.append(tmp[:])

            for i in range(idx, n):
                tmp.append(nums[i])
                # 避免重复，每次递归，从下一个索引开始
                helper(i+1)
                # 回溯
                tmp.pop()


        helper(0,0)
        return ans

4.全排列问题

给定一个 没有重复 数字的序列，返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

class Solution:
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        def backtrack(first = 0):
            # 所有数都填完了
            if first == n:  
                res.append(nums[:])
            for i in range(first, n):
                # 动态维护数组
                nums[first], nums[i] = nums[i], nums[first]
                # 继续递归填下一个数
                backtrack(first + 1)
                # 撤销操作
                nums[first], nums[i] = nums[i], nums[first]
        
        n = len(nums)
        res = []
        backtrack()
        return res