吴恩达机器学习——一元线性回归(1)
1.课程部分
1.1 基本概念
(1)训练集—由训练样例(training example)组成的集合就是训练集(training set),其中(x,y)是一个训练样例,(x(i),y(i))是第i个训练样例。
(2)假设函数—用学习算法对训练集数据训练,可以得到假设函数(Hypothesis Function),单变量线性回归的假设函数为: h θ ( x ) = θ 0 + θ 1 x h_θ (x)=θ_0+θ_1 x hθ(x)=θ0+θ1x, 为了方便 h θ ( x ) h_θ~(x) hθ (x)也可记作 h ( x ) h(x) h(x)。
(3)代价函数—指样本实际y值与预测标签之间的误差,表现形式很多,较常用的是平方的形式, J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ) 2 J(θ_0,θ_1)=\frac12m \sum_{i=1}^m(h_θ (x^{(i)} )-y^{(i)} ))^2 J(θ0,θ1)=21m∑i=1m(hθ(x(i))−y(i)))2。在实际算法中就是优化目标, 我们想要代价函数最小。
1.2 梯度下降
(1)梯度下降
梯度下降算法是一种优化算法,它可找到一个函数的局部极小值点。它的思想是, 首先随机选择 θ 0 , θ 1 θ_0,θ_1 θ0,θ1初始值,不断地改变它们的值使得 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)变小, 最终找到 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)的最小值点。(过程想象成下山坡,如想尽快的下坡,应每次都往坡度最大的方向下山。)
设置初始的,通过梯度下降算法迭代得出结果,迭代过程如下:

其中 α α α叫做学习率用来控制下降的幅度, α α α太小会使下降步长太短,收敛缓慢, α α α太大会造成震荡,无法结果收敛甚至发散。根据梯度选择合适的 α α α在实际应用中是有必要的。
如上图所示的情况,由于选择的初始值不同可能造成得到的结果不同,得到是局部最优的解。
(2)对于一元线性回归问题中的梯度下降算法
对于一元线性回归问题, J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)是一个凸函数,得到的解是全局最优。
其中,对 θ 0 , θ 1 θ_0,θ_1 θ0,θ1求导为:
∂ ( J ( θ 0 , θ 1 ) ) ∂ θ 0 = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{∂(J(θ_0,θ_1))}{∂θ_0} =\frac1m \sum_{i=1}^m (h_θ (x^{(i)})-y^{(i)} ) ∂θ0∂(J(θ0,θ1))=m1i=1∑m(hθ(x(i))−y(i))
∂ ( J ( θ 0 , θ 1 ) ) ∂ θ 1 = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) \frac{∂(J(θ_0,θ_1))}{∂θ_1} =\frac1m \sum_{i=1}^m (h_θ (x^{(i)})-y^{(i)} )x^{(i)} ∂θ1∂(J(θ0,θ1))=m1i=1∑m(hθ(x(i))−y(i))x(i)
2.习题
1.
答案: 4
2.
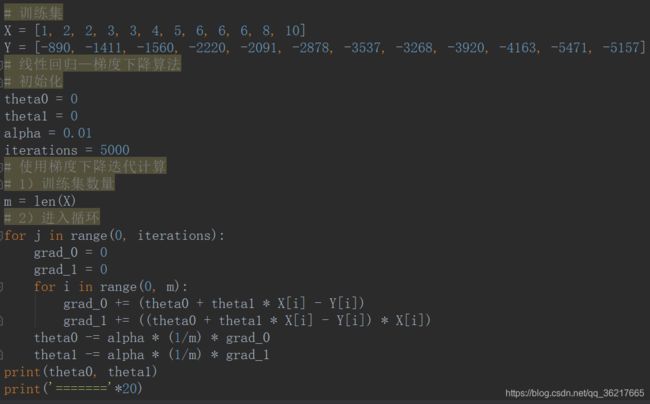
答案:θ0=−569.6, θ1=−530.9
代码实现:
3. Suppose we set θ0=−1, θ1=0.5. What is hθ(4)?
答案: 1
4.
答案:If the learning rate is too small, then gradient descent may take a very long time to converge.
5.
答案: Our training set can be fit perfectly by a straight line, i.e., all of our training examples lie perfectly on some straight line.