第五周【任务1】范数惩罚正则化 (笔记)

5.1 参数范数惩罚

正则化定义为"对学习算法的修改——旨在减少泛化误差而不是训练误差"。

• 参数惩罚：向机器学习模型添加限制参数值的额外约束

• 约束惩罚：向目标函数增加额外项来对参数值进行软约束

正则化的目标：降低过拟合，偏差换方差，提升泛化能力

注意:
我们其实永远不知道训练出来的模型是否包含数据生成过程(因为很难知道数据生成的物理规律，比如人 脸识别，目前还不知道人脑的机制)! 深度学习应用领域极为复杂，图像、语音、文本等，生成过程难以琢磨。事实上，最好的模型总是适当正则化的大型模型。

参数范数惩罚通常只惩罚权重$W$, 不管$b$：$b$是单变量，且容易过拟合。

对于修改的损失函数
$$\tilde{J}(\mathbf{\theta };\mathbf{X},\mathbf{y})=J(\mathbf{\theta };\mathbf{X},\mathbf{y})+\alpha \Omega (\mathbf{\theta })$$
$\alpha$是惩罚力度，$\Omega$是正则项

最常见的参数范数惩罚：

• $L_1$参数正则化
• $L_2$参数正则化

5.1.1 $L_2$参数正则化

$L_2$参数正则化（也称为岭回归，Tikhonov正则）通常被称为权重衰减(weight decay)，是通过向目标函数添加一个正则项$\Omega (\theta )=\frac{1}{2}\Vert \omega {\Vert }_2^2$使得权重更加接近原点。
$$\tilde{J}(\omega ;X,y)=J(\omega ;X,y)+\frac{\alpha }{2}{\omega }^T\omega$$
计算梯度
$${\nabla }_{\omega }\tilde{J}(\omega ;X,y)={\nabla }_{\omega }J(\omega ;X,y)+\alpha \omega$$
权重更新
$$\omega \leftarrow \omega -ϵ\left(\alpha \omega +{\nabla }_{\omega }J(\omega ;X,y)\right)=(1-ϵ\alpha )\omega -ϵ{\nabla }_{\omega }J(\omega ;X,y)$$
通过上式与无正则化的损失函数权重更新$\omega -ϵ{\nabla }_{\omega }J(\omega ;X,y)$对比，我们可以看出加入权重衰减后会导致学习规则的修改，也就是在每步执行梯度更新前先收缩权重（乘以$(1-\alpha ϵ)$），然后再减去梯度项。这样就相当于在更新权重的同时不断减小权重。

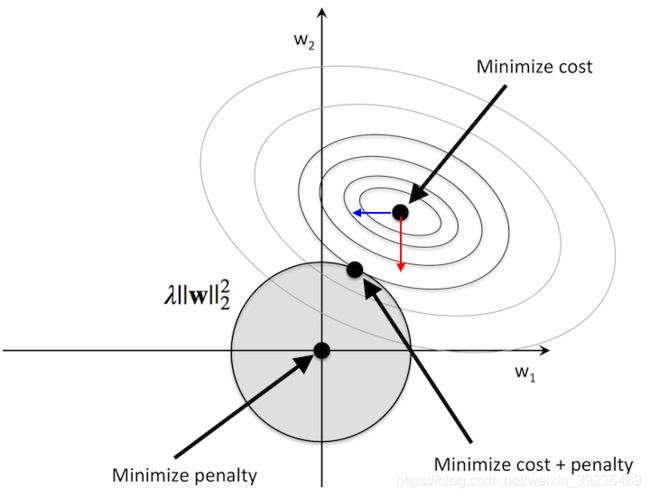
(图片来源：http://rasbt.github.io/mlxtend/user_guide/general_concepts/regularization-linear/)

图中的两类等高线分别代表没有正则化目标的等值线，以及$L_2$正则化项的等值线。在图中标出的交点，这两个竞争目标达到了平衡【因为我们同时在优化正则项和损失项，因此分别在向坐标原点和损失项极值点移动, 如果我们“固定”损失项的其中一根等值线（图中外向内第三根）而正则项圆的半径可以变化，那么正则项要最小化，必然就是取半径最小的、与前者相切的一根等值线，切点就是平衡点。另外一方面，在两个参数维度方向上，平衡点和损失项$J$极值点的变化率（梯度）不同。在$w_1$方向上，损失项$J$的梯度小，如果其极值点在向$w_1$轴原点移动（蓝箭头方向），损失项不会增加太多，但是却能有效减小正则项分量$w_1$；在$w_2$方向上，损失项$J$的梯度大，如果其极值点在向$w_2$轴原点移动（红箭头方向），虽然也能有效减小正则项分量$w_2$，但是损失项$J$就会增加很多。因此正则化项在优化过程中对$w_1$轴就有强烈影响偏好，倾向于将$w_1$拉向0，但是对$w_2$轴的偏好就会相对较小，$w_2$值衰减较慢。】。

总之，只有在显著减小目标函数方向上的参数会保留得相对完好。 在无助于目标函数减 小的方向上改变参数不会显著增加梯度。 这种不重要方向对应的分量会在训练过程中因正则化而衰减掉。

5.1.2 $L_1$参数正则化

定义
$$\Omega (\theta )=\Vert w{\Vert }_1=\sum _i\left|w_i\right|$$
目标函数
$$\tilde{J}(\omega ;X,y)=J(\omega ;X,y)+\alpha \Vert \omega {\Vert }_1$$
计算梯度
$${\nabla }_{\omega }\tilde{J}(\omega ;X,y)={\nabla }_{\omega }J(\omega ;X,y)+\alpha \mathrm{sgn}(\omega )$$
其中
$$\mathrm{sgn}(x):=\{\begin{array}{ll}-1& \text{ if }x<0\\ 0& \text{ if }x=0\\ 1& \text{ if }x>0\end{array}$$

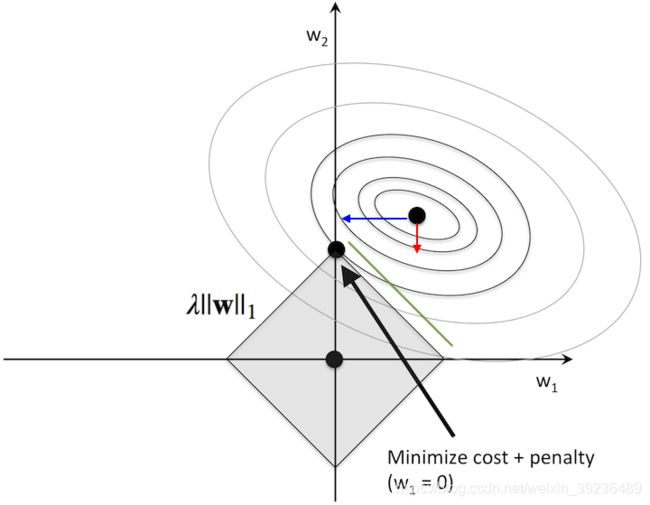
(图片来源：http://rasbt.github.io/mlxtend/user_guide/general_concepts/regularization-linear/)

【此时情况和$L_2$正则化相比就不太一样了。针对图中例子，损失项极值点在第一象限，且梯度曲面与上图相同，这就意味着$w_1$还是倾向于被减少。如果如果我们“固定”损失项的其中一根等值线（还是图中外向内第三根），由于等值线未必能够与斜率为-1的正则项边界相切，那么就导致平衡点更倾向于向边界与$w_2$轴的交点移动，一方面减少$w_1$的值，一方面“尽量“在等值线上且靠近坐标轴原点（对比绿线与损失项等值线的交点）】

因此对比可知，$L_1$正则化更容易导致参数稀疏。

5.2 作为约束的范数惩罚

考虑经过参数范数正则化的损失函数
$$\tilde{J}(\mathbf{\theta };\mathbf{X},\mathbf{y})=J(\mathbf{\theta };\mathbf{X},\mathbf{y})+\alpha \Omega (\mathbf{\theta })$$
之前我们在花书4.4节我们可以构造一个广义拉格朗日函数来最小化带约束函数，也就是在原始目标函数上添加一系列惩罚项。如果我们想约束$\Omega (\theta )$小于某个常数（就像上两张图那样），有
$$\{\begin{array}{l}\min J(\theta )\\ \Omega (\theta )\le k\end{array}$$

那么我们可以构建广义拉格朗日函数
$$\mathcal{L}(\mathbf{\theta },\alpha ;\mathbf{X},\mathbf{y})=J(\mathbf{\theta };\mathbf{X},\mathbf{y})+\alpha (\Omega (\mathbf{\theta })-k)$$
这个约束问题的解由下式给出
$${\theta }^{\ast }=\arg \underset{\mathbf{\theta }}{\min }\underset{\alpha ,\alpha \ge 0}{\max }\mathcal{L}(\mathbf{\theta },\alpha )=\underset{\alpha ,\alpha \ge 0}{\max }\underset{\theta }{\min }\mathcal{L}(\mathbf{\theta },\alpha )$$
其中
$$\underset{\theta }{\min }\mathcal{L}(\mathbf{\theta },\alpha )\iff J(\mathbf{\theta };\mathbf{X},\mathbf{y})+\alpha \Omega (\mathbf{\theta })$$
因此约束惩罚本质上与参数惩罚等价

5.3 正则化和欠约束问题

机器学习中许多线性模型，如求解线性回归和PCA，都依赖与矩阵$X^{T}X$求逆。
$$\begin{array}{l}\min J=\Vert xa-Y{\Vert }^2\\ \Rightarrow \frac{\partial J}{\partial a}=x^T(xa-Y)=0\\ \Rightarrow x^{T}xa=x^{T}Y\\ \Rightarrow a={\left(x^{T}x\right)}^{-1}{x}^{T}Y\end{array}$$
如果$X^{T}X$不可逆，这些方法就会失效。这种情况下，正则化的许多形式对应求逆$X^{T}X+\lambda I$，进而求解模型权重
$$\begin{array}{l}\min J=\Vert xa-Y{\Vert }^2+\lambda \Vert a{\Vert }^2\\ \Rightarrow \frac{\partial J}{\partial a}=x^{T}xa-x^{T}Y+\lambda a=0\\ \Rightarrow \left(x^{T}x+\lambda I\right)a=x^{T}Y\\ \Rightarrow a={\left(x^{T}x+\lambda I\right)}^{-1}{x}^{T}Y\end{array}$$
$X^{T}X+\lambda I$这个正则化矩阵是可逆的。大多数正则化方法能够保证应用于欠定问题的迭代方法收敛。

5.4 数据集增强

让机器学习模型泛化得更好的最好办法是使用更多的数据进行训练。 当然在实践中， 我们拥有的数据量是很有限的。 解决这个问题的一种方法是创建假数据并添加到训练集中。方式包括加入特定噪声(如高斯噪声)，做一定的几何变换等等。

• 数据集的各种变换，如对图像的平移、旋转和缩放。
• 在输入层注入噪声，也可以看作数据集增强的一种方法 (如去噪自编码器)。通过将随机噪声添加到输入再进 行训练能够大大改善神经网络的健壮性。

5.5 噪声鲁棒性

大多数数据集的y标签都有一定错误。 错误的y不利于最大化$\log p(y\mid x)$。 避免这种情况的一种方法是显式地对标签上的噪声进行建模。

例如，我们可以假设，对于一些小常数$ϵ$，训练集标记y是正确的概率是$1-ϵ$，(以$ϵ$的概率)任何其他可能的标签也可能是正确的。 这个假设很容易就能解析地与代价函数 结合，而不用显式地抽取噪声样本。

一个例子，假设一个样本的正确硬标签应该是$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$, 但是错误标记为$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$, 我们可以把标记改为软标签$\left[\begin{array}{c}0.05\\ 0.9\\ 0.05\end{array}\right]$，这样就算模型的预测输出的第二个输出维度是1，其他两个维度的标记也因为有微小值使得代价函数可以继续被学习，起到让模型向第一个维度输出1的方向学习的作用。

标签平滑： 通过把确切分类目标从0和1替换成$\frac{ϵ}{k-1}$和$1-ϵ$， 正则化具有k个输出的softmax函数的模型。

5.6 半监督学习

在半监督学习的框架下，$P(x)$产生的未标记样本和$P(x,y)$中的标记样本都用于估计$P(y|x)$或者根据x预测y。

在深度学习的背景下，半监督学习通常指的是学习一个表示(representation)$h=f(x)$。学习表示的目的是使相同类中的（未标注）样本有类似的表示。 无监督学习可以为如何在表示空间中聚集样本提供有用线索。 在输入空间紧密聚集的样本应该被映射到类似的表示。 在许多情况下，新空间上的线性分类器可以(根据这些学到的表示)达到较好的泛化。 这种方法的一个经典变种是使用主成分分析作为分类前(在投影后的数据上分类)的预处理步骤。

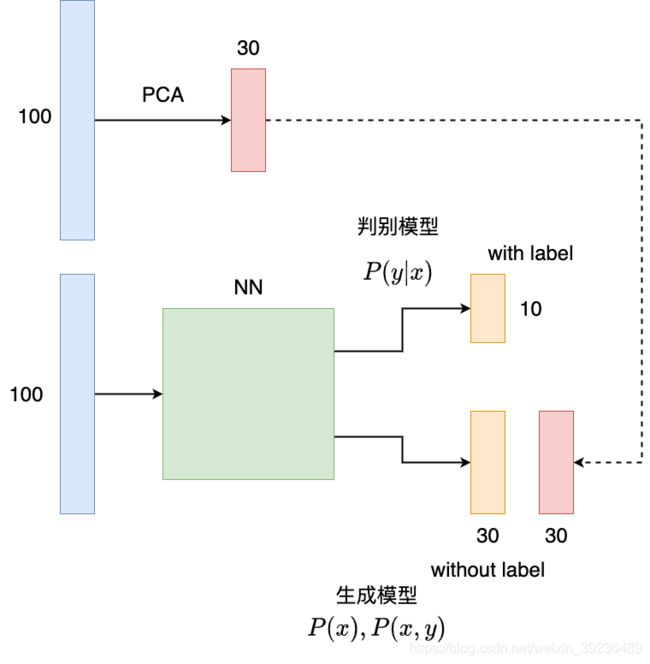
例如，我们假设有100个样本，其中50个有标记，剩下50个没有标记。每一个样本有100个特征维度，10个输出维度。那么我们可以首先通过PCA把50个未标记样本的维度从100降到30.然后我们把100个所有的样本一起放入一个神经网络进行训练。但是，输出上分成两条路径。一条路径是10维输出的分类器，另外一个路径是30维输出的无监督表示层。这样，有标签的样本就用标签来构建损失函数学习，无标签的样本就用PCA后的30维representation作为‘标签’来构建损失函数学习。两条路径共享一个神经网络进行训练学习。如下图

在这里, 有标签和无标签的分别是判别模型和生成模型。也就是说我们的神经网络不用分离无监督和监督部分，直接共享参数，在训练中权衡无监督（或生成）模型准则$-\log P(x)$ (或者$-\log P(x,y)$)和监督模型准则$-\log P(y\mid x)$。这里，生成模型准则表达了对监督学习问题解的特殊形式的先验知识，也就是说，$P(x)$的结构通过神经网络共享参数的方式连接到了$P(y\mid x)$. 通过训练中，控制生成模型准则，我们可以获得比纯粹生成模型，或者纯粹判别模型准则更好的权衡。

5.7 多任务学习

多任务学习是通过合并几个任务中的样例(可以视为对参数施加的软约束)来提高泛化的 一种方式。当模型的一部分被多个额外的任务共享时，这部分将被约束为良好的值， 通常会带来更好的泛化能力。

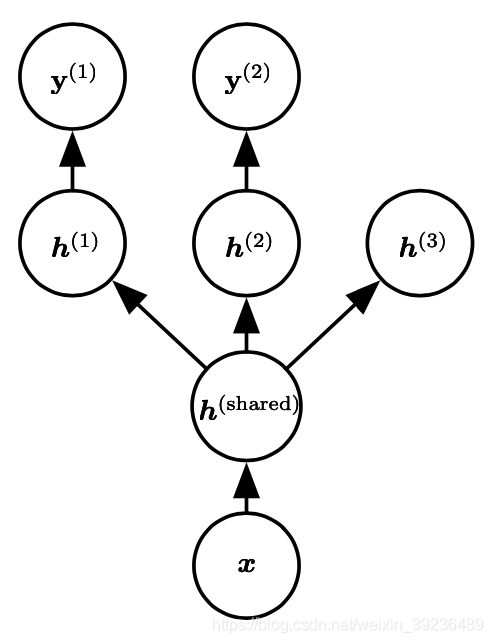
右图展示了多任务学习的一种普遍形式。不同的监督任务共享相同的输入 x 和中间表示层$h^{(shared)}$，能 学习共同的因素池。

(图片来源：花书page238)

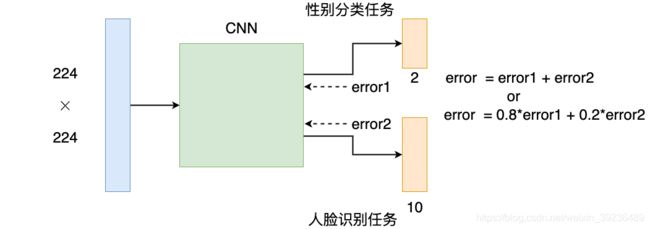
下面是一个人脸识别和性别分类的例子

输出的两个分类器维度分别是2和10，两个分类器的error可以先加和然后传回神经网络，也可以对不同任务有所偏重，对不同分类器的error先进行加权，然后相加。

5.8 提前终止

当训练有足够的表示能力甚至会过拟合的大模型时，我们经常观察到，训练误差会随着时间的推移逐渐降低但验证集的误差会再次上升。

这意味着我们只要返回使验证集误差最低的参数设置，就可以获得验证集误差更低的模型(并且因此有希望获得更好的测试误差)。 在每次验证集误差有所改善后，我们存储模型参数的副本。 当训练算法终止时，我们返回这些参数而不是最新的参数。 当验证集上的误差在事先指定的循环次数内没有进一步改善时，算法就会终止。

5.9 参数绑定和参数共享

有时我们需要对模型参数之间的相关型进行惩罚，使模型参数尽量接近或者相等。参数共享就是强迫模型某些参数相等，主要应用在卷积神经网络中。优点:显著降低了CNN模型的参数数量(CNN模型参数数量经常是千万量级以上)， 减少模型所占用的内存，并且显著提高了网络大小而不需要相应的增加训练数据。

参数共享有两种。

5.9.1 层内共享

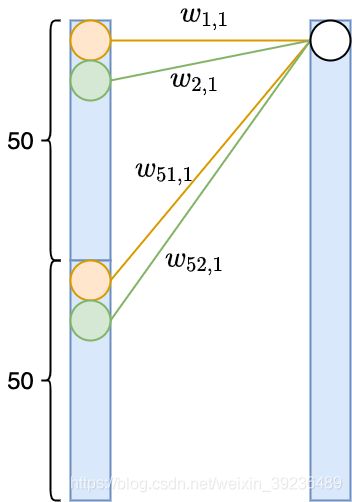
假设我们有两个相邻的网络层，维度都是100.对左边第1个和第51个神经元与右边第一个神经元链接的神经，我们可以强迫他们相等$w_{1,1}=w_{51,1}$。类似，对左边第1个和第51个神经元与右边第一个神经元链接的神经，我们可以强迫他们相等$w_{2,1}=w_{52,1}$。这样，左边网络层其实就是上下两个相同的50维网络层拼接在一起，这样就减少了一半的参数数量。

5.9.2 层间共享

我们也可以在强迫两个不同层间的参数矩阵$W_1$和$W_2$的部分参数相等，甚至极端一点,干脆让$W_1=W_2$。

5.10 稀疏表示

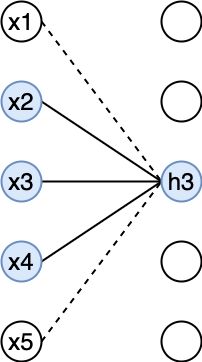
稀疏表示是惩罚神经网络的激活单元，稀疏化激活单元。换言之， 稀疏表示是使得每个神经元的输入单元变得稀疏，很多输入是0

例如上图，$h_3$只依赖于上一层的3个神经元输 入$x_2,x_3,x_4$ ，而其他神经元到 $h_3$ 的输入 都是0。

5.11 Bagging和其他集成方法

Bagging(bootstrap aggregating)是通过结合几个模型降低泛化误差的技术。主要想法是分别训练几个不同的模型，然后让所有模型表决测试样例的输出。这是机器学习 中常规策略的一个例子,被称为模型平均(model averaging)。采用这种策略的技术被称为集成方法。

Bagging是一种允许重复多次使用同一种模型、训练算法和目标函数的方法。具体来说,Bagging涉及构造 k 个不同的数据集。每个数据集从原始数据集中重复采样构成， 和原始数据集具有相同数量的样例。

假设我们有k个回归模型，每个模型的误差是${ϵ}_i$，误差服从0均值、方差是$v$、协方差是$c$的多维正态分布。那么模型的平均预测误差是
$$\begin{gathered} \mathbb{E}\left[{\left(\frac{1}{k}\sum _i{ϵ}_i\right)}^2\right]=\frac{1}{k^2}\mathbb{E}\left[\sum _i{ϵ}_i^2+\sum _{i\ne j}{ϵ}_i{ϵ}_j\right] \\ =\frac{1}{k^2}\mathbb{E}\left[kv+k(k-1)c\right]=\frac{1}{k}v+\frac{k-1}{k}c \end{gathered}$$
如果误差完全相关，$c=v$， 均方误差就是$v$， 模型平均对提高预测没有帮助。如果误差完全不相关$c=0$，模型平均的均方误差的期望就是$\frac{v}{k}$。这就说明集成均方误差的期望随集成规模的增大而线性减少

【$({ϵ}_i+{ϵ}_j{)}^2={ϵ}_i^2+{ϵ}_j^2+{ϵ}_i{ϵ}_j+{ϵ}_j{ϵ}_i$】

5.12 Dropout

Dropout可以被认为是集成大量深层神经网络的实用Bagging方法。但是Bagging方法涉及训练多个模型，并且在每个测试样本上评估多个模型。当每个模型都是一个大型神经网络时，Bagging方法会耗费很多的时间和内存。而Dropout则提供了一种廉价的 Bagging集成近似，能够训练和评估指数级数量的神经网络。

在神经网络中，dropout可以起到正则化的作用:

i. Dropout is a form of model averaging. In particular, for a layer of H nodes, we sampling from 2H architectures, where we choose an arbitrary subset of the nodes to remain active. The weights learned are shared across all these models means that the various models are regularizing the other models.

ii. Dropout helps prevent feature co-adaptation, which has a regularizing effect.

iii. Dropout adds noise to the learning process, and training with noise in general has a regularizing effect.

iv. Dropout leads to more sparsity in the hidden units, which has a regularizing effect. (Note that in one of the lecture videos, this was phrased as dropout “shrinking the weights” or “spreading out the weights”. We will also accept this phrasing.)

效果: Dropout比其他标准正则化方法更有效， 同时可以跟其他形式正则一起使用

优点：计算量小，不限制模型和训练过程