机器学习入门实践——线性回归模型(波士顿房价预测)
机器学习入门实践——线性回归模型(波士顿房价预测)
一、背景介绍
给定一个大小为 n n n的数据集 { y i , x i 1 , . . . , x i d } i = 1 n {\{y_{i}, x_{i1}, ..., x_{id}\}}_{i=1}^{n} { yi,xi1,...,xid}i=1n,其中 x i 1 , … , x i d x_{i1}, \ldots, x_{id} xi1,…,xid是第 i i i个样本 d d d个属性上的取值, y i y_i yi是该样本待预测的目标。线性回归模型假设目标 y i y_i yi可以被属性间的线性组合描述,即
y i = ω 1 x i 1 + ω 2 x i 2 + … + ω d x i d + b , i = 1 , … , n y_i = \omega_1x_{i1} + \omega_2x_{i2} + \ldots + \omega_dx_{id} + b, i=1,\ldots,n yi=ω1xi1+ω2xi2+…+ωdxid+b,i=1,…,n
例如,在我们将要建模的房价预测问题里, x i j x_{ij} xij是描述房子 i i i的各种属性(比如房间的个数、周围学校和医院的个数、交通状况等),而 y i y_i yi是房屋的价格。
二、效果展示
我们使用从UCI Housing Data Set获得的波士顿房价数据集进行模型的训练和预测。下面的散点图展示了使用模型对部分房屋价格进行的预测。其中,每个点的横坐标表示同一类房屋真实价格的中位数,纵坐标表示线性回归模型根据特征预测的结果,当二者值完全相等的时候就会落在虚线上。所以模型预测得越准确,则点离虚线越近。
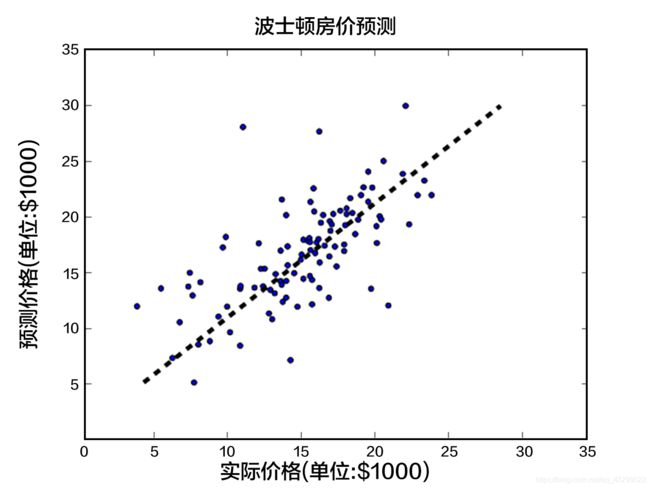
图1. 预测值 V.S. 真实值
三、模型假设
在波士顿房价数据集中,和房屋相关的值共有14个:前13个用来描述房屋相关的各种信息,即模型中的 x i x_i xi;最后一个值为我们要预测的该类房屋价格的中位数,即模型中的 y i y_i yi。因此,我们的模型就可以表示成:
Y ^ = ω 1 X 1 + ω 2 X 2 + … + ω 13 X 13 + b \hat{Y} = \omega_1X_{1} + \omega_2X_{2} + \ldots + \omega_{13}X_{13} + b Y^=ω1X1+ω2X2+…+ω13X13+b
Y ^ \hat{Y} Y^ 表示模型的预测结果,用来和真实值 Y Y Y区分。模型要学习的参数即: ω 1 , … , ω 13 , b \omega_1, \ldots, \omega_{13}, b ω1,…,ω13,b。
建立模型后,我们需要给模型一个优化目标,使得学到的参数能够让预测值 Y ^ \hat{Y} Y^尽可能地接近真实值 Y Y Y。这里我们引入损失函数(Loss Function,或Cost Function)这个概念。 输入任意一个数据样本的目标值 y i y_{i} yi和模型给出的预测值 y i ^ \hat{y_{i}} yi^,损失函数输出一个非负的实值。这个实值通常用来反映模型误差的大小。
对于线性回归模型来讲,最常见的损失函数就是均方误差(Mean Squared Error, MSE)了,它的形式是:
M S E = 1 n ∑ i = 1 n ( Y i ^ − Y i ) 2 MSE=\frac{1}{n}\sum_{i=1}^{n}{(\hat{Y_i}-Y_i)}^2 MSE=n1i=1∑n(Yi^−Yi)2
即对于一个大小为 n n n的测试集, M S E MSE MSE是 n n n个数据预测结果误差平方的均值。
对损失函数进行优化所采用的方法一般为梯度下降法。梯度下降法是一种一阶最优化算法。如果 f ( x ) f(x) f(x)在点 x n x_n xn有定义且可微,则认为 f ( x ) f(x) f(x)在点 x n x_n xn沿着梯度的负方向 − ▽ f ( x n ) -▽f(x_n) −▽f(xn)下降的是最快的。反复调节 x x x,使得 f ( x ) f(x) f(x)接近最小值或者极小值,调节的方式为:
x n + 1 = x n − λ ▽ f ( x ) , n ≧ 0 x_n+1=x_n-λ▽f(x), n≧0 xn+1=xn−λ▽f(x),n≧0
其中λ代表学习率。这种调节的方法称为梯度下降法。
四、导入模块
首先我们引入必要的库:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# Window系统下设置字体为SimHei
plt.rcParams['font.sans-serif'] = ['SimHei']
# Mac系统下设置字体为Arial Unicode MS
# plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
%matplotlib inline
五、载入数据
from sklearn import datasets
# 加载波士顿房价的数据集
boston = datasets.load_boston()
1、打印数据
print(boston)
# 先要查看数据的类型,是否有空值,数据的描述信息等等。
boston_df = pd.DataFrame(boston.data, columns=boston.feature_names)
boston_df['PRICE'] = boston.target
# 查看数据是否存在空值,从结果来看数据不存在空值。
boston_df.isnull().sum()
# 查看数据大小
boston_df.shape
# 显示数据前5行
boston_df.head()
2、数据集介绍
这份数据集共506行,每行包含了波士顿郊区的一类房屋的相关信息及该类房屋价格的中位数。其各维属性的意义如下:
| 属性名 | 解释 | 类型 |
|---|---|---|
| CRIM | 该镇的人均犯罪率 | 连续值 |
| ZN | 占地面积超过25,000平方呎的住宅用地比例 | 连续值 |
| INDUS | 非零售商业用地比例 | 连续值 |
| CHAS | 是否邻近 Charles River(查尔斯河) | 离散值,1=邻近;0=不邻近 |
| NOX | 一氧化氮浓度 | 连续值 |
| RM | 每栋房屋的平均客房数 | 连续值 |
| AGE | 1940年之前建成的自用单位比例 | 连续值 |
| DIS | 到波士顿5个就业中心的加权距离 | 连续值 |
| RAD | 到径向公路的可达性指数 | 连续值 |
| TAX | 全值财产税率 | 连续值 |
| PTRATIO | 学生与教师的比例 | 连续值 |
| B | 1000(BK - 0.63)^2,其中BK为黑人占比 | 连续值 |
| LSTAT | 低收入人群占比 | 连续值 |
| MEDV | 同类房屋价格的中位数 | 连续值 |
3、连续值与离散值
观察一下数据,我们的第一个发现是:所有的13维属性中,有12维的连续值和1维的离散值(CHAS)。离散值虽然也常使用类似0、1、2这样的数字表示,但是其含义与连续值是不同的,因为这里的差值没有实际意义。例如,我们用0、1、2来分别表示红色、绿色和蓝色的话,我们并不能因此说“蓝色和红色”比“绿色和红色”的距离更远。所以通常对一个有 d d d个可能取值的离散属性,我们会将它们转为 d d d个取值为0或1的二值属性或者将每个可能取值映射为一个多维向量。不过就这里而言,因为CHAS本身就是一个二值属性,就省去了这个麻烦。
# 查看数据的描述信息,在描述信息里可以看到每个特征的均值,最大值,最小值等信息。
boston_df.describe()
# 清洗'PRICE' = 50.0 的数据
boston_df = boston_df.loc[boston_df['PRICE'] != 50.0]
六、数据可视化
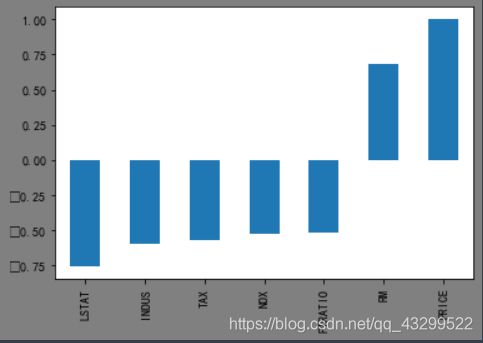
1、将每一个特征和房价的相关系数大于0.5的特征画图显示出来
# 计算每一个特征和房价的相关系数
boston_df.corr()['PRICE']
# 可以看出LSTAT、PTRATIO、RM三个特征的相关系数大于0.5,这三个特征和价格都有明显的线性关系。
plt.figure(facecolor='gray')
corr = boston_df.corr()
corr = corr['PRICE']
corr[abs(corr) > 0.5].sort_values().plot.bar()
2、分别画出房价关于LSTAT、PTRATIO、RM三个特征的散点图
# LSTAT 和房价的散点图
plt.figure(facecolor='gray')
plt.scatter(boston_df['LSTAT'], boston_df['PRICE'], s=30, edgecolor='white')
plt.title('LSTAT')
plt.show()
# PTRATIO 和房价的散点图
plt.figure(facecolor='gray')
plt.scatter(boston_df['PTRATIO'], boston_df['PRICE'], s=30, edgecolor='white')
plt.title('PTRATIO')
plt.show()
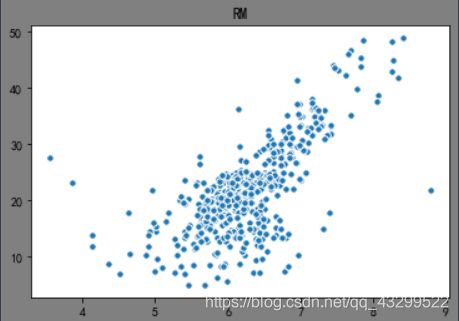
# RM 和房价的散点图
plt.figure(facecolor='gray')
plt.scatter(boston_df['RM'], boston_df['PRICE'], s=30, edgecolor='white')
plt.title('RM')
plt.show()
七、数据预处理
1、异常数据处理
根据散点图分析,房屋的’RM’, ‘LSTAT’,'PTRATIO’特征与房价的相关性最大,所以,将其余不相关特征移除。
boston_df = boston_df[['LSTAT', 'PTRATIO', 'RM', 'PRICE']]
# 目标值
y = np.array(boston_df['PRICE'])
boston_df = boston_df.drop(['PRICE'], axis=1)
# 特征值
X = np.array(boston_df)
2、划分训练集与测试集
我们将数据集分割为两份:一份用于调整模型的参数,即进行模型的训练,模型在这份数据集上的误差被称为训练误差;另外一份被用来测试,模型在这份数据集上的误差被称为测试误差。我们训练模型的目的是为了通过从训练数据中找到规律来预测未知的新数据,所以测试误差是更能反映模型表现的指标。分割数据的比例要考虑到两个因素:更多的训练数据会降低参数估计的方差,从而得到更可信的模型;而更多的测试数据会降低测试误差的方差,从而得到更可信的测试误差。我们这个例子中设置的分割比例为 8 : 2 8:2 8:2
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=0.2,
random_state=0)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
3、数据归一化
由于各维属性的取值范围差别很大(如图2所示)。例如,属性B的取值范围是[0.32, 396.90],而属性NOX的取值范围是[0.3850, 0.8170]。这里就要用到一个常见的操作-归一化。归一化的目标是把各位属性的取值范围放缩到差不多的区间,例如[-0.5,0.5]。这里我们使用一种很常见的操作方法:减掉均值,然后除以原取值范围。
做归一化至少有以下3个理由:
-
过大或过小的数值范围会导致计算时的浮点上溢或下溢。
-
不同的数值范围会导致不同属性对模型的重要性不同,而这个隐含的假设常常是不合理的。这会对优化的过程造成困难,使训练时间大大的加长。
-
很多的机器学习技巧/模型(例如L1,L2正则项,向量空间模型-Vector Space Model)都基于这样的假设:所有的属性取值都差不多是以0为均值且取值范围相近的。

图2. 各维属性的取值范围
from sklearn import preprocessing
# 初始化标准化器
min_max_scaler = preprocessing.MinMaxScaler()
# 分别对训练和测试数据的特征以及目标值进行标准化处理
X_train = min_max_scaler.fit_transform(X_train)
y_train = min_max_scaler.fit_transform(y_train.reshape(-1,1)) # reshape(-1,1)指将它转化为1列,行自动确定
X_test = min_max_scaler.fit_transform(X_test)
y_test = min_max_scaler.fit_transform(y_test.reshape(-1,1))
八、模型训练
采用线性回归模型LinearRegression进行训练及预测
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 使用训练数据进行参数估计
lr.fit(X_train, y_train)
# 使用测试数据进行回归预测
y_test_pred = lr.predict(X_test)
九、模型评估
r2_score()函数可以表示特征模型对特征样本预测的好坏,即确定系数。
# 使用r2_score对模型评估
from sklearn.metrics import mean_squared_error, r2_score
# 绘图函数
def figure(title, *datalist):
plt.figure(facecolor='gray', figsize=[16, 8])
for v in datalist:
plt.plot(v[0], '-', label=v[1], linewidth=2)
plt.plot(v[0], 'o')
plt.grid()
plt.title(title, fontsize=20)
plt.legend(fontsize=16)
plt.show()
# 训练数据的预测值
y_train_pred = lr.predict(X_train)
# 计算均方差
train_error = [mean_squared_error(y_train, [np.mean(y_train)] * len(y_train)),
mean_squared_error(y_train, y_train_pred)]
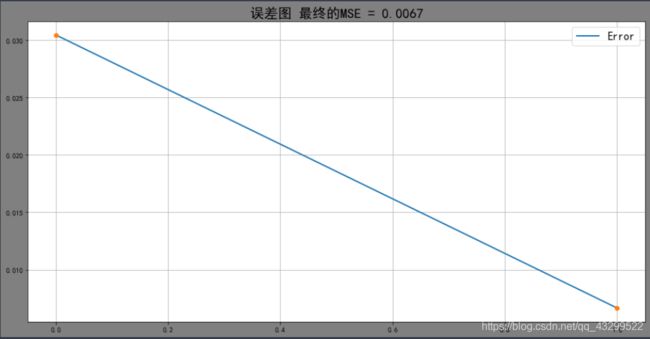
# 绘制误差图
figure('误差图 最终的MSE = %.4f' % (train_error[-1]), [train_error, 'Error'])
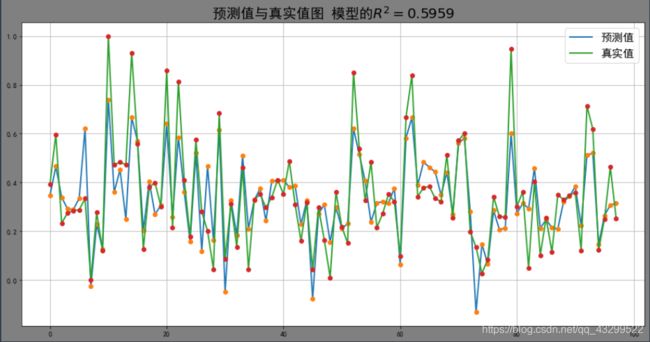
# 绘制预测值与真实值图
figure('预测值与真实值图 模型的' + r'$R^2=%.4f$' % (r2_score(y_train_pred, y_train)), [y_test_pred, '预测值'],
[y_test, '真实值'])
# 绘制预测值与真实值图
figure('预测值与真实值图 模型的' + r'$R^2=%.4f$' % (r2_score(y_train_pred, y_train)), [y_test_pred, '预测值'],
[y_test, '真实值'])
根据预测值和真实值的对比图,其中线性回归模型的决定系数为0.5959,说明线性关系可以解释房价的59.59%。
# 线性回归的系数
print('线性回归的系数为:\n w = %s \n b = %s' % (lr.coef_, lr.intercept_))
十、总结
我们借助波士顿房价这一数据集,介绍了线性回归模型的基本概念,以及如何使用Sklearn提供的线性回归模型实现训练和测试的过程。很多的模型和技巧都是从简单的线性回归模型演化而来,因此弄清楚线性回归模型的原理和局限非常重要。