AFA人工鱼群算法函数优化求解实例C++(2020.11.4)
AF人工鱼群算法C++
- 人工鱼群算法Artificial Fish
-
- 1 基本思想
- 2 算法介绍
-
- 2.1 一些定义
- 2.2 行为描述
-
- 2.2.1 觅食行为
- 2.2.2 聚群行为
- 2.2.3 追尾行为
- 2.2.4 随机行为
- 2.3 行为选择
- 2.4 公告板
- 2.5 终止条件
- 3 算法步骤
- 4 函数优化实例
-
- 4.1 目标函数
- 4.2 C++源代码(AFA)
- 4.3 运行结果
- 5 算法特点
人工鱼群算法Artificial Fish
1 基本思想
鱼群算法的基本思想是设想一片水域,如果某个地方的鱼类数目最多,那么这个地方一般来说就是水域内富含营养物质最多的地方,依据这一特点来模仿鱼群的觅食等行为,以实现全局寻优的目的。
鱼群模式中,鱼类的活动主要分为四种:觅食行为、聚群行为、追尾行为和随机行为。
2 算法介绍
这样,在类中将人工鱼的自身信息和一些行为进行封装,并且它的状态可以被同伴感知到。
2.1 一些定义
向量 X = ( x 1 , x 2 , . . . , x n ) X=(x_1,x_2,...,x_n) X=(x1,x2,...,xn) 表示人工鱼个体的状态,其中 x i ( i = 1 , 2 , . . . , n ) x_i(i=1,2,...,n) xi(i=1,2,...,n)为欲寻优的变量;
Y = f ( X ) Y=f(X) Y=f(X) 表示人工鱼当前所在位置的食物浓度,其中 Y Y Y为目标函数值;
d i , j = ∣ ∣ X i − X j ∣ ∣ d_{i,j}=||X_i -X_j|| di,j=∣∣Xi−Xj∣∣ 表示人工鱼个体之间的距离;
V i s u a l Visual Visual 表示人工鱼的感知距离;
s t e p step step 表示人工鱼移动的最大步长; δ δ δ为拥挤度因子。
2.2 行为描述
人工鱼(artificial fish,AF)的主要行为如下:
2.2.1 觅食行为
觅食行为指鱼循着事物多的方向游动的一种行为,人工鱼 X i X_i Xi在其视野内随机选择一个状态 X j X_j Xj,分别计算它们的目标函数值进行比较,如果发现 Y j Y_j Yj比 Y i Y_i Yi优,则 X i X_i Xi向 X j X_j Xj的方向移动一步;否则, X i X_i Xi继续在其视野内随机选择状态 X j X_j Xj,判断是否满足前进条件;这样反复尝试 t r y − n u m b e r try_{-}number try−number次后,如果仍不满足前进条件,则随机移动一步。
伪代码描述如下:
f l o a t A r t i f i c i a l − f i s h : : A F − p r e y ( ) float Artificial_{-}fish::AF_{-}prey() floatArtificial−fish::AF−prey()
{
f o r ( i = 0 ; i < t r y − n u m b e r ; i + + ) for(i=0;i
{
X j = X i + R a n d ( ) ⋅ V i s u a l ; X_j = X_i+Rand()\cdot Visual; Xj=Xi+Rand()⋅Visual;
i f ( Y i < Y j ) if (Y_i
X i ∣ n e x t = X i + R a n d ( ) ⋅ S t e p ⋅ X j − X i ∣ ∣ X j − X i ∣ ∣ ; X_{i|next}=X_i+Rand()\cdot Step \cdot \frac {X_j -X_i}{||X_j-X_i||}; Xi∣next=Xi+Rand()⋅Step⋅∣∣Xj−Xi∣∣Xj−Xi;
e l s e else else
X i ∣ n e x t = X i + R a n d ( ) ⋅ S t e p X_{i|next}=X_i+Rand()\cdot Step Xi∣next=Xi+Rand()⋅Step
}
r e t u r n A F − f o o d c o n s i s t e n c e ( X i ∣ n e x t ) return AF_{-}foodconsistence(X_{i|next}) returnAF−foodconsistence(Xi∣next)
}
2.2.2 聚群行为
鱼在游动过程中为了保证自身的生存和躲避危害会自然地聚集成群。鱼群聚集时所遵守的规则有三条:①分割规则,尽量避免与邻近伙伴过于拥挤; ②对准规则,尽量与邻接伙伴的平均方向一致; ③内聚规则,尽量朝邻近伙伴的重心移动。人工鱼 X i X_i Xi搜索其视野内(即 d i , j < V i s u a l d_{i,j}
伪代码描述如下:
f l o a t A r t i f i c i a l − f i s h : : A F − s w a r m ( ) float Artificial_{-}fish::AF_{-}swarm() floatArtificial−fish::AF−swarm()
{
n f = 0 ; X C = 0 ; n_f=0;X_C=0; nf=0;XC=0;
f o r ( j = 0 ; j < f r i e n d − n u m b e r ; j + + ) for(j=0;j
i f ( d i , j < V i s u a l ) if (d_{i,j}
X C = X C n f ; X_C = \frac{X_C}{n_f}; XC=nfXC;
i f ( Y C n f > δ Y i ) if(\frac{Y_C}{n_f} >δY_i) if(nfYC>δYi)
X i ∣ n e x t = X i + R a n d ( ) ⋅ S t e p ⋅ X C − X i ∣ ∣ X C − X i ∣ ∣ ; X_{i|next}=X_i+Rand()\cdot Step \cdot \frac {X_C -X_i}{||X_C-X_i||}; Xi∣next=Xi+Rand()⋅Step⋅∣∣XC−Xi∣∣XC−Xi;
e l s e else else
A F − p r e y ( ) ; AF_{-}prey(); AF−prey();
r e t u r n A F − f o o d c o n s i s t e n c e ( X i ∣ n e x t ) return AF_{-}foodconsistence(X_{i|next}) returnAF−foodconsistence(Xi∣next)
}
2.2.3 追尾行为
鱼向其可视区域内的最优方向移动的一种行为。人工鱼 X i X_i Xi搜索其视野内所有伙伴中的函数最优伙伴 X j X_j Xj。如果 Y C / n f > δ Y i Y_C/n_f >δY_i YC/nf>δYi,表明最优伙伴 X j X_j Xj具有较高的食物浓度并且其周围不太拥挤,则 X i X_i Xi朝伙伴 X j X_j Xj的方向前进异步;否则执行觅食行为。
伪代码描述如下:
f l o a t A r t i f i c i a l − f i s h : : A F − f o l l o w ( ) float Artificial_{-}fish::AF_{-}follow() floatArtificial−fish::AF−follow()
{
Y m a x = − ∞ ; Y_max =- \infty; Ymax=−∞;
f o r ( j = 0 ; j < f r i e n d − n u m b e r ; j + + ) for(j=0;j
i f ( d i , j < V i s u a l if(d_{i,j}
Y m a x = Y j ; X m a x = X j ; {Y_{max}=Y_j;X_{max}=X_j;} Ymax=Yj;Xmax=Xj;
n f = 0 ; n_f=0; nf=0;
f o r ( j = 0 ; j < f r i e n d − n u m b e r ; j + + ) for(j=0;j
i f ( d m a x , j < V i s u a l ) if(d_{max,j}
i f ( Y m a x n f > δ Y i ) if(\frac{Y_max}{n_f}>δY_i) if(nfYmax>δYi)
X i ∣ n e x t = X i + R a n d ( ) ⋅ S t e p ⋅ X m a x − X i ∣ ∣ X m a x − X i ∣ ∣ X_{i|next}=X_i+Rand()\cdot Step\cdot \frac{X_{max}-X_i}{||X_{max}-X_i||} Xi∣next=Xi+Rand()⋅Step⋅∣∣Xmax−Xi∣∣Xmax−Xi
e l s e else else
A F − p r e y ( ) ; AF_{-}prey(); AF−prey();
r e t u r n A F − f o o d c o n s i s t e n c e ( X i ∣ n e x t ) ; return AF_{-}foodconsistence(X_{i|next}); returnAF−foodconsistence(Xi∣next);
}
2.2.4 随机行为
随机行为指人工鱼在视野内随机移动,当发现食物时,会向食物逐渐增多的方向快速移动。随机行为的实现较为简单,就是向视野中随机选择一个状态的方向移动,本质上讲它是觅食行为的一个缺省行为。
2.3 行为选择
根据所要解决的问题性质,需要对人工鱼当前环境进行评价后来选择一种行为。而较常用的评价方法及时选择各行为中使得向最优方向前进最大的行为,也就是个性为中使得人工鱼的下一个状态最优的行为,如果没有能使下一状态优于当前状态的行为,则采取随机行为。
2.4 公告板
公告板是记录最优人工鱼个体状态的地方。每条人工鱼在执行完一次迭代后将自身当前状态与公告板中记录的状态进行比较,若优于公告板中的状态则用自身状态更新,否则公告板的状态不变。当整个算法的迭代结束后,输出公告板的值,就是所求的最优值。
2.5 终止条件
①判断连续多次所得的均方差小于允许的误差;
②判断一些区域的人工鱼群的数量达到某个比率;
③连续多次所获取的值均不得超过以寻找的极值;
④迭代次数到达设定的最大次数。
3 算法步骤
步骤1:初始化,确定种群规模N,在变量可行域内随机生成 N N N个个体,设定人工鱼的可视域 V i s u a l Visual Visual,步长 s t e p step step,拥挤度因子 δ δ δ,尝试次数 t r y − n u m b e r try_{-}number try−number;
步骤2:计算初始鱼群各个体的适应值,取最优人工鱼状态及其值赋给公告板;
步骤3:个体通过觅食行为、聚群行为、追尾行为更新自己,生成新鱼群;
步骤4:评价所有个体,若某个体优于公告板,则将公告板更新为该个体;
步骤5:当公告板上最优解达到满意误差界内,算法结束;否则转到步骤3.
4 函数优化实例
4.1 目标函数
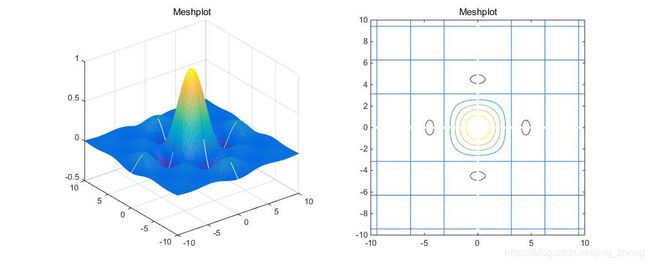
f ( x , y ) = s i n ( x ) x s i n ( y ) y f(x,y) = \frac{sin(x)}{x} \frac{sin(y)}{y} f(x,y)=xsin(x)ysin(y)
其中, $s.t. $ x ∈ [ − 10 , 10 ] x∈[-10,10] x∈[−10,10] y ∈ [ − 10 , 10 ] y∈[-10,10] y∈[−10,10]
Matlab绘制函数图像代码如下:
X=-10:0.1:10;
Y=-10:0.1:10;
[XX,YY]=meshgrid(X,Y);
Z=sin(XX).*sin(YY)./(XX.*YY);
figure
subplot(1,2,1)
mesh(XX,YY,Z);title('Meshplot');
subplot(1,2,2)
contour(XX,YY,Z);title('Meshplot');
函数图像如上图所示,该函数的极点位于 ( 0 , 0 ) (0,0) (0,0)处,极值为1,可以看出,该非线性函数在全局极大值的周围密布着许多局部极值,通常的寻优算法极易陷入局部极值在各局部极值间振荡,比较适用于验证算法的性能。
4.2 C++源代码(AFA)
main.cpp
#include fitfunctionvalue() > bestfitvalue)
{
for (int j = 0; j < Dimension; j++)
Bestfish.X[j] = (af + i)->X[j];
}*/
}
double Distance(AF af1, AF af2)//计算两条鱼距离的函数
{
double dist = 0;
for (int i = 0; i < Dimension; i++)
dist += pow(af1.X[i] - af2.X[i], 2.0);
dist = sqrt(dist / float(Dimension));
return dist;
}
void prey(int id)//觅食行为
{
AF AFNew;
AFNew.Init(Dimension);
for (int i = 0; i < try_number; i++)
{
for (int j = 0; j < Dimension; j++)
AFNew.X[j] = (af+id)->X[j] + r(random) * visual;
double Yi = 0, Yj = 0;
Yi = (af + id)->fitfunctionvalue();
Yj = AFNew.fitfunctionvalue();
if (Yi < Yj)
{
for (int j = 0; j < Dimension; j++)
(af + id)->X[j] = (af + id)->X[j] + r(random)*step*(AFNew.X[j] - (af + id)->X[j]) / Distance(AFNew, *(af+id));
}
else
{
for (int j = 0; j < Dimension; j++)
(af + id)->X[j] = (af + id)->X[j] + r(random)*step;
}
}
}
void swarm(int id)//聚群行为
{
AF AFXc;
AFXc.Init(Dimension);
for (int j = 0; j < Dimension; j++) AFXc.X[j] = 0;
double nf = 0;
for (int i = 0; i < N; i++)
if ((Distance(*(af + id), *(af + i)) < visual) && (Distance(*(af+id), *(af + i)) != 0))
{
nf++;
for (int j = 0; j < Dimension; j++)
AFXc.X[j] += (af + i)->X[j];
}
for (int j = 0; j < Dimension; j++)
AFXc.X[j] = AFXc.X[j] / nf;//计算邻域伙伴的中心位置
double Yc= AFXc.fitfunctionvalue(), Yi=(af+id)->fitfunctionvalue();
if (Yc / nf > delta*Yi)
{
for (int j = 0; j < Dimension; j++)
(af + id)->X[j] = (af + id)->X[j] + r(random)*step*(AFXc.X[j] - (af + id)->X[j]) / Distance(AFXc, *(af + id));
}
else
prey(id);
}
void follow(int id)//追尾行为
{
double Ymax = -INFINITY;
AF AFXmax;
AFXmax.Init(Dimension);
for (int j = 0; j < Dimension; j++) AFXmax.X[j] = 0;
for (int i = 0; i < N; i++)
{
double dij = Distance(*(af+id), *(af+i)), Yj = (af+i)->fitfunctionvalue();
if (dij != 0 && dij<visual && Yj >Ymax)
{
Ymax = Yj;
for (int j = 0; j < Dimension; j++)
AFXmax.X[j] = (af+i)->X[j];
}
}
double nf = 0;
for (int i = 0; i < N; i++)
{
double dmaxj = Distance(AFXmax,*(af+i));
if (dmaxj != 0 && dmaxj < visual)
nf++;
}
double Yi = (af + id)->fitfunctionvalue();
if (Ymax / nf > delta *Yi)
{
for (int j = 0; j < Dimension; j++)
(af+id)->X[j] = (af + id)->X[j] + r(random)*step*(AFXmax.X[j] - (af+id)->X[j]) / Distance(AFXmax, *(af+id));
}
else
prey(id);
}
void evaluate(int id)
{
if ((af + id)->fitfunctionvalue() > Bestfish.fitfunctionvalue())
{
for (int j = 0; j < Dimension; j++)
Bestfish.X[j] = (af + id)->X[j];
}
}
void run(int itetime)//运行函数
{
for (int k = 0; k < itetime; k++)
{
for (int i = 0; i < N; i++)
{
prey(i);
swarm(i);
follow(i);
evaluate(i);
}
std::cout << "第" << k + 1 << "次迭代最优位置为Bestfish:";
for (int j = 0; j<Dimension; j++)
{
if (j == Dimension - 1) std::cout << Bestfish.X[j] <<" "<<Bestfish.fitfunctionvalue()<< endl;
else std::cout << Bestfish.X[j] << ",";
}
}
std::cout << "迭代结束后最优位置为Bestfish:";
for (int j = 0; j<Dimension; j++)
{
if (j == Dimension - 1) std::cout << Bestfish.X[j] << " " << Bestfish.fitfunctionvalue() << endl;
else std::cout << Bestfish.X[j] << ",";
}
}
void shuchu()
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < Dimension; j++)std::cout << (af + i)->X[j] << " ";
std::cout << endl;
}
}
void doAFAS(int num, int Dim, double Step, double Visual, double Try_number, double Delta,int Itetime)
{
Init(num, Dim, Step, Visual, Try_number, Delta);
shuchu();
run(Itetime);
}
};
int main()
{
YUQUN yq;
while (true)
{
int num=0;
std::cout << "请输入迭代的次数:";
cin >> num;
if (num == 0)break;
else yq.doAFAS(10, 2, 0.3, 2.5, 5, 0.618, num);
}
system("pause");
return 0;
}
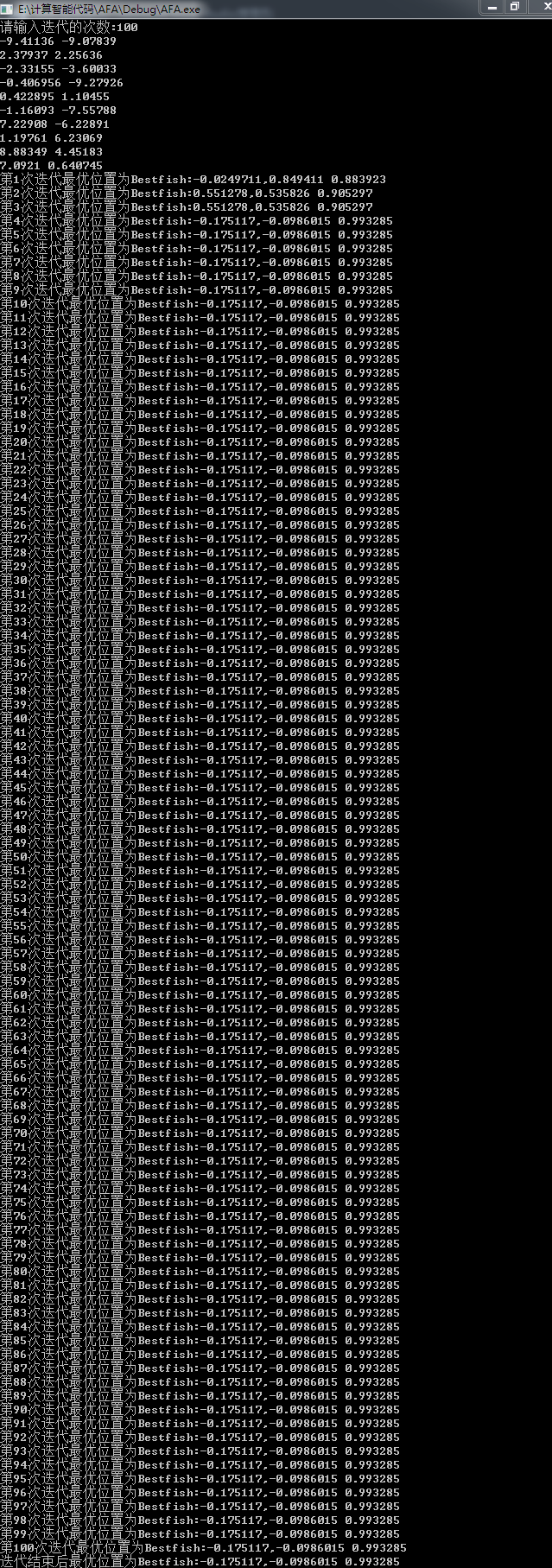
4.3 运行结果
5 算法特点
人工鱼群算法有良好的克服局部极值取得全局极值的能力,并且算法中只使用目标函数的函数值,无需目标函数的梯度值等特殊信息,对搜索空间具有一定的自适应能力。算法对初值无要求,对各参数的选择也不是很敏感。但该算法获取的仅仅是系统的满意解域,对于精确解的获取还需要进行适当的改进,一些改进的算法也被相继提出。
用人工鱼群算法解决离散优化问题时,该算法具有保持探索与开发平衡的能力较差和算法运行后期搜索的盲目性较大等缺点,从而影响了该算法搜索的质量和效率。