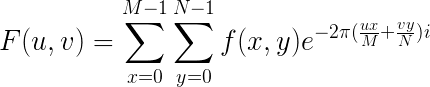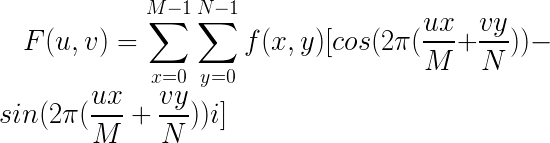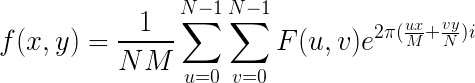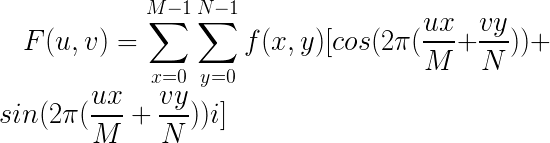傅里叶变换 二维离散傅里叶变换
1、介绍。
DFT:(Discrete Fourier Transform)离散傅里叶变换是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其DTFT的频域采样。在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT,也应当将其看作其周期延拓的变换。
1)、欧拉公式:
![]() ,其中i是虚数,即i的平方为-1。
,其中i是虚数,即i的平方为-1。
2)、二维离散傅里叶变换DFT公式:
N是二维数组的行数,M是二维数组的列数。u和v是转换后二维数组的位置,F(u,v)是转换后数组中相应位置的值。x和y是原二维数组的位置,f(x,y)是原数组中相应的值。
根据欧拉公式,也可以写成:
3)、二维离散傅里叶逆变换IDFT公式:
N是二维数组的行数,M是二维数组的列数。x和y是转换后二维数组的位置,f(x,y)是转换后数组中相应位置的值。u和v是原二维数组的位置,F(u,v)是原数组中相应的值。
根据欧拉公式,也可以写成:
2、生成随机的二维数组。
//f(x,y)=1+2x+8x^2+2y+3xy^2
private static double[][] getRandom2(int row, int column) {
double[][] arrays = new double[row][column];
for (int x = 0; x < row; x++) {
for (int y = 0; y < column; y++) {
double value = 1 + 2 * x + 8 * x * x + 2 * y + 3 * x * y * y;
arrays[x][y] = value;
}
}
return arrays;
}3、复数类。参考文章高数 复数的四则运算
package com.zxj.reptile.utils.number;
public class Complex {
private double real;//实数
private double image;//虚数
public Complex() {
real = 0;
image = 0;
}
public Complex(double real, double image) {
this.real = real;
this.image = image;
}
//加:(a+bi)+(c+di)=(a+c)+(b+d)i
public Complex add(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double newReal = this.real + real;
double newImage = this.image + image;
return new Complex(newReal, newImage);
}
//减:(a+bi)-(c+di)=(a-c)+(b-d)i
public Complex sub(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double newReal = this.real - real;
double newImage = this.image - image;
return new Complex(newReal, newImage);
}
//乘:(a+bi)(c+di)=(ac-bd)+(bc+ad)i
public Complex mul(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double newReal = this.real * real - this.image * image;
double newImage = this.image * real + this.real * image;
return new Complex(newReal, newImage);
}
//乘:a(c+di)=ac+adi
public Complex mul(double multiplier) {
return mul(new Complex(multiplier, 0));
}
//除:(a+bi)/(c+di)=(ac+bd)/(c^2+d^2) +((bc-ad)/(c^2+d^2))i
public Complex div(Complex complex) {
double real = complex.getReal();
double image = complex.getImage();
double denominator = real * real + image * image;
double newReal = (this.real * real + this.image * image) / denominator;
double newImage = (this.image * real - this.real * image) / denominator;
return new Complex(newReal, newImage);
}
//欧拉公式 e^(ix)=cosx+isinx
public static Complex euler(double x) {
double newReal = Math.cos(x);
double newImage = Math.sin(x);
return new Complex(newReal, newImage);
}
public double getReal() {
return real;
}
public void setReal(double real) {
this.real = real;
}
public double getImage() {
return image;
}
public void setImage(double image) {
this.image = image;
}
@Override
public String toString() {
String str = "";
if (real != 0) {
str += real;
} else {
str += "0";
}
if (image < 0) {
str += image + "i";
} else if (image > 0) {
str += "+" + image + "i";
}
return str;
}
}
4、二维离散傅里叶变换DFT代码。
public static Complex[][] getDft2(double[][] arrays) {
int M = arrays.length;
int N = arrays[0].length;
Complex[][] complexArrays = new Complex[M][N];
double flag = -2 * Math.PI;
for (int u = 0; u < M; u++) {
for (int v = 0; v < N; v++) {
//x-->M和y-->N的累加
Complex sum = new Complex();
for (int x = 0; x < M; x++) {
for (int y = 0; y < N; y++) {
//e^(-(2 * PI * (ux / M + vy / N)i)
double angle = flag * (u * x * 1.0 / M + v * y * 1.0 / N);
Complex complex = Complex.euler(angle);
//f(x) * e^(-(2 * PI * (ux / M + vy / N)i)
complex = complex.mul(arrays[x][y]);
sum = complex.add(sum);
}
}
complexArrays[u][v] = sum;
}
}
return complexArrays;
}5、二维离散傅里叶逆变换IDFT代码。
public static double[][] getInverseDft2(Complex[][] complexArrays) {
int M = complexArrays.length;
int N = complexArrays[0].length;
double[][] arrays = new double[M][N];
double flag = 2 * Math.PI;
for (int x = 0; x < M; x++) {
for (int y = 0; y < N; y++) {
//u-->M和v-->N的累加
Complex sum = new Complex();
for (int u = 0; u < M; u++) {
for (int v = 0; v < N; v++) {
//e^((2 * PI * (ux / M + vy / N)i)
double angle = flag * (u * x * 1.0 / M + v * y * 1.0 / N);
Complex complex = Complex.euler(angle);
//f(x) * e^((2 * PI * (ux / M + vy / N)i)
complex = complex.mul(complexArrays[u][v]);
sum = complex.add(sum);
}
}
//f(x) * e^((2 * PI * (ux / M + vy / N)i) / (M * N)
sum = sum.mul(1 * 1.0 / (N * M));
double realSum = sum.getReal();
arrays[x][y] = Math.round(realSum * 100) / 100.0;
}
}
return arrays;
}6、因为java的Arrays类没有提供二维数组是否相等的比较方法,所以自己写一个比较二维数组是否相等的方法。
public static boolean equals(double[][] a, double[][] b) {
if (a == null || b == null || a.length != b.length) {
return false;
}
for (int i = 0; i < a.length; i++) {
if (!Arrays.equals(a[i], b[i])) {
return false;
}
}
return true;
}7、流程。可以先将随机数组的大小设小点,然后将打印日志的代码开起来,这样子才会对流程有更多的了解。
public static void main(String[] args) {
System.out.println("------开始------");
long time = System.currentTimeMillis();
// testDft();//一维离散傅里叶变换
testDft2(10, 10);//二维离散傅里叶变换
System.out.println("花费时间 :" + (System.currentTimeMillis() - time));
System.out.println("------结束------");
}
private static void testDft2(int row, int column) {
System.out.println(String.format("二维数组共有%d行%d列", row, column));
//System.out.println("原数据: ");
double[][] arrays = getRandom2(row, column);
for (int x = 0; x < row; x++) {
for (int y = 0; y < column; y++) {
//System.out.print(arrays[x][y] + " ");
}
//System.out.println();
}
//System.out.println("离散傅里叶变换DFT: ");
Complex[][] dtfArrays = FourierUtils.getDft2(arrays);
for (int x = 0; x < row; x++) {
for (int y = 0; y < column; y++) {
//System.out.print(dtfArrays[x][y] + " ");
}
//System.out.println();
}
//System.out.println("逆离散傅里叶变换IDFT: ");
double[][] inverseDtfArrays = FourierUtils.getInverseDft2(dtfArrays);
for (int x = 0; x < row; x++) {
for (int y = 0; y < column; y++) {
//System.out.print(inverseDtfArrays[x][y] + " ");
}
//System.out.println();
}
System.out.print("二维离散傅里叶变换和逆离散傅里叶变换");
if (ArrayUtils.equals(arrays, inverseDtfArrays)) {
System.out.println("成功");
} else {
System.out.println("失败");
}
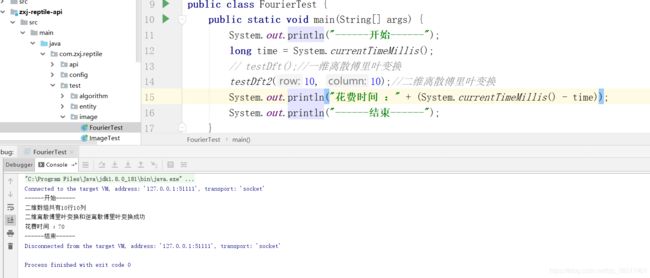
}8、结果。可以将生成随机二维数组的大小进行改变,也可以对生成随机数据的函数进行改变。会发现原数组和经过离散傅里叶变换DFT及逆离散傅里叶变换IDFT之后的数组是一模一样的,就可以验证出算法和公式是对的。我将打印的日志和结果截图一并给出来。
9、结论。
二维离散傅里叶因为涉及到4个嵌套循环,时间复杂度十分的大,所以在实际应用场景上得不到使用,现在的照片小的差不多也要500*500的大小,但是二维离散傅里叶处理大小60*60的时候,就已经显得十分的吃力了。