node2vec的一些理解

node2vec

node2vec也是一种网络嵌入的表示方法，它是基于DeepWalk的基础上进行改进的。主要改进的地方在于它在随机游走的过程中加入了一个权重，使得游走可以采用深度优先和广度优先的策略进行游走。

Search bias α

使得随机游走产生片偏差的最简单的方法是根据静态边缘权重$W_{v}x$进行采样，在未加权图的情况下$W_{vx}=1$，但是这并不能解释我们的网络结构，并且指导我们探索不同的网络邻居。此外，与BFS和DFS不同，BFS和DFS是分别适用于结构等价性和同质性的极端抽样范式，我们的随机游动应该适应这样一个事实：这些等价性的概念不是竞争的或排他的，而现实世界的网络通常表现出两者的混合。
所以我们定义了一个2阶随机游走，并且定义了两个参数分别是p和q用来指导我们进行随机游走。

假设我们有一个随机游走已经穿过了（t,v）节点并且现在暂时居住在如图所示的V节点。我们现在要考虑下一步怎么走，那么我们可以使用边（v,x）的转移概率${\Pi }_{vx}$用来引导我们从v的下一步怎么走。我们假定了一个转移概率${\Pi }_{v}x={\alpha }_{pq}(t,x)\ast W_{vx}$ 其中${\alpha }_{pq}(t,x)$定义如下：

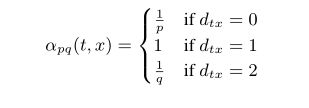
其中$d_{tx}$表示t和x之间的最短路径，注意的是$d_{tx}$的取值一定是{0,1,2}的其中一个，所以p，q两个参数能够很好的指导游走。
例如当终点为t时，我们相当于往回走了，不为t时我们则是向外游走或是向深游走。
返回参数 p：p代表我们游走时重复游走的可能性，如果我们把p设置为一个很高的值(> max(q,1))则可以用来确保我们有极小的可能性重复游走一个节点（除非下一个节点没有其他邻居）。这个策略鼓励我们适度探索，而不是产生冗余。另一方面，如果我们把p的值设为很小(< min(q,1))，则他会使得walk接近我们的起始位置。
In-Out参数 q:他更倾向于访问距离节点t更远的节点,这种行为反映了鼓励向外探索的DFS。然而，这里的一个本质区别是，我们在随机行走框架中实现了类似DFS的探索。

node2vec 算法流程

如上图所示，我们一开始主要是要进行我们的静态权重的赋值，用它来引导我们继续随机游走得到随机游走序列，然后我们将得到的序列利用skip-gram模型进行嵌入，最后得到嵌入矩阵。

    def _precompute_probabilities(self):
        """
        Precomputes transition probabilities for each node.
        """

        d_graph = self.d_graph

        nodes_generator = self.graph.nodes() if self.quiet \
            else tqdm(self.graph.nodes(), desc='Computing transition probabilities')

        for source in nodes_generator:

            # Init probabilities dict for first travel
            if self.PROBABILITIES_KEY not in d_graph[source]:
                d_graph[source][self.PROBABILITIES_KEY] = dict()

            for current_node in self.graph.neighbors(source):

                # Init probabilities dict
                if self.PROBABILITIES_KEY not in d_graph[current_node]:
                    d_graph[current_node][self.PROBABILITIES_KEY] = dict()

                unnormalized_weights = list()
                d_neighbors = list()

                # Calculate unnormalized weights
                for destination in self.graph.neighbors(current_node):

                    p = self.sampling_strategy[current_node].get(self.P_KEY,
                                                                 self.p) if current_node in self.sampling_strategy else self.p
                    q = self.sampling_strategy[current_node].get(self.Q_KEY,
                                                                 self.q) if current_node in self.sampling_strategy else self.q

                    if destination == source:  # Backwards probability
                        ss_weight = self.graph[current_node][destination].get(self.weight_key, 1) * 1 / p
                    elif destination in self.graph[source]:  # If the neighbor is connected to the source
                        ss_weight = self.graph[current_node][destination].get(self.weight_key, 1)
                    else:
                        ss_weight = self.graph[current_node][destination].get(self.weight_key, 1) * 1 / q

                    # Assign the unnormalized sampling strategy weight, normalize during random walk
                    unnormalized_weights.append(ss_weight)
                    d_neighbors.append(destination)

                # Normalize
                unnormalized_weights = np.array(unnormalized_weights)
                d_graph[current_node][self.PROBABILITIES_KEY][
                    source] = unnormalized_weights / unnormalized_weights.sum()

                # Save neighbors
                d_graph[current_node][self.NEIGHBORS_KEY] = d_neighbors

            # Calculate first_travel weights for source
            first_travel_weights = []

            for destination in self.graph.neighbors(source):
                first_travel_weights.append(self.graph[source][destination].get(self.weight_key, 1))
            first_travel_weights = np.array(first_travel_weights)
            d_graph[source][self.FIRST_TRAVEL_KEY] = first_travel_weights / first_travel_weights.sum()

具体代码实现如图所示，我们首先进入函数利用d_graph生成一个字典，在其中加入概率标签，然后我们通过循环节点以及节点的邻居对权重进行赋值，同时对我们的p，q进行策略的更改。最后的d_graph则是我们修改之后的带有我们设置的权重的重要参数，然后我们将d_graph带入到我们的游走序列生成的函数当中去。

def parallel_generate_walks(d_graph: dict, global_walk_length: int, num_walks: int, cpu_num: int,
                            sampling_strategy: dict = None, num_walks_key: str = None, walk_length_key: str = None,
                            neighbors_key: str = None, probabilities_key: str = None, first_travel_key: str = None,
                            quiet: bool = False) -> list:
    """
    Generates the random walks which will be used as the skip-gram input.

    :return: List of walks. Each walk is a list of nodes.
    """

    walks = list()

    if not quiet:
        pbar = tqdm(total=num_walks, desc='Generating walks (CPU: {})'.format(cpu_num))

    for n_walk in range(num_walks):

        # Update progress bar
        if not quiet:
            pbar.update(1)

        # Shuffle the nodes
        shuffled_nodes = list(d_graph.keys())
        random.shuffle(shuffled_nodes)

        # Start a random walk from every node
        for source in shuffled_nodes:

            # Skip nodes with specific num_walks
            if source in sampling_strategy and \
                    num_walks_key in sampling_strategy[source] and \
                    sampling_strategy[source][num_walks_key] <= n_walk:
                continue

            # Start walk
            walk = [source]

            # Calculate walk length
            if source in sampling_strategy:
                walk_length = sampling_strategy[source].get(walk_length_key, global_walk_length)
            else:
                walk_length = global_walk_length

            # Perform walk
            while len(walk) < walk_length:

                walk_options = d_graph[walk[-1]].get(neighbors_key, None)

                # Skip dead end nodes
                if not walk_options:
                    break

                if len(walk) == 1:  # For the first step
                    probabilities = d_graph[walk[-1]][first_travel_key]
                    walk_to = np.random.choice(walk_options, size=1, p=probabilities)[0]
                else:
                    probabilities = d_graph[walk[-1]][probabilities_key][walk[-2]]
                    walk_to = np.random.choice(walk_options, size=1, p=probabilities)[0]

                walk.append(walk_to)

            walk = list(map(str, walk))  # Convert all to strings

            walks.append(walk)

    if not quiet:
        pbar.close()

    return walks

生成游走的序列的代码如上图所示，我们可以看出将d_graph当中的概率取出，然后带入到np.random.choice这个函数当中去，这样我们就是按照一定的概率进行随机游走，而游走的概率是可以通过修改p,q两个参数进而进行修改的。最后我们则将我们得到的游走序列walks带入skip-gram模型进行训练，得到我们想要的嵌入矩阵。

    def fit(self, **skip_gram_params):
        """
        Creates the embeddings using gensim's Word2Vec.
        :param skip_gram_params: Parameteres for gensim.models.Word2Vec - do not supply 'size' it is taken from the Node2Vec 'dimensions' parameter
        :type skip_gram_params: dict
        :return: A gensim word2vec model
        """

        if 'workers' not in skip_gram_params:
            skip_gram_params['workers'] = self.workers

        if 'size' not in skip_gram_params:
            skip_gram_params['size'] = self.dimensions

        return gensim.models.Word2Vec(self.walks, **skip_gram_params)