人工智能----八数码难题解决 原理及算法实现
1.启发式搜索算法A
启发式搜索算法A,一般简称为A算法,是一种典型的启发式搜索算法。其基本思想是:定义一个评价函数f,对当前的搜索状态进行评估,找出一个最有希望的节点来扩展。
评价函数的形式如下:
f(n)=g(n)+h(n)
其中n是被评价的节点。
f(n)、g(n)和h(n)各自表述什么含义呢?我们先来定义下面几个函数的含义,它们与f(n)、g(n)和h(n)的差别是都带有一个“*”号。
g*(n):表示从初始节点s到节点n的最短路径的耗散值;
h*(n):表示从节点n到目标节点g的最短路径的耗散值;
f*(n)=g*(n)+h*(n):表示从初始节点s经过节点n到目标节点g的最短路径的耗散值。
而f(n)、g(n)和h(n)则分别表示是对f*(n)、g*(n)和h*(n)三个函数值的的估计值。是一种预测。A算法就是利用这种预测,来达到有效搜索的目的的。它每次按照f(n)值的大小对OPEN表中的元素进行排序,f值小的节点放在前面,而f值大的节点则被放在OPEN表的后面,这样每次扩展节点时,总是选择当前f值最小的节点来优先扩展。
过程A
①OPEN:=(s),f(s):=g(s)+h(s);
②LOOP: IF OPEN=( ) THEN EXIT(FAIL);
③n:=FIRST(OPEN);
④IF GOAL(n)THEN EXIT(SUCCESS);
⑤REMOVE(n,OPEN),ADD(n,CLOSED);
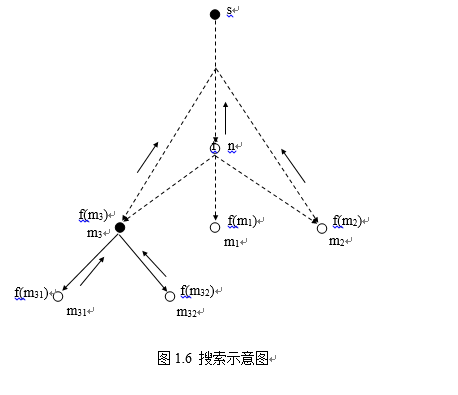
⑥EXPAND(n)→{mi},计算f(n,mi)=g(n,mi)+h(mi);g(n,mi)是从s通过n到mi的耗散值,f(n,mi)是从s通过n、mi到目标节点耗散值的估计。
·ADD(mj,OPEN),标记mi到n的指针。
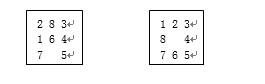
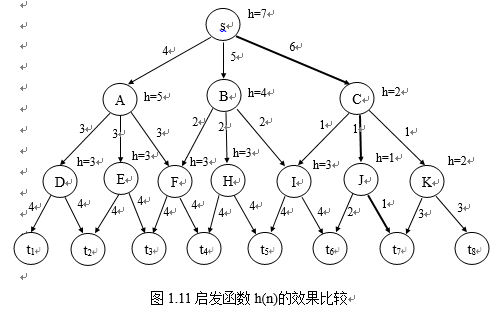
·IF f(n,mk) ·IF f(n,m1) ⑦OPEN中的节点按f值从小到大排序; ⑧GO LOOP; A算法同样由一般的图搜索算法改变而成。在算法的第7步,按照f值从小到大对OPEN表中的节点进行排序,体现了A算法的含义。 算法要计算f(n)、g(n)和h(n)的值,g(n)根据已经搜索的结果,按照从初始节点s到节点n的路径,计算这条路径的耗散值就可以了。而h(n)则依赖于启发信息,是与问题有关的,需要根据具体的问题来定义。通常称h(n)为启发函数,是对未来扩展的方向作出估计。 算法A是按f(n)递增的顺序来排列OPEN表的节点,因而优先扩展f(n)值小的节点,体现了好的优先搜索思想,所以算法A是一个好的优先的搜索策略。图1.6表示出当前要扩展节点n之前的搜索图,扩展n后新生成的子节点m1(∈{mj})、m2(∈{mk})、m3(∈{m1})要分别计算其评价函数值: f(m1)=g(m1)+h(m1) f(n,m2)=g(n,m2)+h(m2) f(n,m3)=g(n,m3)+h(m3) 然后按第6步条件进行指针设置和第7步重排OPEN表节点顺序,以便确定下一次要扩展的节点。 下面再以八数码问题为例说明A算法的搜索过程。 设评价函数f(n)形式如下: f(n)=d(n)+W(n) 其中d(n)代表节点的深度,取g(n)=d(n)表示讨论单位耗散的情况;取h(n)=W(n)表示以“不在位”的将牌个数作为启发函数的度量,这时f(n)可估计出通向目标节点的希望程度。 “不在位的将牌数”计算方法如下: 我们来看下面的两个图。 其中左边的图是8数码问题的一个初始状态,右边的图是8数码问题的目标状态。我们拿初始状态和目标状态相比较,看初始状态的哪些将牌不在目标状态的位置上,这些将牌的数目之和,就是“不在位的将牌数”。比较上面两个图,发现1、2、6和8四个将牌不在目标状态的位置上,所以初始状态的“不在位的将牌数”就是4,也就是初始状态的h值。其他状态的h值,也按照此方法计算。 图1.7表示使用这种评价函数时的搜索树,图中括弧中的数字表示该节点的评价函数值f。算法每一循环结束时,其OPEN表和CLOSED表的排列如下: OPEN表 CLODED表 初始化 (s(4)) 第一循环结束 (B(4) A(6) C(6)) 第二循环结束 (D(5) E(5) A(6) C(6) F(6)) 第三循环结束 (E(5) A(6) C(6) F(6) G(6) H(7)) 第四循环结束 (I(5) A(6) C(6) F(6) G(6) H(7) J(7)) 第五循环结束 (K(5) A(6) C(6) F(6) G(6) H(7) J(7)) 第六循环结束 (L(5) A(6) C(6) F(6) G(6) H(7) J(7) M(7)) 第七循环结束 第四步成功退出 ( ) (s(4)) (s(4) B(4)) (s(4) B(4) D(5)) (s(4) B(4) D(5) E(5)) (s(4) B(4) D(5) E(5) I(5)) (s(4) B(4) D(5) E(5) I(5) K(5)) 根据目标节点L返回到s的指针,可得解路径S(4),B(5),E(5),I(5),K(5),L(5) 当在算法A的评价函数中,使用的启发函数h(n)是处在h*(n)的下界范围,即满足h(n) ≤h*(n)时,则我们把这个算法称为算法A*。A*算法实际上是分支界限和动态规划原理及使用下界范围的h相结合的算法。当问题有解时,A*一定能找到一条到达目标节点的最佳路径。例如在极端情况下,若h(n)≡0(肯定满足下界范围条件),因而一定能找到最佳路径。此时若g≡d,则算法等同于宽度优先算法。前面已提到过,宽度优先算法能保证找到一条到达目标节点最小长度的路径,因而这个特例从直观上就验证了A*的一般结论。 一般地说对任意一个图,当s到目标节点有一条路径存在时,如果搜索算法总是在找到一条从s到目标节点的最佳路径上结束,则称该搜索算法是可采纳的(Admissibility)。A*就具有可采纳性。 下面来证明A﹡的可采纳性及若干重要性质。 定理1:对有限图,如果从初始节点s到目标节点t有路径存在,则算法A一定成功结束。 证明:设A搜索失败,则算法在第2步结束,OPEN表变空,而CLOSED表中的节点是在结束之前被扩展过的节点。由于图有解,令(n0=s,n1,n2,…,nk=t)表示某一解路径,我们从nk开始逆向逐个检查该序列的节点,找到出现在CLOSED表中的节点ni,即niÎCLOSED,ni+1ÏCLOSED(ni一定能找到,因为n0ÎDLOSED,nkÏCLOSED)。由于ni在CLOSES中,必定在第6步被扩展,且ni+1被加到OPEN中, 因此在OPEN表空之前,ni+1已被处理过。若ni+1是目标节点,则搜索成功,否则它被加入到CLOSED中,这两种情况都与搜索失败的假设矛盾,因此对有限图不失败则成功。[证毕] 因为A﹡是A的特例,因此它具有A的所有性质。这样对有限图如果有解,则A﹡一定能在找到到达目标的路径结束,下面要证明即使是无限图,A﹡也能找到最佳解结束。我们先证两个引理: 引理2.1:对无限图,若有从初始节点s到目标点t的一条路径,则A﹡不结束时,在OPEN中即使最小的一个f值也将增到任意大,或有f(n)>f﹡(s)。 在如下的证明中,隐含了两个假设:(1)任何两个节点之间的耗散值都大于某个给定的大于零的常量;(2)h(n)对于任何n来说,都大于等于零。 证明:设d﹡(n)是A﹡生成的搜索树中,从s到任一节点n最短路径长度的值(设每个弧的长度均为1),搜索图上每个弧的耗散值为C(ni,ni+1)(C取正)。令e=min C(ni,ni+1),则g﹡(n)≥d﹡(n)e。而g(n)≥g﹡(n)≥d﹡(n)e,故有: f(n)=g(n)+h(n)≥g(n)≥d﹡(n)e(设h(n)≥0) 若A﹡不结束,d﹡(n)y¥,f值将增到任意大。 设,M是一个定数,所以搜索进行到一定程度会有d﹡(n)>M,或,则 。 [证毕] 引理2.2:A*结束前,OPEN表中必存在f(n)≤f﹡(s)的节点(n是在最佳路径上的节点)。 证明:设从初始节点s到目标节点t的一条最佳路径序列为: (n0=s,n1,…,nk=t) 算法初始化时,s在OPEN中,由于A﹡没有结束,在OPEN中存在最佳路径上的节点。设OPEN表中的某节点n是处在最佳路径序列中(至少有一个这样的节点,因s一开始是在OPEN上),显然n的先辈节点np已在CLOSED中,因此能找到s到np的最佳路径,而n也在最佳路径上,因而s到n的最佳路径也能找到,因此有 f(n)=g(n)+h(n)=g*(n)+h(n) ≤g*(n)+h*(n)=f*(n) 而最佳路径上任一节点均有f*(n)=f*(s)(f*(s)是最佳路径的耗散值),所以f(n)≤f*(s)。[证毕] 定理2:对无限图,若从初始节点s到目标节点t有路径存在,则A*也一定成功结束。 3.启发函数与A*算法的关系 应用A*的过程中,如果选作扩展的节点n,其评价函数值f(n)=f*(n),则不会去扩展多余的节点就可找到解。可以想象到f(n)越接近于f*(n),扩展的节点数就会越少,即启发函数中,应用的启发信息(问题知识)愈多,扩展的节点数就越少。 定理4:有两个A*算法A1和A2,若A2比A1有较多的启发信息(即对所有非目标节点均有h2(n)>h1(n)),则在具有一条从s到t的隐含图上,搜索结束时,由A2所扩展的每一个节点,也必定由A1所扩展,即A1扩展的节点至少和A2一样多。 证明:使用数学归纳法,对节点的深度应用归纳法。 (1)对深度d(n)=0的节点(即初始节点s),定理结论成立,即若s为目标节点,则A1和A2都不扩展s,否则A1和A2都扩展了s(归纳法前提)。 (2)设深度d(n)≤=k,对所有路径的端节点,定理结论都成立(归纳法假设)。 (3)要证明d(n)=k+1时,所有路径的端节点,结论成立,我们用反证法证明。 设A2搜索树上有一个节点n(d(n)=k+1)被A2扩展了,而对应于A1搜索树上的这个节点n,没有被A1扩展。根据归纳法假设条件,A1扩展了n的父节点,n是在A1搜索树上,因此A1结束时,n必定保留在其OPEN表上,n没有被A1选择扩展,有 f1(n)≥f*(s),即g1(n)+h1(n)≥f*(s) 所以 h1(n)≥f*(s) - g1(n) (1) 另一方面A2扩展了n,有 f2(n)≤f*(s),即g2(n)+h2(n)≤f*(s) 所以 h2(n)≤f*(s)-g2(n) (2) 由于d=k时,A2扩展的节点,A1也一定扩展,故有 g1(n)≤g2(n)(因A1扩展的节点数可能较多) 所以 h1(n)≥f*(s) - g1(n)≥f*(s) - g2(n) (3) 比较式(2)、(3)可得:至少在节点n上有h1(n)≥h2(n),这与定理的前提条件矛盾,因此存在节点n的假设不成立。[证毕] 在定理4中所说的“有两个A*算法A1和A2”,指的是对于同一个问题,分别定义了两个启发函数h1和h2。这里要强调几点:首先,这里的A1和A2都是A*的,也就是说定义的h1和h2都要满足A*算法的条件。第二,只有当对于任何一个节点n,都有h2(n)>h1(n)时,定理才能保证用A2搜索所扩展的节点数≤用A1搜索所扩展的节点数。而如果仅是h2(n)≥h1(n)时(比定理的条件多了一个“等于”,而不只是单纯的“大于”),定理并不能保证用A2搜索所扩展的节点数≤用A1搜索所扩展的节点数。也就是说,如果仅是h2(n)≥h1(n),有等于的情况出现,可能会有用A2搜索所扩展的节点数反而多于用A1搜索所扩展的节点数的情况。第三,这里所说的“扩展的节点数”,是这样来计算的,同一个节点不管它被扩展多少次(在A算法的第六步,对于ml类节点,存在重新放回到OPEN表的可能,因此一个节点有可能被反复扩展多次,在后面我们会看到这样的例子),在计算“扩展的节点数”时,都只计算一次,而不管它被重复扩展了多少次。 该定理的意义在于,在使用A*算法求解问题时,定义的启发函数h,在满足A*的条件下,应尽可能地大一些,使其接近于h*,这样才能使得搜索的效率高。 由这个定理可知,使用启发函数h(n)的A*算法,比不使用h(n) (h(n)≡0)的算法,求得最佳路径时扩展的节点数要少,图1.11的搜索图例子可看出比较的结果。当h≡0时,求得最佳解路(s,C,J,t7),其f*(s)=8,但除t1~t8外所有节点都扩展了,即求出所有解路后,才找到耗散值最小的路径。而引入启发函数(设其函数值如图中节点旁边所示)后,除了最佳路径上的节点s,C,J被扩展外,其余的节点都没有被扩展。当然一般情况下,并不一定都能达到这种效果,主要在于获取完备的启发信息较为困难。 以上内容来源 马少平,朱小燕,人工智能,清华大学出版社 输入输出,需要命令行,VS下带命令行调试参见http://blog.csdn.net/bizer_csdn/article/details/48859931。 具体需求: 当初代码也是参考的,原作者http://blog.csdn.net/wsywl/article/details/5726617 原文地址:https://blog.csdn.net/bizer_csdn/article/details/51707756
2. 最佳图搜索算法A﹡(Optimal Search)
证明:假定A*不结束,由引理2.1有f(n)>f*(s),或OPEN表中最小的一个f值也变成无界,这与引理2.2的结论矛盾,所以A*只能成功结束。[证毕]
推论2.1:OPEN表上任一具有f(n)<f*(s)的节点n,最终都将被A*选作为扩展的节点。
定理3:若存在初始节点s到目标节点t的路径,则A*必能找到最佳解结束。
证明:
(1)由定理1、2知A*一定会找到一个目标节点结束。
(2)设找到一个目标节点t结束,而st不是一条最佳路径,即:
f(t)=g(t)>f*(s)
而根据引理2.2知结束前OPEN表上有节点n,且处在最佳路径上,并有f(n)≤f*(s),所以
f(n)≤f*(s)
推论3.1:A*选作扩展的任一节点n,有f(n)≤f*(s)。
证明:令n是由A*选作扩展的任一节点,因此n不会是目标节点,且搜索没有结束,由引理2.2而知在OPEN中有满足 的节点 。若n= ,则f(n)≤f*(s),否则选n扩展,必有 ,所以f(n)≤f*(s)成立。[证毕]#include "iostream"
#include "stdlib.h"
#include