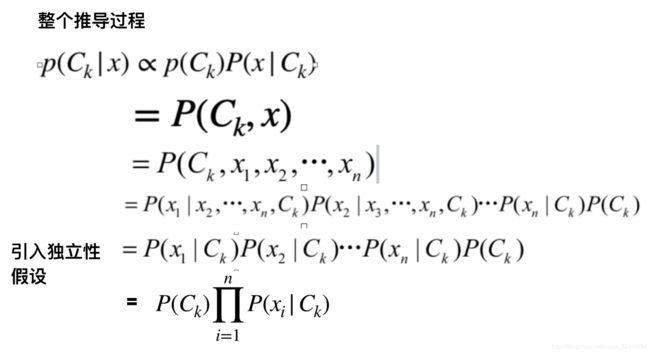机器学习：朴素贝叶斯

1 朴素贝叶斯应用场景

最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型（Naive Bayesian Model，NBM）。而常见朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。朴素贝叶斯主要运用于文本分类，垃圾邮件分类，信用评估，钓鱼网站检测等领域。

2 朴素贝叶斯相关公式

• 条件概率、概率乘法定理、全概率以及事件独⽴性（公式省略）。
• 贝叶斯公式
  • $P(B_i|A)=\frac{P(B_{i}A)}{P(A)}=\frac{P(A|B_i)P(B_i)}{{\sum }_{j=1}^{n}P(A|B_j)P(B_j)}$
• 贝叶斯定理常用形态
  • $P(A)=P(A|B)P(B)+P(A|\overline{B})P(\overline{B})$
  • $P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A|B_i)P(B_i)}{P(A|B)P(B)+P(A|\overline{B})P(\overline{B})}$
• 朴素贝叶斯公式推导过程（朴素的含义是事件具有独立性）
  • $p(C_k|x)=\frac{p(C_k)P(x|C_k)}{P(x)}$
  • 当数据是确定的时候 $C_k$，$P(x)$定值
    

3 sklearn库中朴素贝叶斯运用

3.1 伯努利朴素贝叶斯

• sklearn.naive_bayes.BernoulliNB
• 数据库特征符合二项分布。
• 参数：
  • alpha : float, optional (default=1.0) 拉普拉斯平滑系数
  • fit_prior:bool, optional (default=True)是否从数据集中学习先验概率,如果false,就用平均概率值
  • class_prior:array-like, size=[n_classes,], optional (default=None）先验概率的值,认为指定先验概率.如果指定了,就按照指定的先验概率来进行计算.
• 属性：
  • class_count_ :array, shape = [n_classes] 没个类别有多少个样本
  • class_log_prior_:array, shape = [n_classes] 每个类别先验概率的对数值
  • classes_array, shape (n_classes,) 有哪些类别标签
  • feature_count_ :array, shape = [n_classes, n_features] 特征级数
  • feature_log_prob_array, shape = [n_classes, n_features] 给定类的特征的经验对数概率
  • n_features_ :int 每个样本的特征个数

3.2 多项式朴素贝叶斯

• sklearn.naive_bayes.MultinomialNB
• 假设特征符合多项式分布，常用与文本分类，特征是单词，值是单词出现的次数。
• 参数属性同上。

3.3 高斯朴素贝叶斯

• sklearn.naive_bayes.GaussianNB
• 有些特征可能是连续型变量，高斯朴素贝叶斯模型假设这些特征属于某个类别的观测值符合高斯分布。
• 参数：
  • priors :array-like, shape (n_classes,)* 类别的先验概率
  • var_smoothing : float, optional (default=1e-9) 方差平滑系数

详细介绍查看文档naive_bayes.

4 代码

4.1建模

# 数据集: 加载手写数字识别数据集
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

# 调用函数载入数据集
digits = load_digits()

#查看数据集信息
digits.keys()

dict_keys(['data', 'target', 'target_names', 'images', 'DESCR'])

print(digits.DESCR) # 数据集详细信息描述
digits.target_names # 数据集中有哪些标签
digits.data[0] # 第一个样本的数据
digits.images[0] # 第一个样本的images

# 将数字矩阵转换成图像进行观察 imshow函数示范 - images_show
# 对模型无用，仅展示用法
# cmap 参数: 颜色映射方案, 黑白的映射方案
index = 100
plt.imshow(digits.images[index],cmap = 'binary')

输出图片

# 拆分训练集和测试集
X = digits.data
y = digits.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
   X, y, test_size=0.3, random_state=0)

# 导入三个模型
from sklearn.naive_bayes import BernoulliNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score # 交叉验证

# 模型实例化
bnb = BernoulliNB()
mnb = MultinomialNB()
gnb = GaussianNB()
# 使用默认参数

# 训练模型
bnb.fit(X_train,y_train)
mnb.fit(X_train,y_train)
gnb.fit(X_train,y_train)

# 评估模型
# 分别看一下三个模型,在训练集和测试集的分数
print('bnb模型训练集分数:',bnb.score(X_train,y_train))
print('bnb模型测试集分数:',bnb.score(X_test,y_test))
print('-'*40)
print('mnb模型训练集分数:',mnb.score(X_train,y_train))
print('mnb模型测试集分数:',mnb.score(X_test,y_test))
print('-'*40)
print('gnb模型训练集分数:',gnb.score(X_train,y_train))
print('gnb模型测试集分数:',gnb.score(X_test,y_test))

输出3种模型的分数
bnb模型训练集分数: 0.8647573587907716
bnb模型测试集分数: 0.8592592592592593
----------------------------------------
mnb模型训练集分数: 0.9029435163086714
mnb模型测试集分数: 0.9166666666666666
----------------------------------------
gnb模型训练集分数: 0.8687350835322196
gnb模型测试集分数: 0.8555555555555555

4.2 BernoulliNB调参

bnb_train_score = []
bnb_test_score = []
bnb_cross_score = []
alpha=np.arange(0.01,1.01,0.01)
# 因为模型只有一个参数可调,所以这里我们使用学习曲线进行调参
# alpha=1.0,  0.01 -- 1  0.01,0.02,0.03---1
for i in alpha:
    # 建立模型
    bnb = BernoulliNB(alpha=i)
    # 训练模型
    bnb.fit(X_train,y_train)
    bnb_train_score.append( bnb.score(X_train,y_train) )
    bnb_test_score.append(bnb.score(X_test,y_test) )
    cross = cross_val_score(bnb,X_train,y_train,cv=5).mean() 
    bnb_cross_score.append(cross) # 保存交叉验证分数

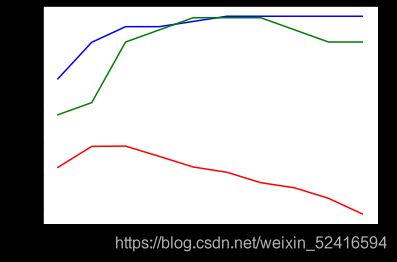
# 绘制出学习曲线的变化
plt.plot(np.arange(0.01,1.01,0.01),bnb_train_score ,color='blue')
plt.plot(np.arange(0.01,1.01,0.01),bnb_test_score ,color='green')
plt.plot(np.arange(0.01,1.01,0.01),bnb_cross_score ,color='red')

输出下图

有点过拟合

# 继续缩小范围
# 1,0.1,0.01,0.001,0.0001 ,  10-9

bnb_train_score = []
bnb_test_score = []
bnb_cross_score = []
n = 1
for i in range(10):
    # 建立模型
    bnb = BernoulliNB(alpha=n)
    # 训练模型
    bnb.fit(X_train,y_train)
    bnb_train_score.append( bnb.score(X_train,y_train) )
    bnb_test_score.append(bnb.score(X_test,y_test) )
    cross = cross_val_score(bnb,X_train,y_train,cv=5).mean()
    bnb_cross_score.append(cross) # 保存交叉验证分数
    n /= 10

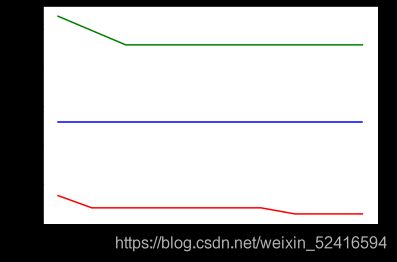
# 绘制出学习曲线的变化
plt.plot(bnb_train_score ,color='blue')
plt.plot(bnb_test_score ,color='green')
plt.plot(bnb_cross_score ,color='red');
plt.xlabel(pow(0.1,np.arange(10)))

max(bnb_cross_score)

0.8544722213508174
确定 alpha参数 = 0.01最佳，但模型仍然不太理想。

4.3 MultinomialNB调参

# MultinomialNB
# 调参范围

mnb_train_score = []
mnb_test_score = []
mnb_cross_score = []
n = 1
for i in range(10):
    # 建立模型
    mnb = MultinomialNB(alpha=n)
    # 训练模型
    mnb.fit(X_train,y_train)
    mnb_train_score.append( mnb.score(X_train,y_train) )
    mnb_test_score.append(mnb.score(X_test,y_test) )
    cross = cross_val_score(mnb,X_train,y_train,cv=5).mean()
    mnb_cross_score.append(cross) # 保存交叉验证分数
    n /= 10
    

# 绘制出学习曲线的变化
plt.plot(mnb_train_score ,color='blue')
plt.plot(mnb_test_score ,color='green')
plt.plot(mnb_cross_score ,color='red')
plt.xlabel(pow(0.1,np.arange(10)))

测试集比训练集高 。

mnb_train_score = []
mnb_test_score = []
mnb_cross_score = []

for i in np.arange(0.1,10.1,0.1):
    # 建立模型
    mnb = MultinomialNB(alpha=i)
    # 训练模型
    mnb.fit(X_train,y_train)
    mnb_train_score.append( mnb.score(X_train,y_train) )
    mnb_test_score.append(mnb.score(X_test,y_test) )
    cross = cross_val_score(mnb,X_train,y_train,cv=5).mean()
    mnb_cross_score.append(cross) # 保存交叉验证分数

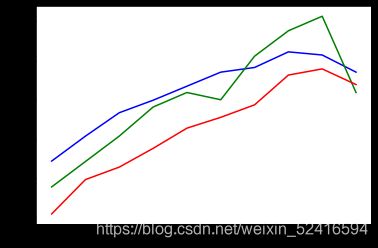
# 绘制出学习曲线的变化
plt.plot(np.arange(0.1,10.1,0.1),mnb_train_score ,color='blue')
plt.plot(np.arange(0.1,10.1,0.1),mnb_test_score ,color='green')
plt.plot(np.arange(0.1,10.1,0.1),mnb_cross_score ,color='red');

np.max(mnb_cross_score)
# 找序列中最大值所对应的索引值
np.argmax(mnb_cross_score)
mnb_cross_score[46]
# 索引46,在参数序列中对应的参数值
np.arange(0.1,10.1,0.1)[46]

4.7

4.4 GaussianNB调参

# GaussianNB
# 调参范围
# 1,0.1,0.01,0.001,0.0001 ,  10-9

gnb_train_score = []
gnb_test_score = []
gnb_cross_score = []
n = 1e-9 # 从小到大循环
for i in range(10):
    # 建立模型
    gnb = GaussianNB(var_smoothing=n)
    # 训练模型
    gnb.fit(X_train,y_train)
    gnb_train_score.append( gnb.score(X_train,y_train) )
    gnb_test_score.append(gnb.score(X_test,y_test) )
    cross = cross_val_score(gnb,X_train,y_train,cv=5).mean()
    gnb_cross_score.append(cross) # 保存交叉验证分数
    print(n)
    n *= 10
    

# 绘制出学习曲线的变化
plt.plot(gnb_train_score ,color='blue')
plt.plot(gnb_test_score ,color='green')
plt.plot(gnb_cross_score ,color='red');

根据曲线,在参数为1e-9*8=0.1中得到了最高值

np.max(gnb_cross_score)

# 我们在0.1的前后范围内再次进行调参,看看有没有更好的结果

gnb_train_score = []
gnb_test_score = []
gnb_cross_score = []

# 0.01 , 2  0.01
for i in np.arange(0.01,1,0.01):
    # 建立模型
    gnb = GaussianNB(var_smoothing=i)
    # 训练模型
    gnb.fit(X_train,y_train)
    gnb_train_score.append( gnb.score(X_train,y_train) )
    gnb_test_score.append(gnb.score(X_test,y_test) )
    cross = cross_val_score(gnb,X_train,y_train,cv=5).mean()
    gnb_cross_score.append(cross) # 保存交叉验证分数

# 绘制出学习曲线的变化
plt.plot(np.arange(0.01,1,0.01),gnb_train_score ,color='blue')
plt.plot(np.arange(0.01,1,0.01),gnb_test_score ,color='green')
plt.plot(np.arange(0.01,1,0.01),gnb_cross_score ,color='red');

np.max(gnb_cross_score) # 有所增加

0.9173462706957286

np.argmax(gnb_cross_score)

1

# 索引为1 ,对应的参数值为
np.arange(0.01,1,0.01)[1]

0.02

4.5 结论

• 选用高斯朴素贝叶斯 GaussianNB
• 参数var_smoothing = 0.02中,交叉验证分数达到最高值,为0.917

- END -