【题解+解题报告】2020浙江工业大学程序设计迎新赛——决赛(除了E和M以外)
写在前面的话:
这次比赛的题目把我惊艳到了,题目质量非常高,给出题人点个赞!
A
知识点:模拟。
参考cf难度:1500
这道题其实读懂题,按题意模拟就可以了。数据很小,所以每次操作直接排序即可。要注意的是每个学生能力值改变的时间点不要搞错了。
复杂度: O ( n 2 l o g n ) O(n^2logn) O(n2logn)
#includeB
知识点:状压搜索/DFS
参考cf难度:2100
第一次想到的算法是贪心:枚举每个度数 i i i,先顺时针到 i i i再逆时针;或者先逆时针到 i i i再顺时针,结果wa了,甚至一度怀疑题目出问题了。
后面发现这个算法是错的,有可能出现先逆时针,再顺时针,再逆时针的情况(因为每个点的 t t t是不同的,所以不能简单的去贪心)。正确做法是枚举每一次选择顺时针或者逆时针,这样一共有 n n n次决策,总决策方案就是 2 n 2^n 2n种。
复杂度: O ( n ∗ 2 n ) O(n*2^n) O(n∗2n)
#include
for(i=0;i<1<<n;i++){
int templ=l,tempr=r,st=y;
ll p=i,sum=0,ma=0;
for(j=0;j<n;j++){
if(p&1){
sum+=(st-a[templ].w+360)%360*x;
// cout<<"1:"<
ma=max(ma,sum+a[templ].v);
st=a[templ].w;
templ=(templ-1+n)%n;
}
else{
sum+=(a[tempr].w-st+360)%360*x;
// cout<<"2:"<
ma=max(ma,sum+a[tempr].v);
st=a[tempr].w;
tempr=(tempr+1)%n;
}
p/=2;
}
// cout<<"p"<
mi=min(mi,ma);
}
cout<<mi;
// cout<
}
C
知识点:前缀和预处理
参考cf难度:1600
这道题要求的是距离不大于k的所有01对的数量。那么对于每个0/1而言,只需要知道距离它不超过k的所有1/0的数量,然后前缀和预处理就可以O(1)查询了。
复杂度:O(n)
#include
ll cnt=0;
for(i=0;i<s.length();i++){
if(s[i]=='0'){
cnt+=sum2[min(i+k+1,n)]-sum2[max(i-k,0LL)];
// cout<
}
else{
cnt+=sum1[min(i+k+1,n)]-sum1[max(i-k,0LL)];
}
// cout<
}
cout<<cnt/2;
}
D
知识点:贪心
参考cf难度:800
签到题。很明显当且仅当摸大鱼体力不超过摸小鱼两倍的时候选择摸大鱼,否则一定会摸小鱼。注意如果 n n n是奇数那么最后要用小鱼补全。
复杂度 O ( T ) O(T) O(T)
#includeF
知识点:计算几何/(三分)
参考cf难度:1900
这道题官方题解非常优秀,不过我是用三分卡过去的。
当两个点开始运动之后,很明显距离是先变小、后变大这一过程,满足可三分的性质。
由于double可能会卡精度,所以只要三分足够多次就可以了。
复杂度: O ( T l o g ? ) O(Tlog?) O(Tlog?)
#include
double l=0,r=min(len1,len2);
for(i=0;i<1000;i++){
double lmid=l+(r-l)/3,rmid=l+2*(r-l)/3;
if(f(lmid)<f(rmid))r=rmid;
else l=lmid;
}
printf("%.2f\n",f(l));
}
}
G
知识点:概率论
参考cf难度:1300
看到数据范围这么小,直接套期望的公式就可以了:
E = ∑ i = 1 n p ( i ) ∗ i E=\sum_{i=1}^n p(i)*i E=∑i=1np(i)∗i
其中 p ( i ) p(i) p(i)用古典概型的条件概率直接求就可以。
复杂度: O ( n ) O(n) O(n)
#includeH
知识点:贪心
参考cf难度:1500
这道题其实很简单,不过由于读题劝退所以前2h居然没有一发提交hhh
题目的公式已经告诉你了,那么可以根据每个怪的属性求出最大的伤害,然后求出击杀次数,之后按次数从小到大选择就可以模拟了。
不过这道题出的不好的一点的是居然存在血量为0的怪,理论上无视它就可以了(
复杂度: O ( T n l o g n ) O(Tnlogn) O(Tnlogn)
#include
// return 0;
int b;
int n,r,l,m;
cin>>t;
while(t--){
ll sum=0;
cin>>n>>m;
int c1,k1,c2,k2;
cin>>c1>>k1>>c2>>k2;
for(i=0;i<n;i++)cin>>a[i].hp;
for(i=0;i<n;i++)cin>>a[i].d;
for(i=0;i<n;i++){
int dmg=max(0,max(c1-k1*a[i].d,c2-k2*a[i].d));
if(dmg==0){
a[i].val=1e9;continue;}
// cout<
a[i].val=a[i].hp/dmg+(a[i].hp%dmg!=0);
}
sort(a,a+n,cmp);
for(i=0;i<n&&sum+a[i].val<=m;i++)sum+=a[i].val;
cout<<i<<endl;
}
}
I
知识点:思维
参考cf难度:1400
非常巧妙的一道题。这道题的关键就是构造出(或者猜出) n ≥ 2 n≥2 n≥2时最小面积一定是1。
具体的构造方法参考下图:
 复杂度: O ( T ) O(T) O(T)
复杂度: O ( T ) O(T) O(T)
#includeJ
知识点:dp、贪心
参考cf难度:2200
非常好的一道题。题意大概这样:将每个1变成0的条件是:这个1的前面都没有0。并且变完了之后会把这个1前面 k k k个字符都变成1。
因此可以得到dp方程:
d p [ i ] = 1 + ∑ j = 1 k d p [ i − j ] dp[i]=1+\sum_{j=1}^kdp[i-j] dp[i]=1+∑j=1kdp[i−j]
这个方程可以简化成这样:
前 k k k项dp项之和与 d p [ i − 1 ] dp[i-1] dp[i−1]也可以建立某种联系,经过推导后可以得出:
d p [ i ] = 2 ∗ d p [ i − 1 ] − d p [ i − k − 1 ] dp[i]=2*dp[i-1]-dp[i-k-1] dp[i]=2∗dp[i−1]−dp[i−k−1]
有 t t t次交换的机会,很明显的,一定优先交换右边的1,因为右边的1会带来更多的次数。
之后将预处理出的dp数组进行求和就可以了。
复杂度: O ( n + t ) O(n+t) O(n+t)
#include
int t,i,j,k;
// for(i=999990;i<=1000000;i++)cout<
// return 0;
int b;
int n,r,l,m;
int x,y;
cin>>n>>k>>t;
string s;
cin>>s;
dp[1]=1;
for(i=2;i<=k+1;i++){
dp[i]=dp[i-1]*2%mod;
}
for(i=k+2;i<=1e5;i++){
dp[i]=2*dp[i-1];
if(i>k+1)dp[i]-=dp[i-k-1];
dp[i]=(dp[i]+mod)%mod;
}
//for(i=1;i<=10;i++)cout<
while(t){
for(i=s.length()-1;i>=0;i--){
if(s[i]=='1')break;
}
for(;i>=0;i--)if(s[i]=='0')break;
if(i<0)break;
for(;i<s.length()-1;i++){
if(s[i+1]=='1')swap(s[i],s[i+1]),t--;
if(!t)break;
}
if(!t)break;
}
ll sum=0;
for(i=0;i<s.length();i++){
sum+=(s[i]=='1')*dp[i+1];
sum%=mod;
}
cout<<sum;
}
K
知识点:博弈
参考cf难度:1300
当n小于3时,显然后手胜。
n≥3时,一定先手胜。证明如下:
若n为奇数,第一次这样画:
 后面每次对方怎么画,自己在对称的另一边画同样的形状即可。
后面每次对方怎么画,自己在对称的另一边画同样的形状即可。
若n为偶数,第一次这样画:
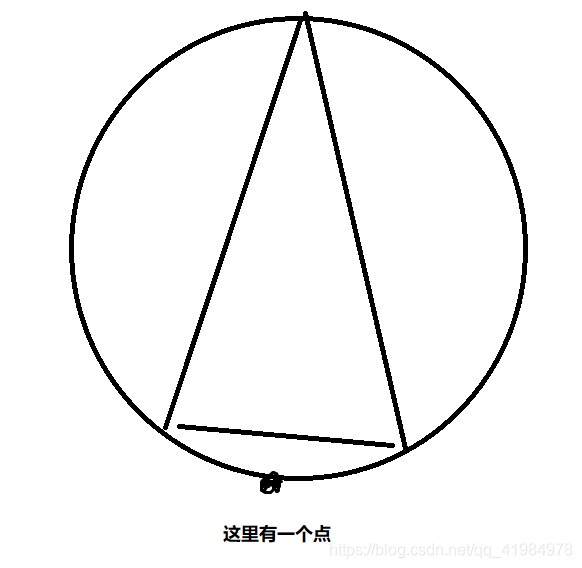
然后用同样的方式,对称着画,保证每次画完都是轴对称状态,这样第一次无法画的一定是对方。
复杂度: O ( T ) O(T) O(T)
#includeL
知识点:数论,构造算法
参考cf难度:1900
初始序列为1,2,3……n。第一次某个数加1,第二次某个数加2,以此类推,求操作数最小的次数使得gcd大于1,并输出字典序最小的序列。
首先可以证明,最小的操作数为n-1。证明如下:
必要性:
若n是2的倍数,那么把所有数变成2的倍数需要n-1次。若n不是2的倍数,则需要n次。
若n%3=0,那么把所有数变成3的倍数需要n-1次。若n%3=1,那么无论如果不能让他们都变成3的倍数。若n%3=2,那么把所有数变成3的倍数需要n次。
一般地,若我们要让所有数的gcd变成p,首先要让1,…,p-1所有数变成p的倍数,然后遇到一个p的时候操作在模p意义下是无效的。所以至少需要n-1次。
充分性:
设有1,2…n的初始序列,我们让1加到n-1,2加到n-2……以此类推,n-1加到1上面,这样n-1次操作所有数都变成n了。
证明完毕。
所以这道题的关键是怎么找到字典序最小的n-1的序列。
假设我们要让所有数的gcd变成p,我们可以让1加到p-1上,2加到p-2上……p-1加到1上,这次第一个数变成p了,可以再让他加p(这样字典序最小);之后让p+1加到2p-1上……以此类推。最终我们的序列是p-1,p-2…1,1,2p-1,2p-2…p+1,1,3p-1…
那么如果让字典序最小,很明显就是让p最小。而p又必须是n的因子(这样才能n-1次操作完成),所以这道题只要求出n除了1以外最小的因子就可以了。这个操作可以通过线性筛进行预处理。
复杂度 O ( n ) O(n) O(n)
#include
// return 0;
int b;
int n,r,l;
cin>>t;
while(t--){
scanf("%d",&n);
int p=tong[n];
if(p==0)p=n;
// if()
if(n==1)printf("1\n1\n");
else{
printf("%d\n",n-1);
for(i=p;i<=n;i+=p){
for(j=i-1;j>i-p;j--){
if(!(i==p&&j==i-1))printf(" ");
printf("%d",j);
}
if(i!=n)printf(" 1");
}
printf("\n");
}
}
}