CS224W笔记-第十课

CS224W笔记-第十课：深度图生成模型

第九课是一个助教的实践课，所以就不写讲义了。

回顾上节课的内容

GNN完成了把图结构转化到向量空间，即称为一个$Encoder$。其基本思路是通过不同的局部图结构构成的计算图，使用共享的参数构建深度网络，把邻居结点的特征层层聚合到一个节点，完成embedding的计算。基于这个思路，GCN和GraphSage使用不同的聚合方法构建了深度图神经网络。

这个编码的过程可以用下图来示意：
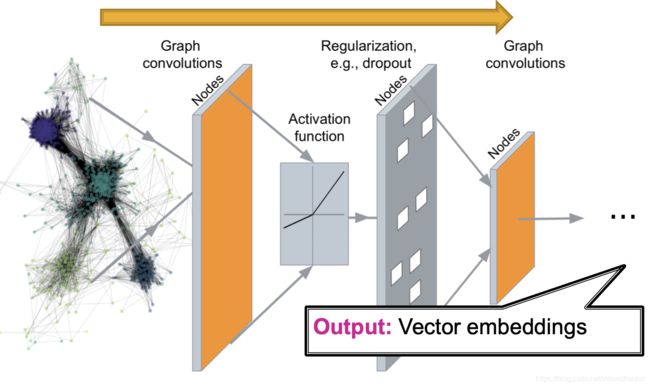第九课的内容就是把这个过程反过来，即从右侧向左侧实现一个解码器$Decoder$。

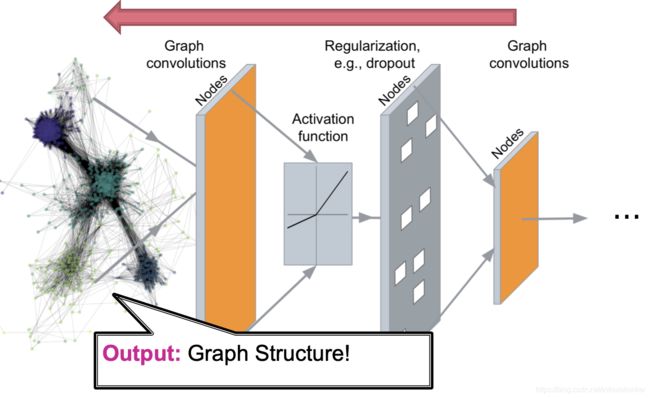
图生成问题定义

给定一系列真实的图，使用模型生成人造的图。问题的核心就是：

1. 如何评估一个模型；
2. 如何用这个模型生成图。

两种类型的图生成任务

1. 现实图生成：生成和给定的一系列图想类似的图。这是这节课主要介绍的。
2. 特定目的的图生成：生产针对特定目标或限制进行优化的图。

图生成的挑战

• 需要生成的数据量($n$个点就需要生成$n^2$个值)很大，而且生成的图的大小也差别很大。
• 生成的结果不具有唯一性，改变点的顺序不会改变图，但输出结果却会变($n$个点的图，会有$n!$种邻接矩阵的表示方法)。这让优化结果很困难。
• 生成的结果具有复杂的依赖性，因为边的生成可能要依赖全图的结构。

问题设定：

• 训练数据是来自$p_{data}(G)$采样的一批图。
• 目标是：
  1. 学习到一个模型分布$p_{model}(G)$
  2. 由此分布采样获得的生成图

图生成的机器学习基本方法——生成模型概述

设定：
从一系列数据样本$\{x_i\}$中学习一个生成模型。

• $p_{data}(x)$是这些数据的分布，真实的分布情况我们永远不可能知道。但是数据样本是从这个分布里采样出来的，即$x_i\backsim p_{data}(x)$
• $p_{model}(x;\theta )$是由参数$\theta$定义的模型。我们用它来近似$p_{data}(x)$。

目标：

• 使得$p_{model}(x;\theta )$尽量地接近$p_{data}(x)$。
• 同时，也让我们能从$p_{model}(x;\theta )$采用出需要数据点。

方法：最大似然估计

为了实现让$p_{model}(x;\theta )$尽量接近$p_{data}(x)$，可以使用机器学习里最常见的最大似然估计的方法，具体的公式为：$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}{\mathbb{E}}_{x\backsim p_{data}}\mathrm{l}\mathrm{o}\mathrm{g}{p}_{model}(x|\theta )$$
即，找到${\theta }^{\ast }$，从而让来自分布$p_{data}$的数据点$x_i$，在所有的$\theta$中，${\sum }_i\mathrm{l}\mathrm{o}\mathrm{g}{p}_{model}(x_i;{\theta }^{\ast })$的值最大。

有了$p_{model}(x;\theta )$，采样的方法是：

• 从某个简单的噪声分布里采样一些值，即$z_i\backsim N(0,1)$;
• 然后使用一个函数$f(\cdot )$把$z_i$转换成数据点$x_i$，即$x_i=f(z_i;\theta )$，其中$x_i$符合我们想拟合的复杂分布。
  对于转换函数$f(\cdot )$，可以使用一个神经网络来实现，用已有的样本数据$x_i$来训练。

深度学习生成模型
Jure没有讲的一页关于深度学习的生成模型的结构如下图。CS231n里面曾经介绍过这个分类法，其中介绍了PixelRNN和GAN。
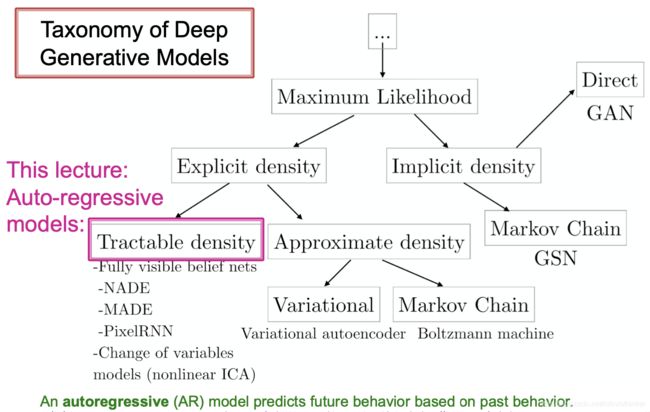后面要说的模型就是“自回归模型”：用过去的行为来预测未来的行为，一个模型完成了密度估计和采样新样本两个动作。

自回归模型会应用链式规则，即它是一个条件概率分布的乘积：$$p_{model}(x;\theta )=\prod _{t=1}^n{p}_{model}(x_t|x_1,\cdots ,x_{t-1};\theta )$$
这样就把生成模型变成了一个生成序列。每个$t$对应着生成序列的一个步骤。

图生成模型——GraphRNN

这是Jure的学生在2018年ICML里面发一篇论文GraphRNN: Generating Realistic Graphs with Deep Auto-regressive Models

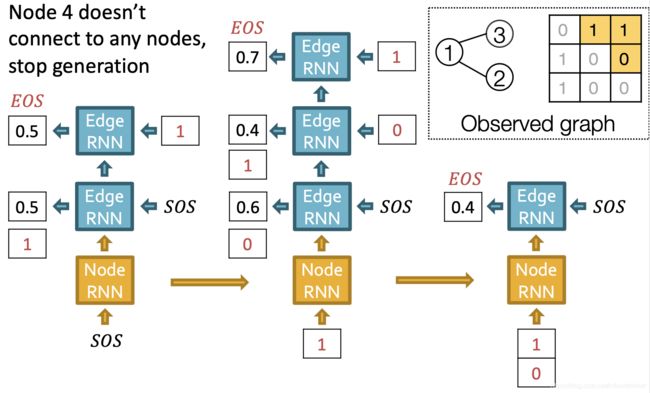
GraphRNN的基本思路是把图生成的过程变成一个序列$S^{\pi }$，其中$\pi$是指的图的节点的一个固定的序列。如下图所示：
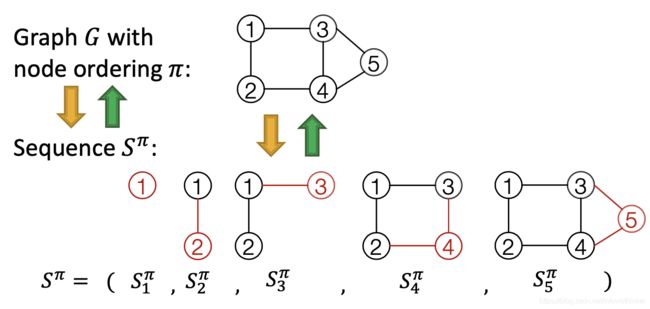在上图中，生成的图包含5个节点，各自一个编号。生成的过程是从节点1开始，每个步骤增加1个新节点和新节点与原有节点之间的边。按照这个方法，整个生成的序列包含两个层面的任务：

1. 节点层面：每步增加1个节点，直到出现EOS(End of Sequence，结束标志)
2. 边层面：新增加1个节点后，增加边，直到完成和所有已经存在的点之间的边构建(有边或无边)。

这样在确定一个节点顺序后，图生成就等于是一个序列的序列。

那么整个图生成过程就转变成了如何通过学习来获得这个生成的过程。需要学习两个层面的序列，即节点层面和边层面。对于序列数据的学习，比较自然的方法就是使用RNN来训练一个参数共享的模型。

GraphGNN设置

这里如果对RNN比较熟悉的话，就能比较好地理解GraphRNN的思路。总体网络架构如下：
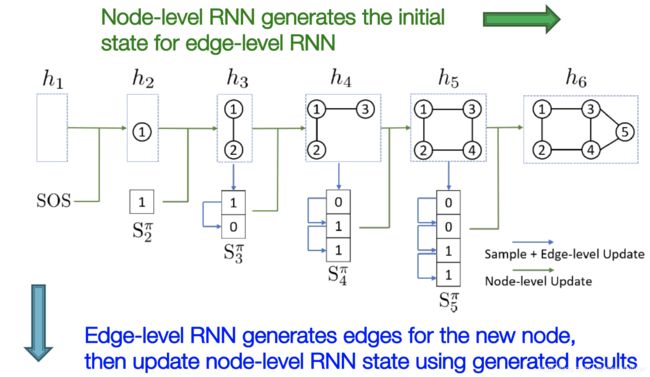其中，每个方格就是一个RNN的模块，权重共享，如下图所示：

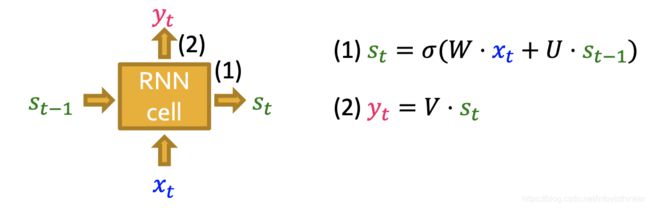
而RNN的输入和输出结构展开来看就是：
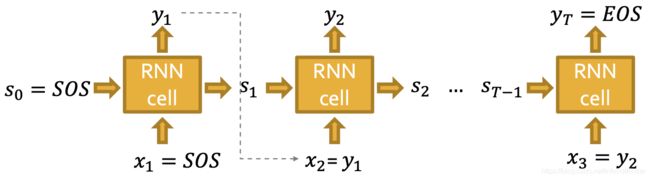这是针对节点级别的顺序，其中需要有SOS(Start of Sequence)和EOS(End of Sequence)。而每个$y$则可以认为是另外一个这个的RNN单元，但是生成的是边级别的顺序。一点不同是，边级别的生产可以没有SOS和EOS，因为每个新节点可以生成的最多的边是固定数量的。

对于每个步骤$t$，它的输出$y_t$成为下一步的输入$x_{t+1}\backsim y_t$。

GraphRNN的训练过程

GraphRNN的训练过程使用了已有的Graph数据。

• 对于节点级别的RNN，以SOS作为初始的输入$x_1$，同时也是RNN的初始隐藏值$s_0$，产生第一个输出$y_1$。
• 由于图的第一个节点没有边，所以可以直接产生第一个节点，然后以此节点开始后续，生成第二个节点。
• 然后，开始第一个边级别的RNN的生成，直到生成第二个节点的所有边。
• 用第二个节点生成的所有边$y_1$和第二个节点的隐藏状态$s_1$共同作为输入，再次进入节点级别的RNN，生成第三个节点。
• 重复上述过程，直到节点级别输出的$y$是EOS，结束。

上面过程的一个演示如下图：
其中，需要注意的地方有两点：

1. 在边级别RNN里面的输入也是从SOS开始，而且每次并不是使用$y_t$作为下一轮的输入，而是使用真实训练图里的边。这是课程里所说的"Teacher forcing"的训练方法。这一点和通常的RNN训练不太一样；
2. 新的节点的产生是使用上一轮的所有的边形成的向量，但是这里怎么把向量变成同一长度，课程里没有讲，需要看论文。

训练过程会对每个边计算交叉熵损失函数，并用这个损失值反向传播更新模型的参数。

GraphRNN的推断过程

在通过上面的训练得到了模型后，就可以遵循几乎一样的过程来生成新的图了。但这里面有一个问题，就是用SOS开始图生成过程的话，由于模型里面的参数都是确定了，那么使用确定的SOS作为初始的输入，节点和边级别RNN得到的计算结果就是确定的。那么如果按照0.5作为阈值来确定是否创建边，每次得到的图就完全一样了。

所以在实际生成的过程中，并不会使用模型的输出概率来直接创建边，而是按照边级别RNN的每次输出值的概率掷骰子得到0和1来确定是否要建边。然后再把是否有边的结果送给下一步的RNN来继续。

用这个方法就带来了随机性，从而保证了每次生成的图都不会完全一样。

GraphRNN的计算复杂性

对于GraphRNN算法，还有一个计算复杂度的问题，其实是空间复杂度的问题。即在推断过程，如果要每个新的节点都要和之前所有节点计算是否有边的概率。这么做的话就等于是几乎完全生成$N\times N$的邻接矩阵。因此在这里，GraphRNN算法采用了一个trick来降低这个计算复杂度的问题。

基本思想是采用BFS的方法来对节点进行排序，从而让后续节点保证不会和2步之前的节点之间有边。这样在后续节点的边生成过程，就不再需要计算和2步之前的节点是否有边了。通过这种方法，就把生成$N\times N$邻接矩阵的任务，变成了生成3条对角线矩阵的问题。如下图所示：

结果评估：
对于图生成，如何评估是一个难题。这个论文给了两种评估方法：

1. 人工视觉评估，课程里展示了这个方法的结果。这种方法一般都使用人造的数据来进行比对，图的规模也不会很大。
2. 图特征的统计结果比对。这个方法可以比较超过人工识别的规模的图。

图生成的应用

课程里介绍了图生成的另外一个应用：受限受控的分子图生成。这里就不再笔记分析了。有兴趣的去看他们论文就好了。
Graph Convolutional Policy Network for Goal-Directed Molecular Graph Generation

[第十课笔记结束]