RNN、LSTM、GRU、DeepRNN和BiLSTM
RNN(Recurrent Neural Network)
H t = ϕ ( X t W x h + H t − 1 W h h + b h ) (1) \boldsymbol H_t=\phi(X_tW_{xh}+H_{t-1}W_{hh}+b_h) \tag 1 Ht=ϕ(XtWxh+Ht−1Whh+bh)(1)
O U T P U T t = H t W h q + b q (2) \boldsymbol {OUTPUT_t}=\boldsymbol H_t \boldsymbol W_{hq}+\boldsymbol b_q \tag 2 OUTPUTt=HtWhq+bq(2)
其中, X t ∈ R n × d \boldsymbol X_t \in R^{n \times d} Xt∈Rn×d是时间步 t t t的小批量输入, H t ∈ R n × h H_t \in R^{n \times h} Ht∈Rn×h是该时间步的隐藏变量, n n n为batch_size, d d d为一个词编码后的向量维度, h h h为隐藏神经元数量, W x h ∈ R d × h \boldsymbol W_{xh} \in R^{d \times h} Wxh∈Rd×h, W h h ∈ R h × h \boldsymbol W_{hh} \in R^{h \times h} Whh∈Rh×h, b h ∈ R 1 × h \boldsymbol b_h \in R^{1 \times h} bh∈R1×h, ϕ \phi ϕ为非线性激活函数。因为引入了 H t − 1 W h h H_{t-1}W_{hh} Ht−1Whh, H t H_t Ht可以捕捉截至当前步的序列历史信息。在时间步 t t t,输出层的输出为 O t O_t Ot, W h q ∈ R h × q W_{hq} \in R^{h \times q} Whq∈Rh×q, b q ∈ R 1 × q b_q \in R^{1 \times q} bq∈R1×q。 q q q为输出维度大小。公式中含有$\boldsymbol W_{xh},\boldsymbol W_{hh}, \boldsymbol b_h,\boldsymbol W_{hq},\boldsymbol b_q$5个权重矩阵参数需要学习得到。
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
# num_inputs: d
# num_hiddens: h, 隐藏单元的个数是超参数
# num_outputs: q
def get_params():
def _one(shape):
param = torch.zeros(shape, device=device, dtype=torch.float32)
nn.init.normal_(param, 0, 0.01)
return torch.nn.Parameter(param)
# 隐藏层参数
W_xh = _one((num_inputs, num_hiddens))
W_hh = _one((num_hiddens, num_hiddens))
b_h = torch.nn.Parameter(torch.zeros(num_hiddens, device=device))
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device))
return (W_xh, W_hh, b_h, W_hq, b_q)
RNN使用循环来完成前向计算:
def rnn(inputs, state, params):
# inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵
W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
H = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(H, W_hh) + b_h)
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)
另外,神经网络需要初始化一个隐藏状态变量 H 0 H_0 H0,隐藏状态初始化:
def init_rnn_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )
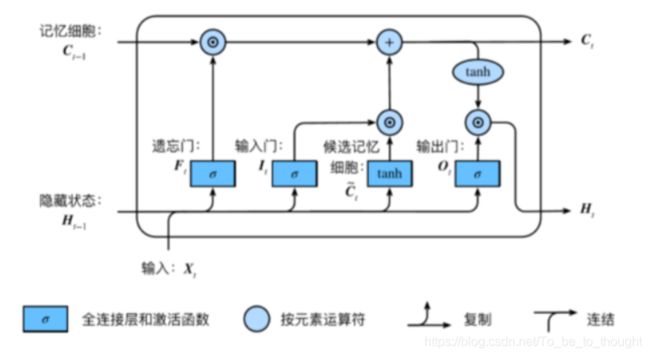
LSTM
I t = σ ( X t W x i + H t − 1 W h i + b i ) (3) I_t=\sigma(\boldsymbol {X_t W_{xi}}+\boldsymbol {H_{t-1} W_{hi}}+\boldsymbol b_i) \tag 3 It=σ(XtWxi+Ht−1Whi+bi)(3)
F t = σ ( X t W x f + H t − 1 W h f + b f ) (4) F_t=\sigma(\boldsymbol{ X_t W_{xf}}+H_{t-1}W_{hf}+\boldsymbol b_{f}) \tag 4 Ft=σ(XtWxf+Ht−1Whf+bf)(4)
O t = σ ( X t W x o + H t − 1 W h o + b o ) (5) O_t = \sigma(\boldsymbol {X_t W_{xo}} + \boldsymbol {H_{t-1}W_{ho} }+ \boldsymbol b_{o}) \tag 5 Ot=σ(XtWxo+Ht−1Who+bo)(5)
C t ~ = t a n h ( X t W x c + H t − 1 W h c + b c ) (6) \boldsymbol{\widetilde{C_t}} = tanh(\boldsymbol {X_t W_{xc}} + \boldsymbol {H_{t-1} W_{hc}} +\boldsymbol b_{c}) \tag 6 Ct =tanh(XtWxc+Ht−1Whc+bc)(6)
C t = F t ⨂ C t − 1 + I t ⨂ C t ~ (7) \boldsymbol C_t = \boldsymbol F_t \bigotimes \boldsymbol C_{t-1}+\boldsymbol I_t \bigotimes \boldsymbol{\widetilde{C_t}} \tag 7 Ct=Ft⨂Ct−1+It⨂Ct (7)
H t = O t ⨂ t a n h ( C t ) (8) \boldsymbol H_t=\boldsymbol O_t \bigotimes tanh(\boldsymbol C_t) \tag 8 Ht=Ot⨂tanh(Ct)(8)
其中, X t ∈ R n × d \boldsymbol X_t \in R^{n \times d} Xt∈Rn×d是时间步 t t t的小批量输入, H t ∈ R n × h H_t \in R^{n \times h} Ht∈Rn×h是该时间步的隐藏变量, I t , F t , C t ~ , O t I_t,F_t,\boldsymbol{\widetilde{C_t}},O_t It,Ft,Ct ,Ot分别表示输入门、遗忘门、候选记忆细胞和输出门, σ \sigma σ表示sigmoid函数, ⨂ \bigotimes ⨂表示Hadmard积。 W x i ∈ R , W_{xi} \in R^{}, Wxi∈R,。每一个LSTM单元包含 W x i ∈ R d × h , W h i ∈ R h × h , b i ∈ R 1 × h \boldsymbol{W_{xi}} \in R^{d \times h},\boldsymbol {W_{hi}} \in R^{h \times h} ,b_i \in R^{1 \times h} Wxi∈Rd×h,Whi∈Rh×h,bi∈R1×h , W x f ∈ R d × h , W h f ∈ R h × h , b f ∈ R 1 × h W_{xf} \in R^{d \times h} ,W_{hf} \in R^{h \times h} ,b_{f} \in R^{1 \times h} Wxf∈Rd×h,Whf∈Rh×h,bf∈R1×h , W x o ∈ R d × h , W h o ∈ R h × h , b o ∈ R 1 × h W_{xo} \in R^{d \times h} ,W_{ho} \in R^{ h \times h} ,b_{o} \in R^{1 \times h} Wxo∈Rd×h,Who∈Rh×h,bo∈R1×h ,$W_{xc} \in R^{d \times h} , , ,W_{hc} \in R^{h \times h} ,b_{c} \in R^{1 \times h} , , ,W_{hq} \in R^{h \times q},b_q \in R^{1 \times q}$共14个权重矩阵参数需要学习。
输出计算为:
O U T P U T t = H t W h q + b q \boldsymbol {OUTPUT_t}=\boldsymbol H_t \boldsymbol W_{hq}+\boldsymbol b_q OUTPUTt=HtWhq+bq
代码如下:
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xi, W_hi, b_i = _three() # 输入门参数
W_xf, W_hf, b_f = _three() # 遗忘门参数
W_xo, W_ho, b_o = _three() # 输出门参数
W_xc, W_hc, b_c = _three() # 候选记忆细胞参数
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q])
另外,隐藏状态和记忆细胞都需要初始化状态:
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
构建的LSTM使用迭代的方式进行前向计算
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
C = F * C + I * C_tilda
H = O * C.tanh()
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H, C)
使用现成的LSTM:
num_hiddens=256
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
lr = 1e-2 # 注意调整学习率
lstm_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens)
model = d2l.RNNModel(lstm_layer, vocab_size)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)
GRU
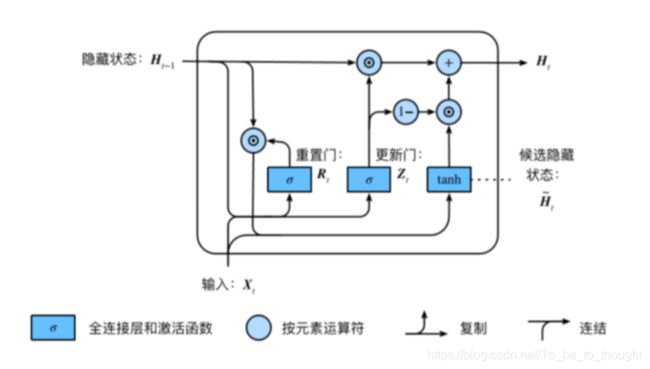
R t = σ ( X t W x r + H t − 1 W h r + b r ) (9) R_t=\sigma(X_tW_{xr}+H_{t-1}W_{hr}+b_r) \tag 9 Rt=σ(XtWxr+Ht−1Whr+br)(9)
Z t = σ ( X t W x z + H t − 1 W h z + b z ) (10) Z_t=\sigma(X_t W_{xz}+H_{t-1}W_{hz}+b_z) \tag {10} Zt=σ(XtWxz+Ht−1Whz+bz)(10)
H t ~ = t a n h ( X t W x h + ( R t ⨂ H t − 1 ) W h h + b h ) (11) \widetilde{H_t}=tanh(X_t W_{xh}+(R_t \bigotimes H_{t-1})W_{hh}+b_h) \tag{11} Ht =tanh(XtWxh+(Rt⨂Ht−1)Whh+bh)(11)
H t = Z t ⨂ H t − 1 + ( 1 − Z t ) ⨂ H t ~ (12) H_t = Z_t \bigotimes H_{t-1}+(1-Z_t)\bigotimes \widetilde{H_t} \tag{12} Ht=Zt⨂Ht−1+(1−Zt)⨂Ht (12)
其中, X t ∈ R n × d \boldsymbol X_t \in R^{n \times d} Xt∈Rn×d是时间步 t t t的小批量输入, H t ∈ R n × h H_t \in R^{n \times h} Ht∈Rn×h是该时间步的隐藏变量,没每个GRU单元包括 W x r ∈ R d × h , W h r ∈ R h × h , b r ∈ R 1 × h W_{xr} \in R^{d \times h},W_{hr} \in R^{h \times h},b_r \in R^{1 \times h} Wxr∈Rd×h,Whr∈Rh×h,br∈R1×h, W x z ∈ R d × h , W h z ∈ R h × h , b z ∈ R 1 × h W_{xz} \in R^{d \times h},W_{hz} \in R^{h \times h},b_z \in R^{1 \times h} Wxz∈Rd×h,Whz∈Rh×h,bz∈R1×h, W x h ∈ R d × h , W h h ∈ R h × h , b h ∈ R 1 × h W_{xh} \in R^{d \times h},W_{hh} \in R^{h \times h},b_h \in R^{1 \times h} Wxh∈Rd×h,Whh∈Rh×h,bh∈R1×h, W h q ∈ R h × q , b q ∈ R 1 × q W_{hq} \in R^{h \times q},b_q \in R^{1 \times q} Whq∈Rh×q,bq∈R1×q共11个权重矩阵参数需要学习。
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32) #正态分布
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xz, W_hz, b_z = _three() # 更新门参数
W_xr, W_hr, b_r = _three() # 重置门参数
W_xh, W_hh, b_h = _three() # 候选隐藏状态参数
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q])
t t t时间步的输出计算:
O U T P U T t = H t W h q + b q \boldsymbol {OUTPUT_t}=\boldsymbol H_t \boldsymbol W_{hq}+\boldsymbol b_q OUTPUTt=HtWhq+bq
GRU单元只需要初始化隐藏状态矩阵:
def init_gru_state(batch_size, num_hiddens, device): #隐藏状态初始化
return (torch.zeros((batch_size, num_hiddens), device=device), )
GRU的前向计算迭代方式实现:
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid(torch.matmul(X, W_xz) + torch.matmul(H, W_hz) + b_z)
R = torch.sigmoid(torch.matmul(X, W_xr) + torch.matmul(H, W_hr) + b_r)
H_tilda = torch.tanh(torch.matmul(X, W_xh) + R * torch.matmul(H, W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)
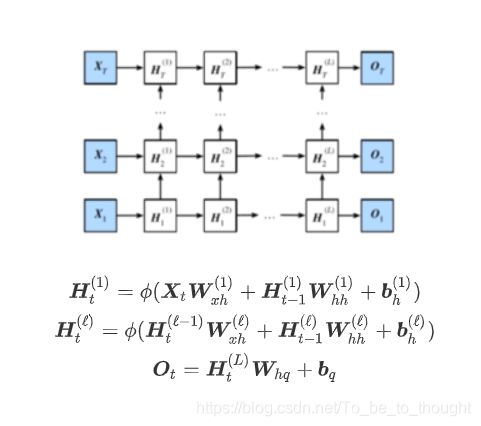
深度循环神经网络
代码:
num_hiddens=256
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
lr = 1e-2 # 注意调整学习率
gru_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens,num_layers=2)
model = d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)
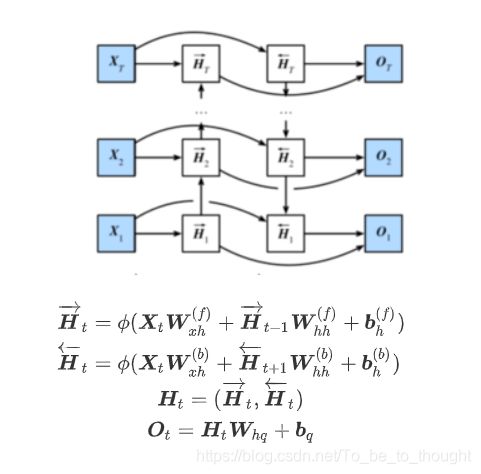
BiLSTM
代码:
num_hiddens=128
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e-2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
lr = 1e-2 # 注意调整学习率
gru_layer = nn.GRU(input_size=vocab_size, hidden_size=num_hiddens,bidirectional=True)
model = d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
corpus_indices, idx_to_char, char_to_idx,
num_epochs, num_steps, lr, clipping_theta,
batch_size, pred_period, pred_len, prefixes)