前言需求
今天我们学习的是普里姆算法,我们还是从一个场景里引入看看
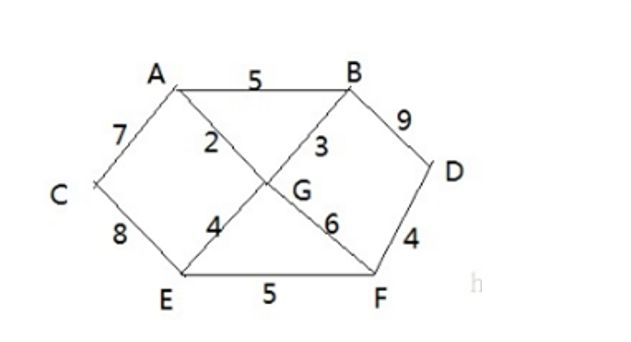
有7个村庄(A, B, C, D, E, F, G) ,现在需要修路把7个村庄连通
1.各个村庄的距离用边线表示(权) ,比如 A – B 距离 5公里
2.问如何修路保证各个村庄都能连通,并且总的修建公路总里程最短?
我们的思路就是尽可能的选择少的路线,并且每条路线最小,保证总里程数最少
一、什么是普里姆算法
普利姆(Prim)算法求:最小生成树就是在包含n个顶点的连通图中,找出只有(n-1)条边包含所有n个顶点的连通子图,也就是所谓的极小连通子图
二、通过示例认识普里姆算法
其实修路的问题本质就是最小生成树的问题
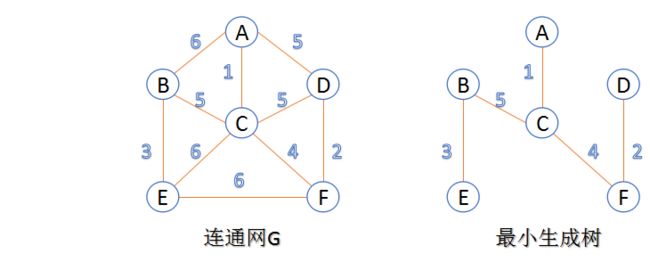
先介绍一下最小生成树(Minimum Cost Spanning Tree),简称MST
那么什么是最小生成树呢?其实就是给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小。这叫最小生成树
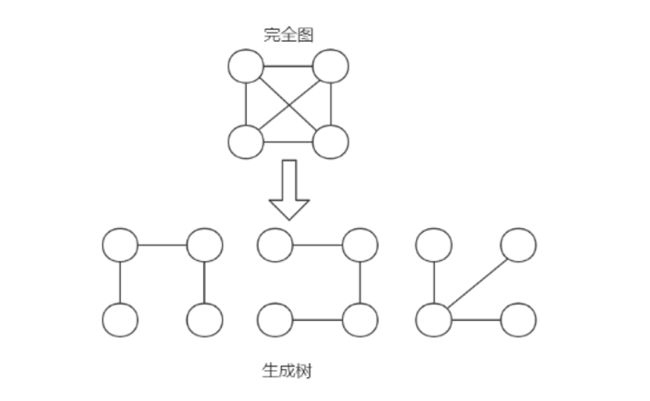
那么最小生成树有什么特点呢?
1.若有N个顶点,一定要至少有N-1条边
2.图要包含全部顶点
3.N-1条边要都在图中
那么求最小生成树的算法主要有普里姆算法和克鲁斯卡尔算法
普里姆算法思路分析
1.设G=(V,E)是连通网,T=(U,D)是最小生成树,V,U是顶点集合,E,D是边的集合
2.若从顶点u开始构造最小生成树,则从集合V中取出顶点u放入集合U中,标记顶点v的visited[u]=1
3.若集合U中顶点ui与集合V-U中的顶点vj之间存在边,则寻找这些边中权值最小的边,但不能构成回路。
将顶点vj加入集合U中,将边(ui,vj)加入集合D中,标记visited[vj]=1
4.重复步骤②,直到U与V相等,即所有顶点都被标记为访问过,此时D中有n-1条边
普里姆算法图解思路分析
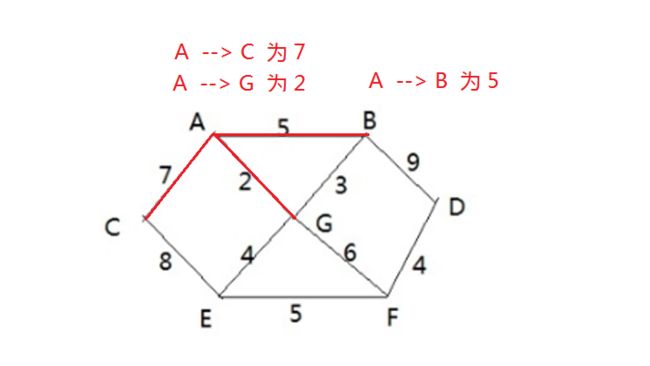
1.假如从A顶点开始处理,将A放入集合中,并可连接到其他顶点有C、G、B
2.此时这三条边的最小权重值是A-G 为2,于是我们G放入集合中,《A,G》
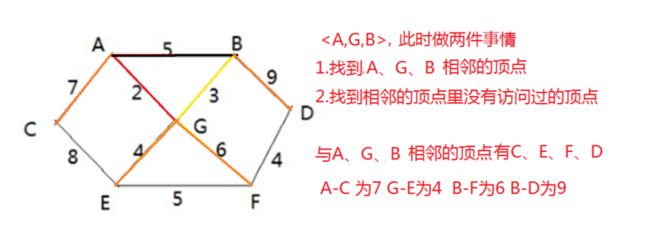
3.此时这五条边的最小权重值是B-B 为3,于是我们B放入集合中,《A,G,B》
4.此时这四条边的最小权重值是G-E 为4,于是我们E放入集合中,《A,G,B,E》
此时这五条边的最小权重值是E-F 为5,以此类推加入到集合中....
最后的集合结果应该是
普里姆代码思路分析
1.我们需要一个存放顶点的char数组,以及顶点的边数
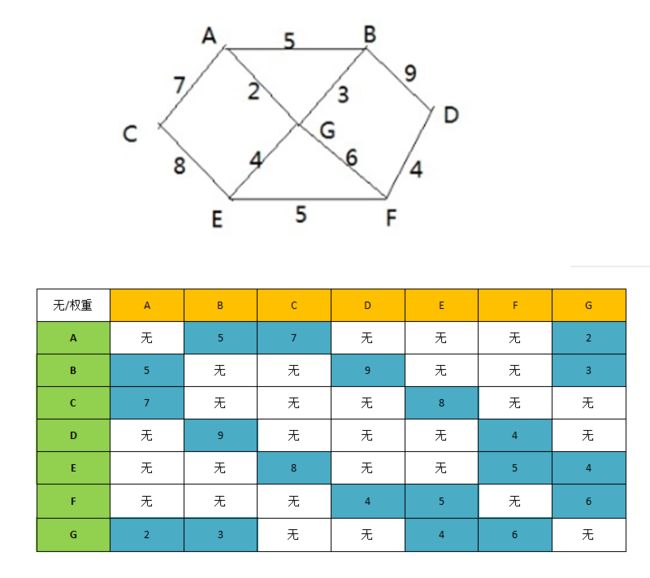
2.我们需要使用邻接矩阵来表示顶点之间的连接情况与权重值
3.我们需要生成minTree树
4.我们需要创建图
普里姆算法代码实践
1.使用邻接矩阵来表示图所之间连接关系与权重值
//使用邻接矩阵描述权重值表示0 代表无
int[][] weight = new int[][]{
{0,5,7,0,0,0,2},
{5,0,0,9,0,0,3},
{7,0,0,0,8,0,0},
{0,9,0,0,0,4,0},
{0,0,8,0,0,5,4},
{0,0,0,4,5,0,6},
{2,3,0,0,4,6,0}
}; 2.需要一个存放顶点的char数组,以及顶点的边数
//char[] 数组存放顶点个数
char[] data = new char[]{'A','B','C','D','E','F','G'};
int verxs = data.length;3.创建图对象
class MGraph{
int verxs;//表示图的节点数
char[] data;//存放结点数据
int[][] weight;//存放边
public MGraph(int verxs) {
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}4.我们需要将创建的这些值与数组、赋值给到图对象,并创建输出图的方法
class MinTree{
//创建图的邻接矩阵
public void createGraph(MGraph graph,int verxs,char[] data,int[][] weight){
for ( int i = 0 ; i接下来我们使用demo 完成图的创建与输出
public static void main(String[] args) {
//char[] 数组存放顶点个数
char[] data = new char[]{'A','B','C','D','E','F','G'};
//顶点之间的边
int verxs = data.length;
//使用邻接矩阵描述权重值表示0 代表无
int[][] weight = new int[][]{
{0,5,7,0,0,0,2},
{5,0,0,9,0,0,3},
{7,0,0,0,8,0,0},
{0,9,0,0,0,4,0},
{0,0,8,0,0,5,4},
{0,0,0,4,5,0,6},
{2,3,0,0,4,6,0}
};
MGraph graph = new MGraph(verxs);
MinTree minTree = new MinTree();
minTree.createGraph(graph,verxs,data,weight);
minTree.showGraph(graph);
}
根据普里姆算法思路编写算法代码
1.我们的思路是先找到一个顶点开始,不断找相邻顶点,比如说A开始
找相邻顶点的条件是:A已访问,其他顶点为未访问
2.判断A-其他顶点的weight,是否是最小的
为了方便找到最小的,我们这里使用一个很大的数,来代替刚刚的:0
public void prim(MGraph graph,int v){
//使用数组标注节点是否被访问过
int[] visited = new int[graph.verxs];
for ( int i=0; i 权值:" + minWeight);
visited[h2] = 1;
minWeight = 10000;
}
} 即将上图所至的0 --> 10000
public static void main(String[] args) {
//char[] 数组存放顶点个数
char[] data = new char[]{'A','B','C','D','E','F','G'};
//顶点之间的边
int verxs = data.length;
//使用邻接矩阵描述权重值表示0 代表无
int[][] weight = new int[][]{
{10000,5,7,10000,10000,10000,2},
{5,10000,10000,9,10000,10000,3},
{7,10000,10000,10000,8,10000,10000},
{10000,9,10000,10000,10000,4,10000},
{10000,10000,8,10000,10000,5,4},
{10000,10000,10000,4,5,10000,6},
{2,3,10000,10000,4,6,10000}
};
MGraph graph = new MGraph(verxs);
MinTree minTree = new MinTree();
minTree.createGraph(graph,verxs,data,weight);
minTree.showGraph(graph);
minTree.prim(graph,0);
}
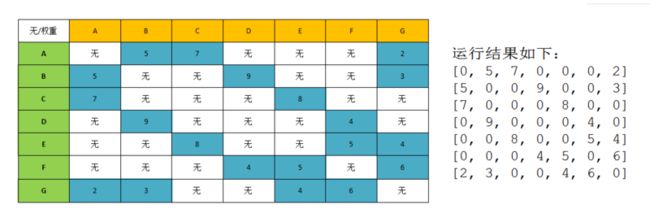
运行结果如下:
边 权值:2
边 权值:3
边 权值:4
边 权值:5
边 权值:4
边 权值:7 参考资料
- 尚硅谷:数据结构与算法(韩顺平老师):普里姆算法