一文搞懂卷积网络之一（【动态图】从LeNet到GoogLeNet）

闲聊

前面的“一文”系列项目，介绍了从用python手写回归模型，到用各种数据增强方法给CV模型涨点，再到用GAN“以优乱真”。这也是兄弟在Deep Learning海洋中的冲浪轨迹。本想做个“乘风破浪的调参侠”，结果，发现多数情况都是冲浪板儿飞得比人高。划水的时候我就反思这是肿么回事。喝过大口大口的海水后我发现自己的招式里有一个颇大的漏洞，就是经典模型掌握的不够清楚。跟着老师学CV、打识虫比赛的时候对模型太拿来主义了。我基本就是按着那些经典模型名头的大小和出产年份（和选茅台标准正相反）进行选美，然后看也不看就当做检测模型的backbone用了，再然后就用lr衰减、L2正则化项、数据增强（以及剪枝、蒸馏、多模型融合）等炼丹的奇技淫巧去给模型涨点了，恰恰忽略了最中正淳厚“经典模型”功夫。这里权当补课了。

一、卷积网络的前世今生

刚刚理解并跑过第一个一层全连接层的回归模型的时候，我兴奋的以为自己已经掌握了机器学习的“宇宙真理”，从此，任何信息包括图片的像素信息只要输入神经网络，就能映射出想要的回归或分类结果了。后来才发现，动辄像素数以万计的图片数据用全连接层组成复杂网络的话，参数规模也是“宇宙级别”的，在地球上使用这么多的算力目前是不科学的。而且，将具有二维空间特征的信息强行拉成一维，丢失了相对位置信息也并不利于模型高效的学习。而卷积神经网络具有“参数共享”、“重叠池化”和“平移不变”的特征，大大减少了参数规模，能够层次化得提取像素的二维空间特征并且比全连接层组成的网络具有更强的位置鲁棒性。

日本学者福岛邦彦于1980年提出了Neocognitron模型，有了类似卷积和池化的概念，奠定了卷积神经网络的基础。1989年Yann LeCun对权重进行初始化后使用随机梯度下降法训练网络，并首次使用“卷积”命名这种神经网络。BP（反向传播）的使用对于多层卷积神经网络的训练至关重要。至此，卷积神经网络成型。1998年Yann LeCun提出的LeNet-5在手写数字识别任务上取得了很好的效果,LeNet-5的结构也成为了现代卷积神经网络的基础。此后一段时间，由于算力和数据的限制，深度学习技术发展遭遇了瓶颈。而同时期SVM、HMM等其他机器学习算法的性能更加出彩。直到2012年，Hinton和他的学生Alex Krizhevsky设计的AlexNet获得了当年ImageNet比赛的冠军，深度学习再次回到了赛道的前沿并领跑至今。过后VGG、GoogLeNet等更深、更复杂的网络相继提出，进一步提升了深度卷积网络的性能。但是，当网络的深度达到二十层左右后，再增加更多层的网络会导致梯度消失，无法进一步提升性能，即出现了网络退化现象。2015年何恺明等4位学者提出了利用残差块的跨层连接缓解增加网络深度导致的梯度消失问题，从而使网络的深度突破了此前二十几层的限制达到了成百上千层，更进一步的提升了深度网络的性能。此后的DenseNet则通过使用更加密集的跨层连接进一步提升的性能。近些年来由于ResNet的简单易用效果好，各种变体层出不穷。引入并改良了当红的注意力机制的ResNetSt则号称ResNet的最强变体。近期，也有学者开始探索让卷积网络让卷积网络提取图片中物体的三维特征，推进模型对物体从感知到理解的进程。

卷积计算

卷积是数学分析中的一种积分变化的方法，在图像处理中采用的是卷积的离散形式。这里需要说明的是，在卷积神经网络中，卷积层的实现方式实际上是数学中定义的互相关 （cross-correlation）运算，与数学分析中的卷积定义有所不同，这里跟其他框架和卷积神经网络的教程保持一致，都使用互相关运算作为卷积的定义，具体的计算过程如 图1 所示。

图1：卷积计算过程

---

说明：

卷积核（kernel）也被叫做滤波器（filter），假设卷积核的高和宽分别为$k_h$和$k_w$，则将称为$k_h\times k_w$卷积，比如$3\times 5$卷积，就是指卷积核的高为3, 宽为5。

---

• 如图1（a）所示：左边的图大小是$3\times 3$，表示输入数据是一个维度为$3\times 3$的二维数组；中间的图大小是$2\times 2$，表示一个维度为$2\times 2$的二维数组，我们将这个二维数组称为卷积核。先将卷积核的左上角与输入数据的左上角（即：输入数据的(0, 0)位置）对齐，把卷积核的每个元素跟其位置对应的输入数据中的元素相乘，再把所有乘积相加，得到卷积输出的第一个结果

$$0\times 1+1\times 2+2\times 4+3\times 5=25(a)$$

• 如图1（b）所示：将卷积核向右滑动，让卷积核左上角与输入数据中的(0,1)位置对齐，同样将卷积核的每个元素跟其位置对应的输入数据中的元素相乘，再把这4个乘积相加，得到卷积输出的第二个结果，

$$0\times 2+1\times 3+2\times 5+3\times 6=31(b)$$

• 如图1（c）所示：将卷积核向下滑动，让卷积核左上角与输入数据中的(1, 0)位置对齐，可以计算得到卷积输出的第三个结果，

$$0\times 4+1\times 5+2\times 7+3\times 8=43(c)$$

• 如图1（d）所示：将卷积核向右滑动，让卷积核左上角与输入数据中的(1, 1)位置对齐，可以计算得到卷积输出的第四个结果，

$$0\times 5+1\times 6+2\times 8+3\times 9=49(d)$$

卷积核的计算过程可以用下面的数学公式表示，其中 $a$ 代表输入图片， $b$ 代表输出特征图，$w$ 是卷积核参数，它们都是二维数组，$\sum u,v$ 表示对卷积核参数进行遍历并求和。

$$b[i,j]=\sum _{u,v}a[i+u,j+v]\cdot w[u,v]$$

举例说明，假如上图中卷积核大小是$2\times 2$，则$u$可以取0和1，$v$也可以取0和1，也就是说：
$$b[i,j]=a[i+0,j+0]\cdot w[0,0]+a[i+0,j+1]\cdot w[0,1]+a[i+1,j+0]\cdot w[1,0]+a[i+1,j+1]\cdot w[1,1]$$

读者可以自行验证，当$[i,j]$取不同值时，根据此公式计算的结果与上图中的例子是否一致。

在卷积神经网络中，一个卷积算子除了上面描述的卷积过程之外，还包括加上偏置项的操作。例如假设偏置为1，则上面卷积计算的结果为：

$$0\times 1+1\times 2+2\times 4+3\times 5+1=26$$
$$0\times 2+1\times 3+2\times 5+3\times 6+1=32$$
$$0\times 4+1\times 5+2\times 7+3\times 8+1=44$$
$$0\times 5+1\times 6+2\times 8+3\times 9+1=50$$

---

上面这段“卷积计算”的介绍转自《百度架构师手把手教深度学习》课程的“卷积神经网络基础”章节。我觉得这是我学习过的最清晰直观的卷积计算的描述了，就没有重新画轮子。

下面我们上手经典模型。

二、动手卷积神经网络的经典模型

我们逐一用 Paddle 的动态图模式实现LeNet、AlexNet、VGG和GoogLeNet，以帮助各位同学更加直观的（相对于静态图模型）了解模型结构。数据集采用从Caltech数据集中抽取16类的mini版本。

先解压数据集并导入需要的包。

# # 解压数据集，首次执行后注释掉
# !unzip -d /home/aistudio/work /home/aistudio/data/data22612/Images.zip
# !mkdir /home/aistudio/work/labels
# !cp /home/aistudio/data/data22612/Train.txt /home/aistudio/work/labels
# !cp /home/aistudio/data/data22612/Eval.txt /home/aistudio/work/labels
# !cp /home/aistudio/data/data22612/Test.txt /home/aistudio/work/labels

# 导入需要的包
import paddle
import paddle.fluid as fluid
import numpy as np
from paddle.fluid.dygraph import Conv2D, Pool2D, Linear, Dropout, BatchNorm

from train import train

epoch_num = 60
batch_size = 32

1.LetNet

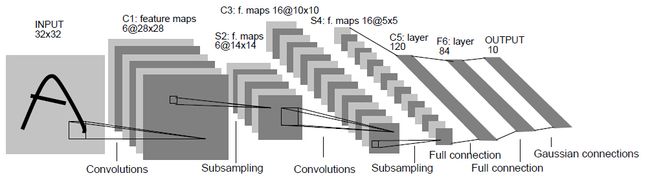
LeNet大体上由提取特征的三个卷积层和两个分类的全连接层组成。(图片来自网络)

• 卷积层和全连接层采用Sigmoid激活函数。

• 三个全连接层之间插入了两个池化层来缩小特征图，以使后面的卷积层提取更大尺度的特征。池化层采用最大池化方式。

• 原版的输出层由欧式径向基函数单元组成。此处用softmax输出单元。输出数量为分类的类别数量。

• LeNet原本是设计用来分类输入尺寸为32×32的手写数字图片的，此处用来分类输入为224×224的Caltech数据集图片。（Paddle1.7版本后要求显示声明各个网络层的输入维度，所以在将二维的卷积层输出的特征图拉伸为一维时需要计算尺寸）

#LeNet网络定义
class LeNet(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(LeNet, self).__init__(name_scope)
        name_scope = self.full_name()
        self.conv1 = Conv2D(num_channels=3, num_filters=6, filter_size=5, act='sigmoid')
        self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
        self.conv2 = Conv2D(num_channels=6, num_filters=16, filter_size=5, act='sigmoid')
        self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
        self.conv3 = Conv2D(num_channels=16, num_filters=120, filter_size=4, act='sigmoid')
        
        #conv3层输出通道数为120、特征图尺寸为50×50.所以下面fc1层的输入维度为120×50×50
        self.fc1 = Linear(input_dim=120 * 50 * 50, output_dim=84, act='sigmoid')
        self.fc2 = Linear(input_dim=84, output_dim=num_classes)
    
    # 前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.pool1(x)
        x = self.conv2(x)
        x = self.pool2(x)
        x = self.conv3(x)
        x = fluid.layers.reshape(x, [-1, 120 * 50 * 50])# 将二维的卷积层输出的特征图拉伸为同等大小的1维
        x = self.fc1(x)
        x = self.fc2(x)
        return x

#训练过程
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = LeNet("LeNet", num_classes=16)
    train(epoch_num, batch_size, model)

2.AlexNet

得益于硬件的发展（GPU的使用等）和各种算法的改进，在2012的 ImageNet 图像分类竞赛中，AlexeNet 以远超第二名的成绩夺冠，使得深度学习重回历史舞台，具有重大历史意义。AlexNet主要由5层卷积层和3层全连接层组成。(图片来自网络)

• 采用ReLU激活函数（The Rectified Linear Unit修正线性单元）代替了LeNet中的Sigmoid激活函数。ReLU激活函数的单侧抑制特性，使得神经网络中的神经元具有了稀疏激活性，可以在 BP 的时候将梯度很好地传到较前面的网络。

• 在卷积层后使用尺寸（为3）大于步长（为2）的重叠池化降低网络的过拟合。

• 在全连接层之间采用DropOut层随机抛掉部分神经元以降低网络的过拟合。

• 开始使用GPU加速训练、使用mini batch进行带动量的随机梯度下降、使用数据增强（GPU加速、mini batch划分现在已普遍使用。在本项目中为了比较各个模型的性能，均未使用数据增强）

class AlexNet(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(AlexNet, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 96, 11, stride=4, padding=2, act='relu')
        self.pool1 = Pool2D(pool_size=3, pool_stride=2, pool_type='max')
        self.conv2 = Conv2D(96, 256, 5, stride=1, padding=2, act='relu')
        self.pool2 = Pool2D(pool_size=3, pool_stride=2, pool_type='max')
        self.conv3 = Conv2D(256, 384, 3, stride=1, padding=1, act='relu')
        self.conv4 = Conv2D(384, 384, 3, stride=1, padding=1, act='relu')
        self.conv5 = Conv2D(384, 256, 3, stride=1, padding=1, act='relu')
        self.pool5 = Pool2D(pool_size=3, pool_stride=2, pool_type='max')
        self.fc1 = Linear(256 * 6 * 6, 4096, act='relu')
        self.drop_out1 = Dropout(p=0.5)
        self.fc2 = Linear(4096, 4096, act='relu')
        self.drop_out2 = Dropout(p=0.5)
        self.fc3 = Linear(4096, num_classes, act='relu')

    def forward(self, x):
        x = self.conv1(x)
        x = self.pool1(x)
        x = self.conv2(x)
        x = self.pool2(x)
        x = self.conv3(x)
        x = self.conv4(x)
        x = self.conv5(x)
        x = self.pool5(x)

        x = fluid.layers.reshape(x, [-1, 256 * 6 * 6])
        x = self.fc1(x)
        x = self.drop_out1(x)
        x = self.fc2(x)
        x = self.drop_out2(x)
        x = self.fc3(x)

        return x

#训练过程
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = AlexNet("AlexNet", num_classes=16)
    train(epoch_num, batch_size, model)

3.VGG

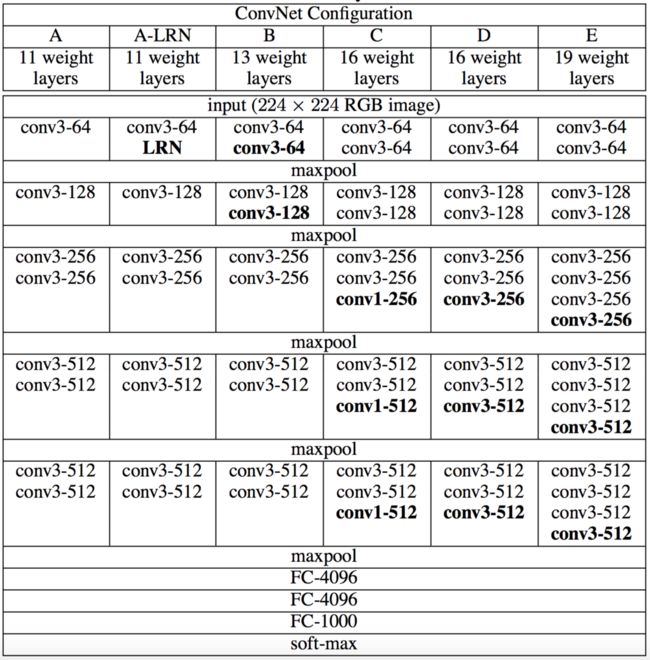
“VGG”代表了牛津大学的Oxford Visual Geometry Group。VGG模型采用模块化的方式将网络堆叠到了19层以增强性能。(图片来自网络)

• VGG网络的研究者证明了小尺寸卷积核（3x3 ）的深层网络要优于大尺寸卷积核的浅层网络，所以全部采用3×3的卷积核代替了其他的大尺寸卷积核。

• 由于网络深度较深，因此网络权重的初始化很重要，可以通过 Xavier均匀初始化，否则可能会阻碍学习。

• VGG有13、16、19等多种尺度规格。训练VGG16、VGG19这样的深层网络时，可以逐层训练。先训练VGG13，然后冻结前面的层对后面的层进行微调。

class VGG(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1, layer=13):
        super(VGG, self).__init__(name_scope)
        name_scope = self.full_name()

        self.layer = layer

        self.pool = Pool2D(pool_size=2, pool_stride=2)
        self.drop_out = Dropout(p=0.5)

        self.conv1 = Conv2D(3, 64, 3, padding=1, act='relu')
        self.conv2 = Conv2D(64, 64, 3, padding=1, act='relu')

        self.conv3 = Conv2D(64, 128, 3, padding=1, act='relu')
        self.conv4 = Conv2D(128, 128, 3, padding=1, act='relu')

        self.conv5 = Conv2D(128, 256, 3, padding=1, act='relu')
        self.conv6 = Conv2D(256, 256, 3, padding=1, act='relu')
        self.conv7 = Conv2D(256, 256, 3, padding=1, act='relu')
        self.conv8 = Conv2D(256, 256, 3, padding=1, act='relu')

        self.conv9 = Conv2D(256, 512, 3, padding=1, act='relu')
        self.conv10 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv11 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv12 = Conv2D(512, 512, 3, padding=1, act='relu')

        self.conv13 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv14 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv15 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv16 = Conv2D(512, 512, 3, padding=1, act='relu')

        self.fc1 = Linear(input_dim=512 * 7 * 7, output_dim=4096, act='relu')
        self.fc2 = Linear(input_dim=4096, output_dim=4096, act='relu')
        self.fc3 = Linear(input_dim=4096, output_dim=num_classes)

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.pool(x)

        x = self.conv3(x)
        x = self.conv4(x)
        x = self.pool(x)

        x = self.conv5(x)
        x = self.conv6(x)
        if self.layer >= 16:
            x = self.conv7(x)
        if self.layer >= 19:
            x = self.conv8(x)
        x = self.pool(x)

        x = self.conv9(x)
        x = self.conv10(x)
        if self.layer >= 16:
            x = self.conv11(x)
        if self.layer >= 19:
            x = self.conv12(x)
        x = self.pool(x)

        x = self.conv13(x)
        x = self.conv14(x)
        if self.layer >= 16:
            x = self.conv15(x)
        if self.layer >= 19:
            x = self.conv16(x)
        x = self.pool(x)
 
        x = fluid.layers.reshape(x, [-1, 512 * 7 * 7])
        x = self.fc1(x)
        x = self.drop_out(x)
        x = self.fc2(x)
        x = self.drop_out(x)
        x = self.fc3(x)
        return x

#训练过程
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = VGG("VGG", num_classes=16)
    train(epoch_num, batch_size, model)

4.GoogLeNet

GoogLeNet获得了2014年ILSVRC竞赛的第一名，其不但提高了性能而且比较前的VGG、AlexNet降低了参数规模。

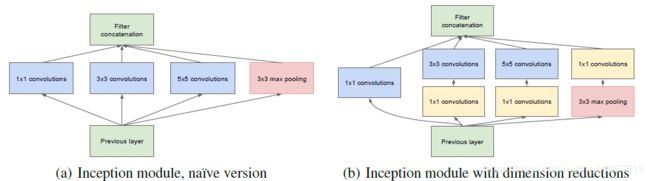
这是通过一种称为Inception的模块实现的。该模块的v1（最初）版本将1×1、3×3、5×5的卷积层和3×3的最大池化层拼接在一起，使其能够在一层网络中提取不同视野范围的特征。(图片来自网络)

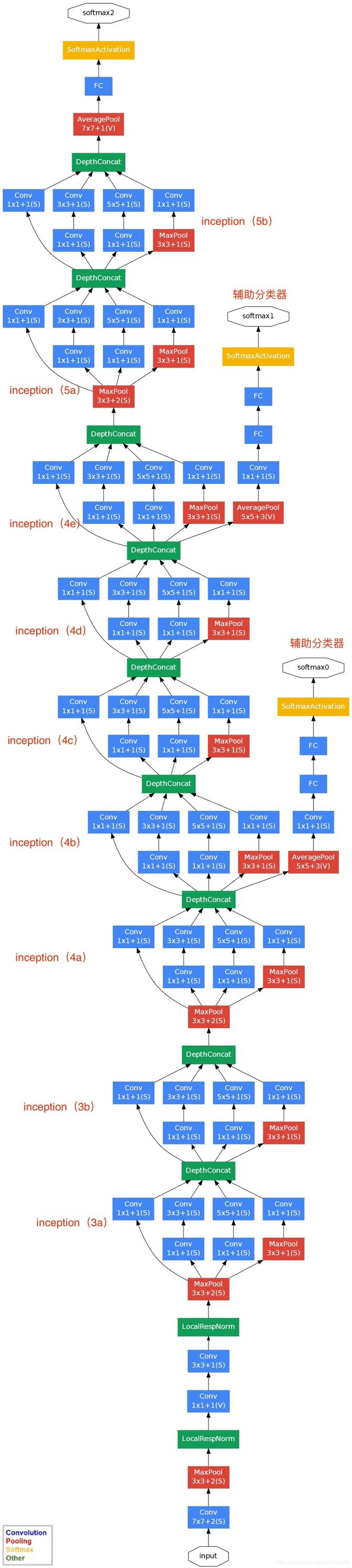
GoogLeNet的Inception v1版本的全部网络结构如下：(图片来自网络)

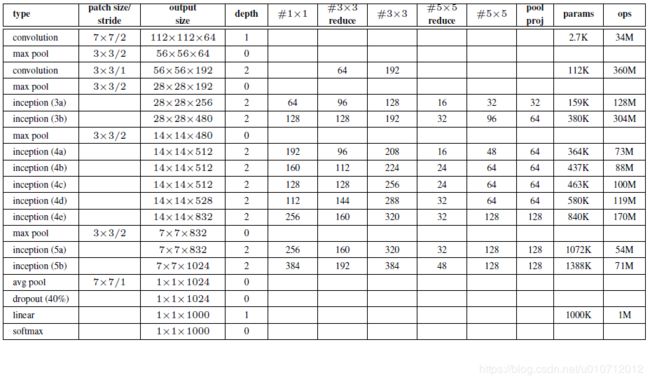
各层参数信息如下表：(图片来自网络)

• 使用1×1的卷积层进行降维大大减少了参数数量而又不影响性能。(图片来自网络)
  
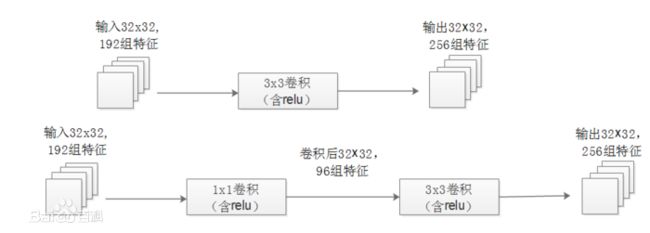
• 在卷积层和全连接层之间插入一个全局平均池化层，以减少模型参数。以前的模型是将二维的卷积层输出的特征图直接拉成一维的全连接层输入。
• 使用辅助分类器缓解梯度消失的问题。如前面的GoogLeNet结构全图所示：两个辅助分类器分别在Inception（4a）和Inception（4d）之后。辅助分类器在训练期间占损失函数权重的30%，在推理时不使用。（本项目中为了更清晰的展示GoogLeNet的结构没有加入辅助分类器，而且在后来的深度卷积网络的演化中也未再被使用。）

# 定义Inception块（Inception v1）
class Inception(fluid.dygraph.Layer):
    def __init__(self, name_scope, c1, c2, c3, c4):
        super(Inception, self).__init__(name_scope)
        name_scope = self.full_name()

        self.p1_1 = Conv2D(c1[0], c1[1], 1, act='relu')
        self.p2_1 = Conv2D(c1[0], c2[0], 1, act='relu')
        self.p2_2 = Conv2D(c2[0], c2[1], 3, padding=1, act='relu')
        self.p3_1 = Conv2D(c1[0], c3[0], 1, act='relu')
        self.p3_2 = Conv2D(c3[0], c3[1], 5, padding=2, act='relu')
        self.p4_1 = Pool2D(pool_size=3, pool_stride=1, pool_padding=1, pool_type='max')
        self.p4_2 = Conv2D(c1[0], c4, 1, act='relu')

    def forward(self, x):
        p1 = self.p1_1(x)
        p2 = self.p2_2(self.p2_1(x))
        p3 = self.p3_2(self.p3_1(x))
        p4 = self.p4_2(self.p4_1(x))

        return fluid.layers.concat([p1, p2, p3, p4], axis=1)

class GoogLeNet(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(GoogLeNet, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 7, padding=3, stride=2, act='relu')
        self.pool1 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.conv2_1 = Conv2D(64, 64, 1, act='relu')
        self.conv2_2 = Conv2D(64, 192, 3, padding=1, act='relu')
        self.pool2 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.block3_a = Inception(self.full_name(), (192, 64), (96, 128), (16, 32), 32)
        self.block3_b = Inception(self.full_name(), (256, 128), (128, 192), (32, 96), 64)
        self.pool3 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.block4_a = Inception(self.full_name(), (480, 192), (96, 208), (16, 48), 64)
        self.block4_b = Inception(self.full_name(), (512, 160), (112, 224), (24, 64), 64)
        self.block4_c = Inception(self.full_name(), (512, 128), (128, 256), (24, 64), 64)
        self.block4_d = Inception(self.full_name(), (512, 112), (144, 288), (32, 64), 64)
        self.block4_e = Inception(self.full_name(), (528, 256), (160, 320), (32, 128), 128)
        self.pool4 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.block5_a = Inception(self.full_name(), (832, 256), (160, 320), (32, 128), 128)
        self.block5_b = Inception(self.full_name(), (832, 384), (192, 384), (48, 128), 128)
        self.pool5 = Pool2D(pool_size=7, pool_stride=1, global_pooling=True, pool_type='avg')
        self.drop = Dropout(p=0.4)
        self.fc = Linear(1024, num_classes)

    def forward(self, x):
        x = self.pool1(self.conv1(x))
        x = self.pool2(self.conv2_2(self.conv2_1(x)))
        x = self.pool3(self.block3_b(self.block3_a(x)))
        x = self.pool4(self.block4_e(self.block4_d(self.block4_c(self.block4_b(self.block4_a(x))))))
        x = self.pool5(self.block5_b(self.block5_a(x)))
        x = self.drop(x)
        x = fluid.layers.reshape(x, [-1, 1024])
        x = self.fc(x)

        return x

#训练过程
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = GoogLeNet("GoogLeNet", num_classes=16)
    train(epoch_num, batch_size, model)

5.对比分析经典模型在Caltech101抽取16类mini版数据集上的效果

1）结果对比

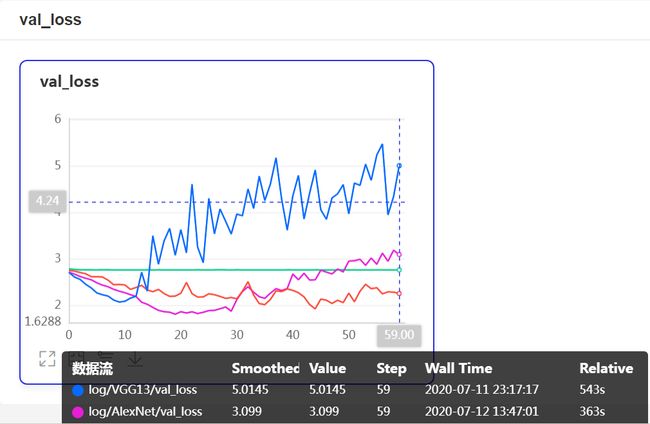
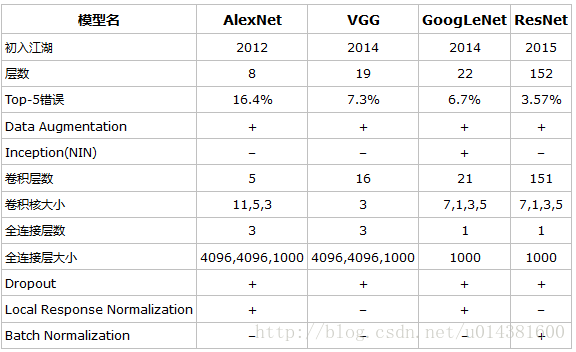
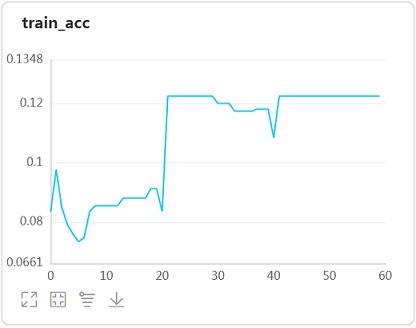
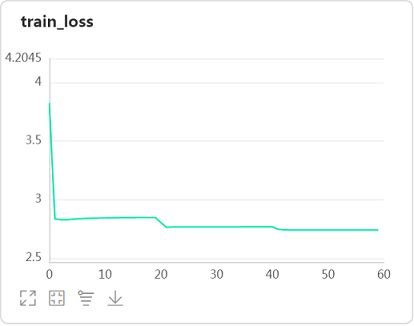
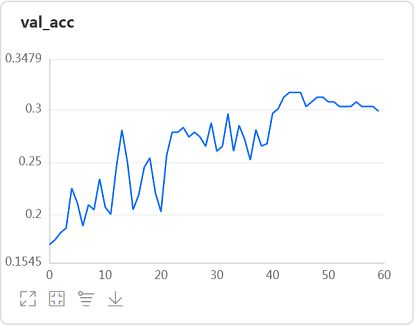
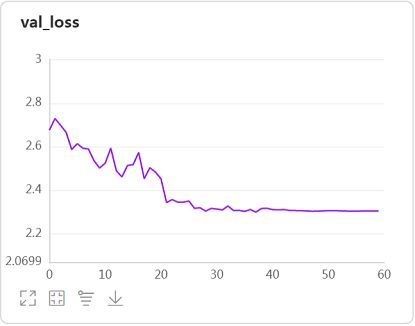
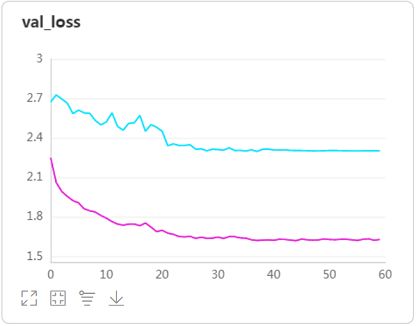
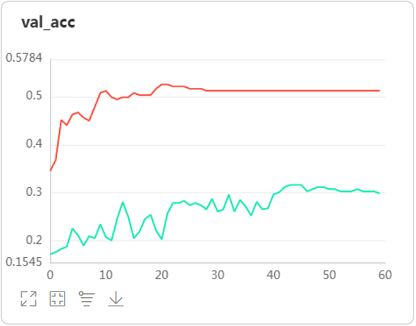
使用VisualDL，查看在batch_size=32，learning_rate=0.001,Momentum优化器条件下各经典模型训练60轮的结果：

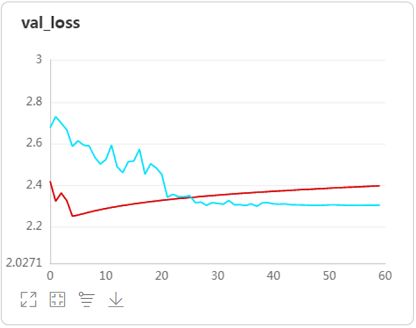
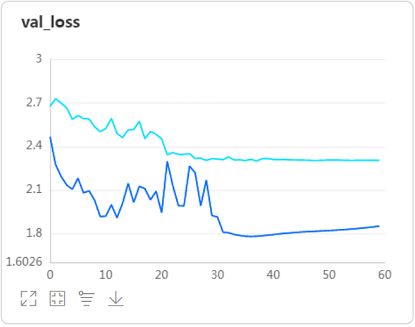
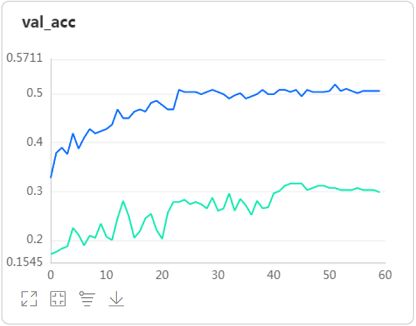
从各个模型在验证集的准确率上看，LeNet是针对32×32尺寸的手写数字识别任务设计的，不适合大尺寸图片的分类任务，模型根本无法收敛。准确率最高的竟然是AlexNet，按理说GoogLeNet和VGG网络更复杂，应该性能更好才是。观察验证集的loss发现，原来VGG网络产生了严重的过拟合。推测可能是VGG使用多层的3×3卷积代替大尺寸的卷积层导致网络层数更多导致的。而GoogLeNet并未产生过拟合，性能的不佳的原因可能是模型收敛比较慢。只有60轮，模型可能训练的不够充分。为了验证这一猜想，下面使用Batch Normalization层加速模型训练。而且BN层也有一定缓解过拟合的效果。所以也试验下能不能提升VGG的性能。

2）使用BN层改进GoogLeNet和VGG

# VGG加BN层抑制过拟合
class VGG_BN(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1, layer=13):
        super(VGG_BN, self).__init__(name_scope)
        name_scope = self.full_name()

        self.layer = layer

        self.pool = Pool2D(pool_size=2, pool_stride=2)
        self.drop_out = Dropout(p=0.5)
        self.bn64 = BatchNorm(64)
        self.bn128 = BatchNorm(128)
        self.bn256 = BatchNorm(256)
        self.bn512 = BatchNorm(512)

        self.conv1 = Conv2D(3, 64, 3, padding=1, act='relu')
        self.conv2 = Conv2D(64, 64, 3, padding=1, act='relu')

        self.conv3 = Conv2D(64, 128, 3, padding=1, act='relu')
        self.conv4 = Conv2D(128, 128, 3, padding=1, act='relu')

        self.conv5 = Conv2D(128, 256, 3, padding=1, act='relu')
        self.conv6 = Conv2D(256, 256, 3, padding=1, act='relu')
        self.conv7 = Conv2D(256, 256, 3, padding=1, act='relu')
        self.conv8 = Conv2D(256, 256, 3, padding=1, act='relu')

        self.conv9 = Conv2D(256, 512, 3, padding=1, act='relu')
        self.conv10 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv11 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv12 = Conv2D(512, 512, 3, padding=1, act='relu')

        self.conv13 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv14 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv15 = Conv2D(512, 512, 3, padding=1, act='relu')
        self.conv16 = Conv2D(512, 512, 3, padding=1, act='relu')

        self.fc1 = Linear(input_dim=512 * 7 * 7, output_dim=4096, act='relu')
        self.fc2 = Linear(input_dim=4096, output_dim=4096, act='relu')
        self.fc3 = Linear(input_dim=4096, output_dim=num_classes)

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        # x = self.bn64(x)
        x = self.conv2(x)
        # x = self.bn64(x)
        x = self.pool(x)

        x = self.conv3(x)
        # x = self.bn128(x)
        x = self.conv4(x)
        x = self.bn128(x)
        x = self.pool(x)

        x = self.conv5(x)
        # x = self.bn256(x)
        x = self.conv6(x)
        # x = self.bn256(x)
        if self.layer >= 16:
            x = self.conv7(x)
            # x = self.bn256(x)
        if self.layer >= 19:
            x = self.conv8(x)
            # x = self.bn256(x)
        x = self.pool(x)

        x = self.conv9(x)
        x = self.bn512(x)
        x = self.conv10(x)
        # x = self.bn512(x)
        if self.layer >= 16:
            x = self.conv11(x)
            # x = self.bn512(x)
        if self.layer >= 19:
            x = self.conv12(x)
            # x = self.bn512(x)
        x = self.pool(x)

        x = self.conv13(x)
        # x = self.bn512(x)
        x = self.conv14(x)
        # x = self.bn512(x)
        if self.layer >= 16:
            x = self.conv15(x)
            # x = self.bn512(x)
        if self.layer >= 19:
            x = self.conv16(x)
            # x = self.bn512(x)
        x = self.pool(x)
 
        x = fluid.layers.reshape(x, [-1, 512 * 7 * 7])
        x = self.fc1(x)
        x = self.drop_out(x)
        x = self.fc2(x)
        x = self.drop_out(x)
        x = self.fc3(x)
        return x

# GoogLeNet加BN层加速模型收敛
class Inception(fluid.dygraph.Layer): # 定义Inception块（Inception v1）
    def __init__(self, name_scope, c1, c2, c3, c4):
        super(Inception, self).__init__(name_scope)
        name_scope = self.full_name()

        self.p1_1 = Conv2D(c1[0], c1[1], 1, act='relu')
        self.p2_1 = Conv2D(c1[0], c2[0], 1, act='relu')
        self.p2_2 = Conv2D(c2[0], c2[1], 3, padding=1, act='relu')
        self.p3_1 = Conv2D(c1[0], c3[0], 1, act='relu')
        self.p3_2 = Conv2D(c3[0], c3[1], 5, padding=2, act='relu')
        self.p4_1 = Pool2D(pool_size=3, pool_stride=1, pool_padding=1, pool_type='max')
        self.p4_2 = Conv2D(c1[0], c4, 1, act='relu')

    def forward(self, x):
        p1 = self.p1_1(x)
        p2 = self.p2_2(self.p2_1(x))
        p3 = self.p3_2(self.p3_1(x))
        p4 = self.p4_2(self.p4_1(x))

        return fluid.layers.concat([p1, p2, p3, p4], axis=1)

class GoogLeNet_BN(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(GoogLeNet_BN, self).__init__(name_scope)
        name_scope = self.full_name()

        self.bn64 = BatchNorm(64)
        self.bn192 = BatchNorm(192)
        self.bn256 = BatchNorm(256)
        self.bn480 = BatchNorm(480)
        self.bn512 = BatchNorm(512)
        self.bn528 = BatchNorm(528)
        self.bn832 = BatchNorm(832)
        self.bn1024 = BatchNorm(1024)

        self.conv1 = Conv2D(3, 64, 7, padding=3, stride=2, act='relu')
        self.pool1 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.conv2_1 = Conv2D(64, 64, 1, act='relu')
        self.conv2_2 = Conv2D(64, 192, 3, padding=1, act='relu')
        self.pool2 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.block3_a = Inception(self.full_name(), (192, 64), (96, 128), (16, 32), 32)
        self.block3_b = Inception(self.full_name(), (256, 128), (128, 192), (32, 96), 64)
        self.pool3 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.block4_a = Inception(self.full_name(), (480, 192), (96, 208), (16, 48), 64)
        self.block4_b = Inception(self.full_name(), (512, 160), (112, 224), (24, 64), 64)
        self.block4_c = Inception(self.full_name(), (512, 128), (128, 256), (24, 64), 64)
        self.block4_d = Inception(self.full_name(), (512, 112), (144, 288), (32, 64), 64)
        self.block4_e = Inception(self.full_name(), (528, 256), (160, 320), (32, 128), 128)
        self.pool4 = Pool2D(pool_size=3, pool_stride=2, pool_padding=1, pool_type='max')
        self.block5_a = Inception(self.full_name(), (832, 256), (160, 320), (32, 128), 128)
        self.block5_b = Inception(self.full_name(), (832, 384), (192, 384), (48, 128), 128)
        self.pool5 = Pool2D(pool_size=7, pool_stride=1, global_pooling=True, pool_type='avg')
        self.drop = Dropout(p=0.4)
        self.fc = Linear(1024, num_classes)

    # 网络的前向计算过程
    def forward(self, x):
        x = self.pool1(self.conv1(x))
        x = self.bn64(x)
        x = self.pool2(self.conv2_2(self.conv2_1(x)))
        # x = self.bn192(x)
        x = self.pool3(self.block3_b(self.block3_a(x)))
        x = self.bn480(x)
        x = self.pool4(self.block4_e(self.block4_d(self.block4_c(self.block4_b(self.block4_a(x))))))
        # x = self.bn832(x)
        x = self.pool5(self.block5_b(self.block5_a(x)))
        x = self.bn1024(x)
        x = self.drop(x)
        x = fluid.layers.reshape(x, [-1, 1024])
        x = self.fc(x)

        return x

# 训练
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = VGG_BN("VGG13_BN", num_classes=16, layer=13)
    train(epoch_num, batch_size, model)
    model = GoogLeNet_BN("GoogLeNet_BN", num_classes=16)
    train(epoch_num, batch_size, model)

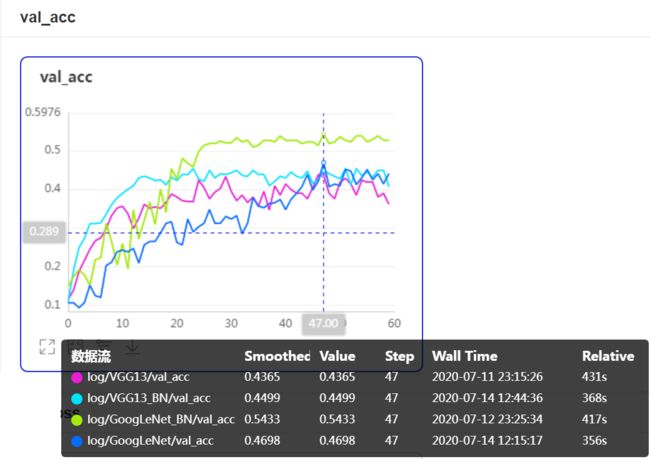
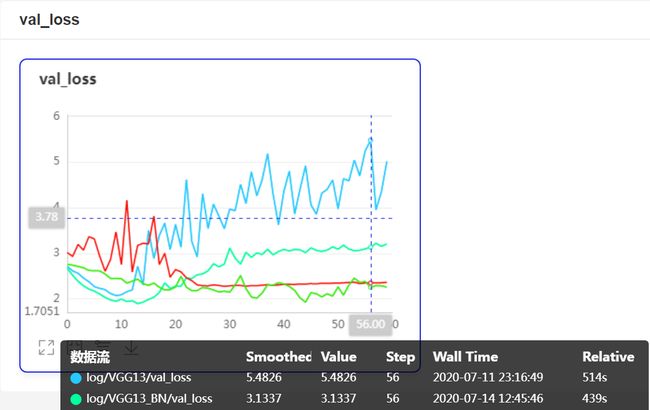
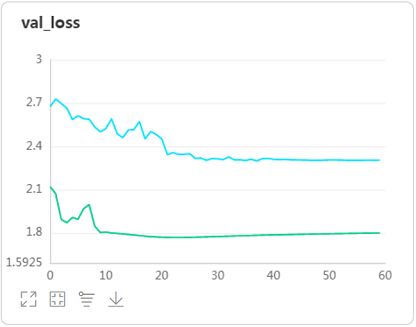
观察VGG和GoogLeNet加入BN层的后的训练结果我们看到：

• 在GoogLeNet的卷积层和Inception块后加入BN层大大加速了模型的收敛，在同样60轮的训练中提升了大概8个点验证集准确率，而且稳定了验证集loss。

• 在VGG卷积层后加入BN层则大大降低了验证集的loss，对过拟合有明显的抑制作用，而且提升了模型的验证集准确率至少1个点。

3）总结分析经典模型

下面这张图概括性的对比了AlexNet、VGG和GoogLeNet（ResNet也被剧透了，因为图片来自网络）

通过跑上面的经典模型我体会到，越是复杂、层数多的模型越难伺候。VGG模型不但对参数的初始权重有要求（最初还要求预训练参数），而且16层、19层的大模型还要分层先后训练。GoogLeNet也需要辅助分类器这根拐棍儿。仿佛这些大型（当时来说）模型的骨架（梯度传播能力）已经要支撑不住自身的重量（网络层数），再往上码就要趴。当然，后来ResNet（华人的骄傲）的横空出世给大伙集体补了钙（通过跨层信息传播），这是后话。大的模型对调参的要求也是更高。有人调侃深度学习网络已经成了“深度调参”网络。

所以，在战场上不是兵刃越大越好，而是要“适合”敌人。在这个项目中，敌人只有16个（16分类），掏出AlexNet直接撂倒，架枪架炮不一定能打到几个。当然，如果敌人上千（ImageNet1000分类任务），还是VGG、GoogleNet这样的重炮、重坦能攻坚，毕竟他们的荣誉也是在那样的竞技场上赢得的。（愿世界和平，同一个世界，同一个梦想。想摸个一筒，介是个一筒，和！【麻将术语读hú】）

下面我们也尝试打造一把称手的兵刃——“如意金箍棒”。

三、手撕CNN

我们的策略是先用最基础的CNN结构搭建一个基线版本，然后逐一尝试前辈的经典模型们给我们留下的各种“神兵利刃”。

1.基线版本（1）

仿照LeNet和AlexNet，根据输入的图片尺寸，用6个5×5的卷积层提取图片特征。中间加入5个大小步长均为2的最大池化层，将输入尺寸为224×224的图片像素特征图逐步缩小至7×7。后面接两个全连接层，用于非线性地选择性激活前面卷积网络中提取特征的神经元。

感谢“李奈”和“爱李奈”为我们奠定了卷积神经网络的基础，否则深度学习将万古如长夜…风头都被SVM、HMM抢去…

# 搭建一个基本的CNN模型
class CNN(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 5, padding=2, stride=1, act='sigmoid')
        self.conv2 = Conv2D(64, 128, 5,padding=2, stride=1, act='sigmoid')
        self.conv3 = Conv2D(128, 256, 5, padding=2, stride=1, act='sigmoid')
        self.conv4 = Conv2D(256, 512, 5, padding=2, stride=1, act='sigmoid')
        self.conv5 = Conv2D(512, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.conv6 = Conv2D(1024, 1024, 5, padding=2, stride=1, act='sigmoid')

        self.fc1 = Linear(1024 * 7 * 7, 1024, act='sigmoid')
        self.fc2 = Linear(1024, num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.pool_down(x)
        x = self.conv5(x)
        x = self.pool_down(x)
        x = self.conv6(x)

        x = fluid.layers.reshape(x, [-1, 1024 * 7 * 7])
        x = self.fc1(x)
        x = self.fc2(x)

        return x

# 训练
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN("CNN_Sigmoid", num_classes=16)
    train(epoch_num, batch_size, model)

观察loss和准确率曲线发现：

• 模型在训练集上都没有收敛。分析这是由于Sigmoid激活函数的曲线特征（靠近上下界走势过缓、取值范围是0～1）和网络层数比较多（比LeNet多）导致了参数在传递过程中不断向一个方向偏移导致梯度消散造成的。

• 考虑解决的办法是使用BN层在每次卷积后将参数的分布修正回来。当然也可以使用曲线更加合理（靠近上下界时仍有一定坡度、取值范围-1～1）的tanh激活函数。下面先尝试使用BN层改进，因为用BN层改善参数分布后还能加速模型训练。

2.加入BN层的基线版本（2）

在每一个卷积层后加入一个BN层。感谢ResNet给我们带来Batch Normalization操作，加速训练又抗过拟合。

class CNN_BaseLine(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN_BaseLine, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 5, padding=2, stride=1, act='sigmoid')
        self.bn1 = BatchNorm(64)
        self.conv2 = Conv2D(64, 128, 5,padding=2, stride=1, act='sigmoid')
        self.bn2 = BatchNorm(128)
        self.conv3 = Conv2D(128, 256, 5, padding=2, stride=1, act='sigmoid')
        self.bn3 = BatchNorm(256)
        self.conv4 = Conv2D(256, 512, 5, padding=2, stride=1, act='sigmoid')
        self.bn4 = BatchNorm(512)
        self.conv5 = Conv2D(512, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.bn5 = BatchNorm(1024)
        self.conv6 = Conv2D(1024, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.bn6 = BatchNorm(1024)

        self.fc1 = Linear(1024 * 7 * 7, 1024, act='sigmoid')
        self.fc2 = Linear(1024, num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.pool_down(x)
        x = self.conv5(x)
        x = self.bn5(x)
        x = self.pool_down(x)
        x = self.conv6(x)
        x = self.bn6(x)

        x = fluid.layers.reshape(x, [-1, 1024 * 7 * 7])
        x = self.fc1(x)
        x = self.fc2(x)

        return x

# 训练
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_BaseLine("CNN_Sigmoid_BN_Baseline", num_classes=16)
    train(epoch_num, batch_size, model)

观察用BN层改进后模型在验证集上的loss和准曲率曲线：

• BN层的加入确实使模型开始收敛，我们就用这个版本作为基线版本。

• 我也测试了将激活函数换为tanh，同样使模型开始收敛。但加入BN还能使模型训练加速，所以选用了BN版本作为基线。

下面我们就以此版本为基线测试以上那些经典模型传给我们的各种“兵刃”了～～

3.用ReLU激活函数替换Sigmoid

感谢“爱李奈”带给我们relu激活函数。但relu也不是万能的，因为单侧抑制的特性，导致有些神经元会一直无法激活。后来的 Leaky ReLU 不再简单的丢弃输出负值后面的神经元，改善了这种“神经元死亡”的现象。所以我们在此使用“leaky_relu”尝试改善CNN的基线版本。

class CNN_LeakyRelu(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN_LeakyRelu, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 5, padding=2, stride=1, act='leaky_relu')
        self.bn1 = BatchNorm(64)
        self.conv2 = Conv2D(64, 128, 5,padding=2, stride=1, act='leaky_relu')
        self.bn2 = BatchNorm(128)
        self.conv3 = Conv2D(128, 256, 5, padding=2, stride=1, act='leaky_relu')
        self.bn3 = BatchNorm(256)
        self.conv4 = Conv2D(256, 512, 5, padding=2, stride=1, act='leaky_relu')
        self.bn4 = BatchNorm(512)
        self.conv5 = Conv2D(512, 1024, 5, padding=2, stride=1, act='leaky_relu')
        self.bn5 = BatchNorm(1024)
        self.conv6 = Conv2D(1024, 1024, 5, padding=2, stride=1, act='leaky_relu')
        self.bn6 = BatchNorm(1024)

        self.fc1 = Linear(1024 * 7 * 7, 1024, act='leaky_relu')
        self.fc2 = Linear(1024, num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.pool_down(x)
        x = self.conv5(x)
        x = self.bn5(x)
        x = self.pool_down(x)
        x = self.conv6(x)
        x = self.bn6(x)

        x = fluid.layers.reshape(x, [-1, 1024 * 7 * 7])
        x = self.fc1(x)
        x = self.fc2(x)

        return x

# 训练
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_LeakyRelu("CNN_LeakyRelu", num_classes=16)
    train(epoch_num, batch_size, model)

观察训练结果发现：

• 使用Leaky ReLU激活函数替换基线版本的Sigmiod，不但大幅提高了验证集的准确率十几个点，而且还能在使用了BN层的基础上进一步加快模型的训练。

• 在测试过程中，也测试了使用了普通的ReLU的效果，比Leaky ReLU差一些，但明显好于Sigmiod。

4.用全局平均池化替换全链接层

感谢“咕咕奈”提供的这个trick。用池化代替全连接层不但能提高模型性能，而且能大大降低参数数量。这也是GoogLeNet这样复杂的网络的参数量比VGG甚至AlexNet参数量还少的原因之一。

class CNN_PoolReplaceFC(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN_PoolReplaceFC, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 5, padding=2, stride=1, act='sigmoid')
        self.bn1 = BatchNorm(64)
        self.conv2 = Conv2D(64, 128, 5,padding=2, stride=1, act='sigmoid')
        self.bn2 = BatchNorm(128)
        self.conv3 = Conv2D(128, 256, 5, padding=2, stride=1, act='sigmoid')
        self.bn3 = BatchNorm(256)
        self.conv4 = Conv2D(256, 512, 5, padding=2, stride=1, act='sigmoid')
        self.bn4 = BatchNorm(512)
        self.conv5 = Conv2D(512, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.bn5 = BatchNorm(1024)
        self.conv6 = Conv2D(1024, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.bn6 = BatchNorm(1024)
        
        # 用此处的全局平均池化代替原来的全连接层
        self.pool_global = Pool2D(pool_stride=1, global_pooling=True, pool_type='avg')
        self.fc = Linear(input_dim=1024, output_dim=num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.pool_down(x)
        x = self.conv5(x)
        x = self.bn5(x)
        x = self.pool_down(x)
        x = self.conv6(x)
        x = self.bn6(x)

        x = self.pool_global(x)
        x = fluid.layers.reshape(x, [-1, 1024])
        x = self.fc(x)

        return x

# 训练
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_PoolReplaceFC("CNN_PoolReplaceFC", num_classes=16)
    train(epoch_num, batch_size, model)

观察训练结果发现：

• 用池化替换全连接层后，模型在验证集上的准曲率提升了近二十五个点。（是这次项目中提升最大的处理）

5.使用DropOut

感谢“爱李奈”带给我们的 drop out 这种对付过拟合的方法。drop out一般在全连接层前使用。使用drop out按设定的比例随机丢弃部分神经元的操作，实际上相当于训练了多个网络，并取平均。因此在降低过拟合的同时，也会降低训练速度。

class CNN_DropOut(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN_DropOut, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 5, padding=2, stride=1, act='sigmoid')
        self.bn1 = BatchNorm(64)
        self.conv2 = Conv2D(64, 128, 5,padding=2, stride=1, act='sigmoid')
        self.bn2 = BatchNorm(128)
        self.conv3 = Conv2D(128, 256, 5, padding=2, stride=1, act='sigmoid')
        self.bn3 = BatchNorm(256)
        self.conv4 = Conv2D(256, 512, 5, padding=2, stride=1, act='sigmoid')
        self.bn4 = BatchNorm(512)
        self.conv5 = Conv2D(512, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.bn5 = BatchNorm(1024)
        self.conv6 = Conv2D(1024, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.bn6 = BatchNorm(1024)

        self.fc1 = Linear(1024 * 7 * 7, 1024, act='sigmoid')
        self.fc2 = Linear(1024, num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
        # 按照50%的比例随机丢弃部分神经元
        self.dropout = Dropout(p=0.5)

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.pool_down(x)
        x = self.conv5(x)
        x = self.bn5(x)
        x = self.pool_down(x)
        x = self.conv6(x)
        x = self.bn6(x)

        x = fluid.layers.reshape(x, [-1, 1024 * 7 * 7])
        x = self.fc1(x)
        x = self.dropout(x)
        x = self.fc2(x)

        return x

with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_DropOut("CNN_DropOut", num_classes=16)
    train(epoch_num, batch_size, model)

观察训练结果发现：

• 使用drop out按50%比例进行神经元随机丢弃处理后，模型在验证集上的准确率提升了将近二十个点，而且验证集loss曲线下降的更为平缓，这就是drop out抑制过拟合、取平均的效果。

6.使用两层3×3卷积代替一层5×5卷积核

感谢“V哥哥奈”为我们证明了多层小尺寸卷积核的卷积层的效果好于一层大卷积核的卷积层的效果。后来的网络一般都使用3×3的小卷积核，除非有特殊需求。连GoogLeNet的Inception模块也将5×5的卷积层用两层3×3的卷积层代替。如今，为了进一步减少模型的参数规模，已经开始在追求推理速度的模型中使用1×3的卷积层和3×1的卷积层代替一层3×3的卷积层。

class CNN_CoreSize3(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN_CoreSize3, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 3, padding=1, stride=1, act='sigmoid')
        self.bn1 = BatchNorm(64)
        self.conv1_2 = Conv2D(64, 64, 3, padding=1, stride=1, act='sigmoid')
        self.bn1_2 = BatchNorm(64)
        self.conv2 = Conv2D(64, 128, 3,padding=1, stride=1, act='sigmoid')
        self.bn2 = BatchNorm(128)
        self.conv2_2 = Conv2D(128, 128, 3,padding=1, stride=1, act='sigmoid')
        self.bn2_2 = BatchNorm(128)
        self.conv3 = Conv2D(128, 256, 3, padding=1, stride=1, act='sigmoid')
        self.bn3 = BatchNorm(256)
        self.conv3_2 = Conv2D(256, 256, 3, padding=1, stride=1, act='sigmoid')
        self.bn3_2 = BatchNorm(256)
        self.conv4 = Conv2D(256, 512, 3, padding=1, stride=1, act='sigmoid')
        self.bn4 = BatchNorm(512)
        self.conv4_2 = Conv2D(512, 512, 3, padding=1, stride=1, act='sigmoid')
        self.bn4_2 = BatchNorm(512)
        self.conv5 = Conv2D(512, 1024, 3, padding=1, stride=1, act='sigmoid')
        self.bn5 = BatchNorm(1024)
        self.conv5_2 = Conv2D(1024, 1024, 3, padding=1, stride=1, act='sigmoid')
        self.bn5_2 = BatchNorm(1024)
        self.conv6 = Conv2D(1024, 1024, 3, padding=1, stride=1, act='sigmoid')
        self.bn6 = BatchNorm(1024)
        self.conv6_2 = Conv2D(1024, 1024, 3, padding=1, stride=1, act='sigmoid')
        self.bn6_2 = BatchNorm(1024)

        self.fc1 = Linear(1024 * 7 * 7, 1024, act='sigmoid')
        self.fc2 = Linear(1024, num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.conv1_2(x)
        x = self.bn1_2(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.conv2_2(x)
        x = self.bn2_2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.conv3_2(x)
        x = self.bn3_2(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.conv4_2(x)
        x = self.bn4_2(x)
        x = self.pool_down(x)
        x = self.conv5(x)
        x = self.bn5(x)
        x = self.conv5_2(x)
        x = self.bn5_2(x)
        x = self.pool_down(x)
        x = self.conv6(x)
        x = self.bn6(x)
        x = self.conv6_2(x)
        x = self.bn6_2(x)

        x = fluid.layers.reshape(x, [-1, 1024 * 7 * 7])
        x = self.fc1(x)
        x = self.fc2(x)

        return x

# 训练
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_CoreSize3("CNN_CoreSize3", num_classes=16)
    train(epoch_num, batch_size, model)

观察训练结果发现：

• 在卷积层数量和BN层数量都增加一倍的情况下，模型的准确率提升了将近二十个点。VGG证明的多个小尺寸卷积层优于一个大尺寸卷积层的理论果然所言非虚。前面在尝试给VGG和GoogleNet加入BN层时发现，加两三个BN层可提高模型准确率，再多加的话反而会降低准曲率。

7.使用多尺度卷积拼接模块

其实就是简版的Inception v1块。这种模块可以在不增加网络层数的情况下，使模型只在这一层中就可自动选择激活不同大小感受野的神经元。前面VGG模型可能就是因为层数太多了，反而在只有16个类别的分类任务中表现反而不如更简单的AlexNet。再次感谢“咕咕奈”。

# 此模块将感受野为1×1、3×3、5×5的卷积层拼接在一起，使网络在这一层中就可以自动选择激活不同感受野的神经元
class ConcatConv(fluid.dygraph.Layer):
    def __init__(self, name_scope, c1, c2, c3, c4, act_fun='sigmoid'):
        super(ConcatConv, self).__init__(name_scope)
        name_scope = self.full_name()

        self.p1_1 = Conv2D(c1[0], c1[1], 1, act=act_fun)
        self.p2_1 = Conv2D(c1[0], c2[0], 1, act=act_fun)
        self.p2_2 = Conv2D(c2[0], c2[1], 3, padding=1, act=act_fun)
        self.p3_1 = Conv2D(c1[0], c3[0], 1, act=act_fun)
        self.p3_2 = Conv2D(c3[0], c3[1], 5, padding=2, act=act_fun)
        self.p4_1 = Pool2D(pool_size=3, pool_stride=1, pool_padding=1, pool_type='max')
        self.p4_2 = Conv2D(c1[0], c4, 1, act=act_fun)

    def forward(self, x):
        p1 = self.p1_1(x)
        p2 = self.p2_2(self.p2_1(x))
        p3 = self.p3_2(self.p3_1(x))
        p4 = self.p4_2(self.p4_1(x))

        return fluid.layers.concat([p1, p2, p3, p4], axis=1)

class CNN_ConcatConv(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN_ConcatConv, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 5, padding=2, stride=1, act='sigmoid')
        self.bn1 = BatchNorm(64)
        self.conv2 = Conv2D(64, 128, 5,padding=2, stride=1, act='sigmoid')
        self.bn2 = BatchNorm(128)
        self.conv3 = Conv2D(128, 256, 5, padding=2, stride=1, act='sigmoid')
        self.bn3 = BatchNorm(256)
        self.conv4 = Conv2D(256, 512, 5, padding=2, stride=1, act='sigmoid')
        self.bn4 = BatchNorm(512)
        self.block5 = ConcatConv(self.full_name(), (512, 384), (384, 256), (256, 256), 128)
        self.bn5 = BatchNorm(1024)
        self.conv6 = Conv2D(1024, 1024, 5, padding=2, stride=1, act='sigmoid')
        self.bn6 = BatchNorm(1024)

        self.fc1 = Linear(1024 * 7 * 7, 1024, act='sigmoid')
        self.fc2 = Linear(1024, num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
        self.dropout = Dropout(p=0.5)

    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.pool_down(x)
        x = self.block5(x)
        x = self.bn5(x)
        x = self.pool_down(x)
        x = self.conv6(x)
        x = self.bn6(x)

        x = fluid.layers.reshape(x, [-1, 1024 * 7 * 7])
        x = self.fc1(x)
        x = self.dropout(x)
        x = self.fc2(x)

        return x

# 训练
with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_ConcatConv("CNN_ConcatConv", num_classes=16)
    train(epoch_num, batch_size, model)

观察训练结果发现：

• 验证集准确率提升二十五个点，验证集loss曲线下降得非常漂亮。还能说什么呢？只能用“滔滔江水”表达崇敬之情。

8.十八般兵刃都融了，我们要造金箍棒!

我们在这个CNN模型中：

• 使用6个卷积层（后两个替换为多尺度拼接的ConcatConv模块）提取图像特征

• 每个卷积层后加一个BN层整理数值分布

• 最后一个卷积层后使用全局平均池化

• 池化后进行一个50%比例的drop out

• 最后接一个全连接层输出16分类结果

• 所有的卷积层和全连接层包括拼接的ConcatConv模块内均使用Leaky ReLU激活函数

# 此模块将感受野为1×1、3×3、5×5的卷积层拼接在一起，使网络在这一层中就可以自动选择激活不同感受野的神经元
class ConcatConv(fluid.dygraph.Layer):
    def __init__(self, name_scope, c1, c2, c3, c4, act_fun='sigmoid'):
        super(ConcatConv, self).__init__(name_scope)
        name_scope = self.full_name()

        self.p1_1 = Conv2D(c1[0], c1[1], 1, act=act_fun)
        self.p2_1 = Conv2D(c1[0], c2[0], 1, act=act_fun)
        self.p2_2 = Conv2D(c2[0], c2[1], 3, padding=1, act=act_fun)
        self.p3_1 = Conv2D(c1[0], c3[0], 1, act=act_fun)
        self.p3_2 = Conv2D(c3[0], c3[1], 5, padding=2, act=act_fun)
        self.p4_1 = Pool2D(pool_size=3, pool_stride=1, pool_padding=1, pool_type='max')
        self.p4_2 = Conv2D(c1[0], c4, 1, act=act_fun)

    def forward(self, x):
        p1 = self.p1_1(x)
        p2 = self.p2_2(self.p2_1(x))
        p3 = self.p3_2(self.p3_1(x))
        p4 = self.p4_2(self.p4_1(x))

        return fluid.layers.concat([p1, p2, p3, p4], axis=1)

class CNN_AllTricks(fluid.dygraph.Layer):
    def __init__(self, name_scope, num_classes=1):
        super(CNN_AllTricks, self).__init__(name_scope)
        name_scope = self.full_name()

        self.conv1 = Conv2D(3, 64, 3, padding=1, stride=1, act='leaky_relu')
        self.bn1 = BatchNorm(64)
        self.conv2 = Conv2D(64, 128, 3,padding=1, stride=1, act='leaky_relu')
        self.bn2 = BatchNorm(128)
        self.conv3 = Conv2D(128, 256, 3, padding=1, stride=1, act='leaky_relu')
        self.bn3 = BatchNorm(256)
        self.conv4 = Conv2D(256, 512, 3, padding=1, stride=1, act='leaky_relu')
        self.bn4 = BatchNorm(512)
        self.block5 = ConcatConv(self.full_name(), (512, 384), (384, 256), (256, 256), 128, act_fun='leaky_relu')
        self.bn5 = BatchNorm(1024)
        self.block6 = ConcatConv(self.full_name(), (1024, 384), (384, 256), (256, 256), 128, act_fun='leaky_relu')
        self.bn6 = BatchNorm(1024)

        self.pool_global = Pool2D(pool_stride=1, global_pooling=True, pool_type='avg')
        self.fc = Linear(input_dim=1024, output_dim=num_classes)

        self.pool_down = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
        self.dropout = Dropout(p=0.5)

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.pool_down(x)
        x = self.block5(x)
        x = self.bn5(x)
        x = self.pool_down(x)
        x = self.block6(x)
        x = self.bn6(x)

        x = self.pool_global(x)
        x = fluid.layers.reshape(x, [-1, 1024])
        x = self.dropout(x)
        x = self.fc(x)

        return x

with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_AllTricks("CNN_AllTricks", num_classes=16)
    # train(epoch_num, batch_size, model)
    train(epoch_num, batch_size, model, lr_decay=True)
(p=0.5)

    # 网络的前向计算过程
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.pool_down(x)
        x = self.conv2(x)
        x = self.bn2(x)
        x = self.pool_down(x)
        x = self.conv3(x)
        x = self.bn3(x)
        x = self.pool_down(x)
        x = self.conv4(x)
        x = self.bn4(x)
        x = self.pool_down(x)
        x = self.block5(x)
        x = self.bn5(x)
        x = self.pool_down(x)
        x = self.block6(x)
        x = self.bn6(x)

        x = self.pool_global(x)
        x = fluid.layers.reshape(x, [-1, 1024])
        x = self.dropout(x)
        x = self.fc(x)

        return x

with fluid.dygraph.guard(fluid.CUDAPlace(0)):
    model = CNN_AllTricks("CNN_AllTricks", num_classes=16)
    # train(epoch_num, batch_size, model)
    train(epoch_num, batch_size, model, lr_decay=True)

观察训练结果发现：

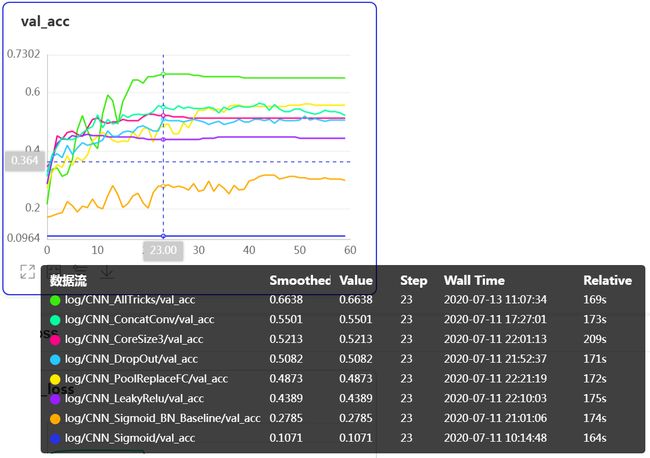
七个葫芦娃（还真是前边七个模型合成一个，哈哈）合体的金刚葫芦娃果然比哪个都厉害，验证集最高准确率达到了66%。在没有使用L2正则化项、数据增强等手段的情况下将模型的基线版本的验证集准确率提升了一倍多。

四、总结

• 细心的同学会发现，上面葫芦娃牌儿的金箍棒在“炼化”的过程中和前面的模型有点儿不一样，train（）函数中增加了一个lr_decay=True参数。是的，我在训练最后这个 CNN_AllTricks 模型时采取了学习率分段衰减的方式。如果不衰减学习率，模型的准确率能达到将近60%。这也印证了前面的观点：越复杂的模型越需要调参。当然，我也对前面的七个CNN模型同样用过学习率衰减的方式训练，并没有显著的提高。这就印证了最后 CNN_AllTricks 分类能力的提高来自于前面模型里各种trick的融合，而非调参。

• 在调整CNN模型结构的过程中，我尝试了增减卷积层、BN层和自己改造的ConcatConv模块的数量，发现再增加网络的深度不但不能提升反而会降低模型的效果。参照VGG和GoogLeNet可以堆到二十层左右，这个CNN模型还十层不到，应该还可以改进。我想如果使用L2正则化项和数据增强抑制过拟合的话，模型深度应该还可以加深。只是重复试验比较麻烦，考虑能不能使用Paddle Slim的Light-NAS自动搜索网络结构。恳请大佬指点。

• 在试验各种CNN结构与技巧的过程中，我发现了一个有趣的网站（ http://playground.tensorflow.org）。 可以在上面直观的通过增加、删除神经元的数量来观察网络深度、广度对拟合各种分类曲线的影响。还可以调整L2正则化项参数，直观地观察该参数对过拟合的抑制作用。

• 这个项目我也使用“化妆品8分类数据集”验证了一下有效性。在不使用L2正则化项和数据增强的情况下CNN模型的分类准确率可以到80%以上。为了突出本项目的重点，我没有将训练结果保存在这个项目中。有兴趣的同学也可以到（https://aistudio.baidu.com/aistudio/projectdetail/626708） 看看这些tricks在“化妆品8分类数据集”上的效果。上面也保留了使用数据增强的代码。

这个“卷积网络第一篇”项目介绍的都是卷积网络中基础，属于拳拳到肉的功夫。下一篇“介绍ResNet一族”的项目里的功夫就挣脱了“深度网络梯度消失”的束缚，挥出了天马流星拳。百层、千层的网络不是梦，从此限制网络深度的只有你的想象力和买显卡的魄力…

注:以上经典模型和自造CNN模型的训练log已经分别存储在“log_classical”和“log_cnn“文件夹中，如果想通过VisualDL的web页面查看，只需将它们的文件夹名依次改为“log”后，就可依次查看了。

代码可在百度AI Studio上使用免费算力运行。项目地址：https://aistudio.baidu.com/aistudio/projectdetail/601071

百度AI Studio有送免费算力的活动
我发现了一个炒鸡棒的AI学习与实训社区！为我助力赢10小时免费算力，助力成功您可领100小时哦～ https://aistudio.baidu.com/aistudio/newbie?invitation=1&sharedUserId=76563&sharedUserName=FutureSI