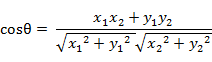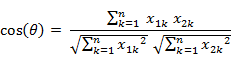【推荐系统算法实战】协同过滤 CF 算法（Collaborative Filtering）

什么是协同过滤算法？

协同过滤推荐（Collaborative Filtering Recommendation）。

仅仅基于用户行为数据设计的推荐算法一般称为协同过滤算法。学术界对协同过滤算法 进行了深入研究，提出了很多方法，比如基于邻域的方法(neighborhood-based)、隐语义模型 (latent factor model)、基于图的随机游走算法(random walk on graph)等。在这些方法中， 最著名的、在业界得到最广泛应用的算法是基于邻域的方法。

协同过滤，从字面上理解，包括协同和过滤两个操作。所谓协同就是利用群体的行为来做决策(推荐)，生物上有协同进化的说法，通过协同的作用，让群体逐步进化到更佳的状态。对于推荐系统来说，通过用户的持续协同作用，最终给用户的推荐会越来越准。而过滤，就是从可行的决策(推荐)方案(标的物)中将用户喜欢的方案(标的物)找(过滤)出来。

协同进化（coevolution）：两个相互作用的物种在进化过程中发展的相互适应的共同进化。一个物种由于另一物种影响而发生遗传进化的进化类型。例如一种植物由于食草昆虫所施加的压力而发生遗传变化，这种变化又导致昆虫发生遗传性变化。
协同进化是生物与环境的交互关系，是一种协同关系，古生物学的物种是形态种，在一定程序上与交配群的概念是一致的。物种又是生态单位。隔离成种的理论与多地区成种并不矛盾。生态系与基因的协同作用表现在多方面，生态系的变动会影响基因，生物的相互作用也影响基因。地球表层是由多个圈层组成，生物圈与其他各圈层有密切关系。“第二生物圈”试验的失败说明，到目前为止人为的“生物圈”不可能完全替代地球生物圈的作用。

具体来说，协同过滤的思路是通过群体的行为来找到某种相似性(用户之间的相似性或者标的物之间的相似性)，通过该相似性来为用户做决策和推荐。

现实生活中有很多协同过滤的案例及思想体现，除了前面提到的生物的进化是一种”协同过滤“作用外，我认为人类喜欢追求相亲中的“门当户对”，其实也是一种协同过滤思想的反射，门当户对实际上是建立了相亲男女的一种“相似度”(家庭背景、出身、生活习惯、为人处世、消费观、甚至价值观可能会相似)，给自己找一个门当户对的伴侣就是一种“过滤”，当双方”门当户对“时，各方面的习惯及价值观会更相似，未来幸福的概率也会更大。如果整个社会具备这样的传统和风气，以及在真实”案例“中”门当户对“的夫妻确实会更和谐，通过”协同进化“作用，大家会越来越认同这种方式。我个人也觉得”门当户对“是有一定道理的。

协同过滤利用了两个非常朴素的自然哲学思想：“群体的智慧”和“相似的物体具备相似的性质”，群体的智慧从数学上讲应该满足一定的统计学规律，是一种朝向平衡稳定态发展的动态过程，越相似的物体化学及物理组成越一致，当然表现的外在特性会更相似。虽然这两个思想很简单，也很容易理解，但是正因为思想很朴素，价值反而非常大。所以协同过滤算法原理很简单，但是效果很不错，而且也非常容易实现。

协同过滤分为基于用户的协同过滤和基于标的物(物品)的协同过滤两类算法。下面我们对协同过滤的算法原理来做详细的介绍。

推荐算法种类很多，但是目前应用最广泛的就是协同过滤算法。

协同过滤简单来说是利用某兴趣相投、拥有共同经验之群体的喜好来推荐用户感兴趣的信息，个人通过合作的机制给予信息相当程度的回应（如评分）并记录下来以达到过滤的目的进而帮助别人筛选信息，回应不一定局限于特别感兴趣的，特别不感兴趣信息的纪录也相当重要。

协同过滤又可分为评比（rating）或者群体过滤（social filtering）协同过滤以其出色的速度和健壮性，在全球互联网领域炙手可热。

电子商务的推荐系统

最著名的电子商务推荐系统应属亚马逊网络书店，顾客选择一本自己感兴趣的书籍，马上会在底下看到一行

“Customer Who Bought This Item Also Bought”

亚马逊是在“对同样一本书有兴趣的读者们兴趣在某种程度上相近”的假设前提下提供这样的推荐，此举也成为亚马逊网络书店为人所津津乐道的一项服务，各网络书店也跟进做这样的推荐服务如台湾的博客来网络书店。

另外一个著名的例子是Facebook的广告，系统根据个人资料、周遭朋友感兴趣的广告等等对个人提供广告推销，也是一项协同过滤重要的里程碑，和前二者Tapestry、GroupLens不同的是在这里虽然商业气息浓厚同时还是带给使用者很大的方便。 以上为三项协同过滤发展上重要的里程碑，从早期单一系统内的邮件、文件过滤，到跨系统的新闻、电影、音乐过滤，乃至于横行互联网的电子商务，虽然目的不太相同，但带给使用者的方便是大家都不能否定的。

算法原理

数据结构（数据模型）

协同过滤的模型一般为m个物品，m个用户的数据，只有部分用户和部分数据之间是有评分数据的，其它部分评分是空白，此时我们要用已有的部分稀疏数据来预测那些空白的物品和数据之间的评分关系，找到最高评分的物品推荐给用户。

一般来说，协同过滤推荐分为三种类型:

第一种是基于用户(user-based)的协同过滤;
第二种是基于项目(item-based)的协同过滤;
第三种是基于模型(model based)的协同过滤。

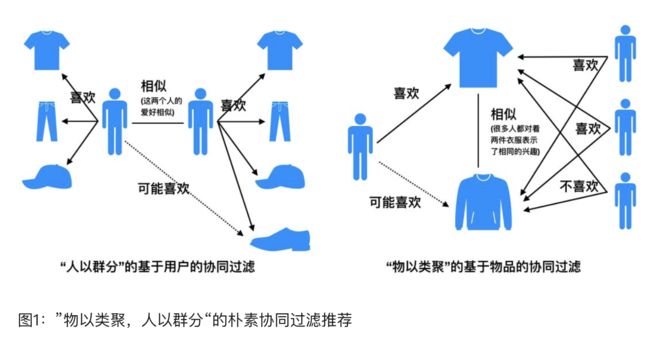
基于用户(user-based)的协同过滤主要考虑的是用户和用户之间的相似度，只要找出相似用户喜欢的物品，并预测目标用户对对应物品的评分，就可以找到评分最高的若干个物品推荐给用户。而基于项目(item-based)的协同过滤和基于用户的协同过滤类似，只不过这时我们转向找到物品和物品之间的相似度，只有找到了目标用户对某些物品的评分，那么我们就可以对相似度高的类似物品进行预测，将评分最高的若干个相似物品推荐给用户。比如你在网上买了一本机器学习相关的书，网站马上会推荐一堆机器学习，大数据相关的书给你，这里就明显用到了基于项目的协同过滤思想。

我们可以简单比较下基于用户的协同过滤和基于项目的协同过滤：基于用户的协同过滤需要在线找用户和用户之间的相似度关系，计算复杂度肯定会比基于基于项目的协同过滤高。但是可以帮助用户找到新类别的有惊喜的物品。而基于项目的协同过滤，由于考虑的物品的相似性一段时间不会改变，因此可以很容易的离线计算，准确度一般也可以接受，但是推荐的多样性来说，就很难带给用户惊喜了。一般对于小型的推荐系统来说，基于项目的协同过滤肯定是主流。但是如果是大型的推荐系统来说，则可以考虑基于用户的协同过滤，当然更加可以考虑我们的第三种类型，基于模型的协同过滤。

基于模型(model based)的协同过滤是目前最主流的协同过滤类型了，我们的一大堆机器学习算法也可以在这里找到用武之地。

算法（函数）

基于用户的协同过滤算法描述

基于用户的协同过滤算法的实现主要需要解决两个问题，一是如何找到和你有相似爱好的人，也就是要计算数据的相似度：

计算相似度需要根据数据特点的不同选择不同的相似度计算方法，有几个常用的计算方法：

（1）杰卡德相似系数(Jaccard similarity coefficient)

其实就是集合的交集除并集

（2）夹角余弦(Cosine)

在二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦：

即 　　　　　　　　　　　　　　

（3）其余方法，例如欧式距离、曼哈顿距离等相似性度量方法可以点此了解

找到与目标用户最相邻的K个用户

我们在寻找有有相同爱好的人的时候，可能会找到许多个，例如几百个人都喜欢A商品，但是这几百个人里，可能还有几十个人与你同时还喜欢B商品，他们的相似度就更高，我们通常设定一个数K，取计算相似度最高的K个人称为最相邻的K个用户，作为推荐的来源群体。

这里存在一个小问题，就是当用户数据量十分巨大的时候，在所有人之中找到K个基友花的时间可能会比较长，而且实际中大部分的用户是和你没有什么关系的，所以在这里需要用到反查表

所谓反查表，就是比如你喜欢的商品有A、B、C，那就分别以ABC为行名，列出喜欢这些商品的人都有哪些，其他的人就必定与你没有什么相似度了，从这些人里计算相似度，找到K个人

通过这K个人推荐商品

我们假设找到的人的喜好程度如下

	A	B	C	D
甲（相似度25%）	√	√		√
乙（相似度80%）			√	√

那么对于产品ABCD，推荐度可以计算为：

●A：1*0.25=0.25

●B：1*0.25=0.25

●C：1*0.8=0.8

●D：10.25+10.8=1.05

很明显，我们首先会推荐D商品，其次是C商品，再后是其余商品

当然我们也可以采用其他的推荐度计算方法，但是我们一定会使用得到的相似度0.25和0.80，也即一定是进行加权的计算。

算法总结

这就是基于用户的协同推荐算法，总结步骤为

1.计算其他用户的相似度，可以使用反查表除掉一部分用户

2.根据相似度找到与你嘴相似的K个用户

3.在这些邻居喜欢的物品中，根据与你的相似度算出每一件物品的推荐度

4.根据相似度推荐物品

Mahout 实践

在现实中广泛使用的推荐系统一般都是基于协同过滤算法的，这类算法通常都需要计算用户与用户或者项目与项目之间的相似度，对于数据量以及数据类型不同的数据源，需要不同的相似度计算方法来提高推荐性能，在mahout提供了大量用于计算相似度的组件，这些组件分别实现了不同的相似度计算方法。下图用于实现相似度计算的组件之间的关系：

图1、项目相似度计算组件

图2、用户相似度计算组件

下面就几个重点相似度计算方法做介绍：

皮尔森相关度

类名：PearsonCorrelationSimilarity

原理：用来反映两个变量线性相关程度的统计量

范围：[-1,1]，绝对值越大，说明相关性越强，负相关对于推荐的意义小。

说明：1、 不考虑重叠的数量；2、 如果只有一项重叠，无法计算相似性（计算过程被除数有n-1）；3、 如果重叠的值都相等，也无法计算相似性（标准差为0，做除数）。

该相似度并不是最好的选择，也不是最坏的选择，只是因为其容易理解，在早期研究中经常被提起。使用Pearson线性相关系数必须假设数据是成对地从正态分布中取得的，并且数据至少在逻辑范畴内必须是等间距的数据。Mahout中，为皮尔森相关计算提供了一个扩展，通过增加一个枚举类型（Weighting）的参数来使得重叠数也成为计算相似度的影响因子。

欧式距离相似度

类名：EuclideanDistanceSimilarity

原理：利用欧式距离d定义的相似度s，s=1 / (1+d)。

范围：[0,1]，值越大，说明d越小，也就是距离越近，则相似度越大。

说明：同皮尔森相似度一样，该相似度也没有考虑重叠数对结果的影响，同样地，Mahout通过增加一个枚举类型（Weighting）的参数来使得重叠数也成为计算相似度的影响因子。

余弦相似度

类名：PearsonCorrelationSimilarity和UncenteredCosineSimilarity

原理：多维空间两点与所设定的点形成夹角的余弦值。

范围：[-1,1]，值越大，说明夹角越大，两点相距就越远，相似度就越小。

说明：在数学表达中，如果对两个项的属性进行了数据中心化，计算出来的余弦相似度和皮尔森相似度是一样的，在mahout中，实现了数据中心化的过程，所以皮尔森相似度值也是数据中心化后的余弦相似度。另外在新版本中，Mahout提供了UncenteredCosineSimilarity类作为计算非中心化数据的余弦相似度。

Spearman秩相关系数

类名：SpearmanCorrelationSimilarity

原理：Spearman秩相关系数通常被认为是排列后的变量之间的Pearson线性相关系数。

范围：{-1.0,1.0}，当一致时为1.0，不一致时为-1.0。

说明：计算非常慢，有大量排序。针对推荐系统中的数据集来讲，用Spearman秩相关系数作为相似度量是不合适的。

曼哈顿距离

类名：CityBlockSimilarity

原理：曼哈顿距离的实现，同欧式距离相似，都是用于多维数据空间距离的测度

范围：[0,1]，同欧式距离一致，值越小，说明距离值越大，相似度越大。

说明：比欧式距离计算量少，性能相对高。

Tanimoto系数

类名：TanimotoCoefficientSimilarity

原理：又名广义Jaccard系数，是对Jaccard系数的扩展，等式为

范围：[0,1]，完全重叠时为1，无重叠项时为0，越接近1说明越相似。

说明：处理无打分的偏好数据。

对数似然相似度

类名：LogLikelihoodSimilarity

原理：重叠的个数，不重叠的个数，都没有的个数

范围：具体可去百度文库中查找论文《Accurate Methods for the Statistics of Surprise and Coincidence》

说明：处理无打分的偏好数据，比Tanimoto系数的计算方法更为智能。

推荐算法评测指标

参考资料

https://www.cnblogs.com/chenliyang/p/6548306.html

---

Kotlin 开发者社区

国内第一Kotlin 开发者社区公众号，主要分享、交流 Kotlin 编程语言、Spring Boot、Android、React.js/Node.js、函数式编程、编程思想等相关主题。

越是喧嚣的世界，越需要宁静的思考。