《吴恩达机器学习》笔记:第二章:多维特征,梯度下降和正规方程
多维特征(Multiple features)
将线性模型从一维拓展到多维
- n:代表特征的个数
- m:代表观测的个数(此处与通常习惯不同)
- x ( i ) x^{(i)} x(i):第 i i i个样本的输入向量
- x j ( i ) x_{j}^{(i)} xj(i):第 i i i个样本的输入的特征 j j j
将一元线性模型进行拓展:
h θ ( x ) = θ 0 + θ 1 x 1 + … + θ n x n h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\ldots+\theta_{n} x_{n} hθ(x)=θ0+θ1x1+…+θnxn
为了形式方便,定义 x 0 = 1 x_{0} = 1 x0=1
h θ ( x ) = θ 0 x 0 + θ 1 x 1 + … + θ n x n h_{\theta}(x)=\theta_{0} x_{0}+\theta_{1} x_{1}+\ldots+\theta_{n} x_{n} hθ(x)=θ0x0+θ1x1+…+θnxn
定义矩阵形式:
X = [ x 0 x 1 x 2 ⋮ x n ] ∈ R n + 1 , Θ = [ θ 0 θ 1 θ 2 ⋮ θ n ] ∈ R n + 1 X=\left[\begin{array}{c}x_{0} \\ x_{1} \\ x_{2} \\ \vdots \\ x_{n}\end{array}\right] \in \mathbb{R}^{n+1} , \Theta=\left[\begin{array}{c}\theta_{0} \\ \theta_{1} \\ \theta_{2} \\ \vdots \\ \theta_{n}\end{array}\right] \in \mathbb{R}^{n+1} X=⎣⎢⎢⎢⎢⎢⎡x0x1x2⋮xn⎦⎥⎥⎥⎥⎥⎤∈Rn+1,Θ=⎣⎢⎢⎢⎢⎢⎡θ0θ1θ2⋮θn⎦⎥⎥⎥⎥⎥⎤∈Rn+1
其中:
Θ : ( n + 1 ) × 1 X : ( n + 1 ) × m \Theta: (n + 1) \times1 \\ X:(n + 1) \times m Θ:(n+1)×1X:(n+1)×m
则
h θ ( x ) = Θ T X h_{\theta}(x)=\Theta^{T} X hθ(x)=ΘTX
多维梯度下降(Gradient Descent for multiple variables)
我们不难从多元模型中得到,
需要优化的参数: θ 0 , θ 1 . . . θ n \theta_0 ,\theta_1...\theta_n θ0,θ1...θn
损失函数:
损失函数为实际与模型的残差平方和
J ( θ 0 , θ 1 , … , θ n ) = 1 2 m ∑ i m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)=\frac{1}{2 m} \sum_{i}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J(θ0,θ1,…,θn)=2m1i∑m(hθ(x(i))−y(i))2
其中:
h θ ( x ) = θ 0 + θ 1 x 1 + … + θ n x n h_{\theta}(x)=\theta_{0}+\theta_{1} x_{1}+\ldots+\theta_{n} x_{n} hθ(x)=θ0+θ1x1+…+θnxn
根据之前以为梯度下降函数,不难求得多维梯度下降的计算公式
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 , … , θ n ) \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right) θj:=θj−α∂θj∂J(θ0,θ1,…,θn)
带入损失函数:
θ j : = θ j − α ∂ ∂ θ j 1 2 m ∑ i m ( h θ ( x ( i ) ) − y ( i ) ) 2 : = θ j − α 1 2 m ∑ i m ( h θ ( x ( i ) ) − y ( i ) ) 2 x j ( i ) \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} \frac{1}{2 m} \sum_{i}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} \\ :=\theta_{j}-\alpha \frac{1}{2 m} \sum_{i}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} x_{j}^{(i)} θj:=θj−α∂θj∂2m1∑im(hθ(x(i))−y(i))2:=θj−α2m1∑im(hθ(x(i))−y(i))2xj(i)
对于每一个变量,迭代上述过程,即可求得最终值
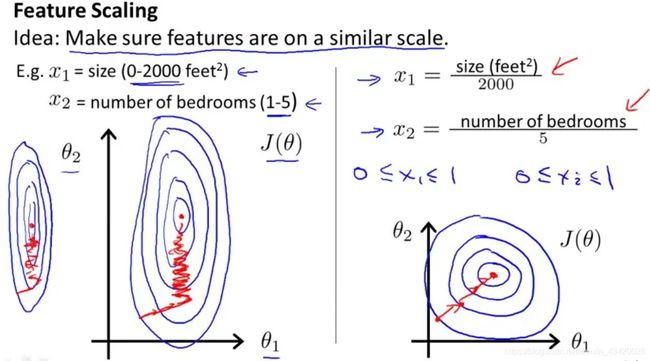
特征缩放(Feature Scaling)
使得所有的特征都处于一个相近的范围,使得梯度下降算法能够更快的收敛
若特征量纲差距较大,以代价函数绘制的等高线图类似于椭圆形,梯度下降算法需要多次迭代才能求得真实值。
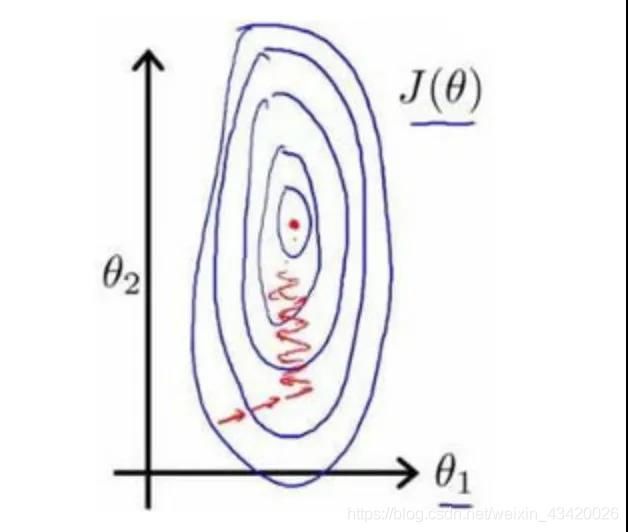
解决方法: 均值归一化
x n = x n − u n s n x_{n}=\frac{x_{n}-u_{n}}{s_{n}} xn=snxn−un
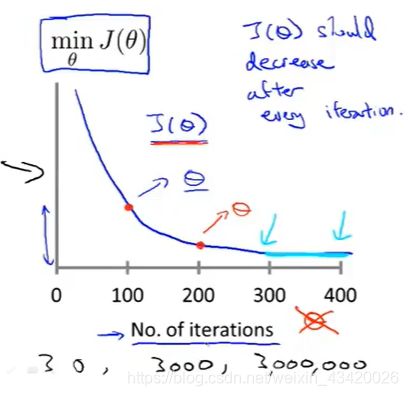
学习率 α \alpha α:
- 如果学习率过小,则达到收敛所需的迭代次数会非常高,收敛速度非常慢
- 如果学习率过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛
常用学习率: 0.01 , 0.03 , 0.1 , 0.3 , 1 , 3 , 10 0.01, 0.03,0.1,0.3,1,3,10 0.01,0.03,0.1,0.3,1,3,10
合适的学习率:
过大的学习率:
损失函数不收敛
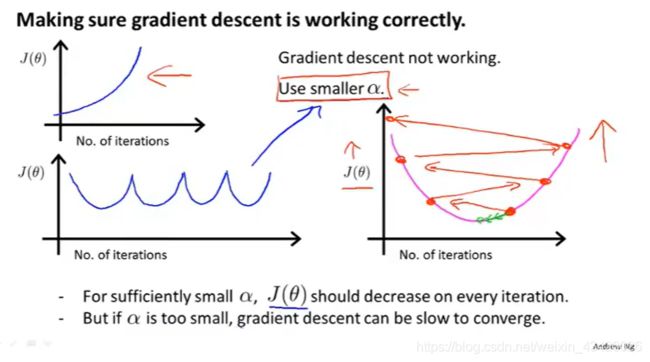
过小的学习率:
收敛速度很慢
非线性模型:
在实际拟合数据的时候,我们很可能会选择二次或者三次方模型;如果采用多项式回归模型,在运行梯度下降法之前,特征缩放很有必要。
正规方程(Normal Equation)
解析法求解参数 θ \theta θ
对于损失函数
J ( θ 0 , θ 1 , … , θ n ) = 1 2 m ∑ i m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left(\theta_{0}, \theta_{1}, \ldots, \theta_{n}\right)=\frac{1}{2 m} \sum_{i}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J(θ0,θ1,…,θn)=2m1i∑m(hθ(x(i))−y(i))2
使得
∂ ∂ θ j J ( θ ) = . . . = 0 (for every j ) \frac{\partial}{\partial \theta_{j}} J\left(\theta\right)=...=0\text{ (for every }j\text{)} ∂θj∂J(θ)=...=0 (for every j)
求解过程:
-
将表达式转换为矩阵表达式,有 J ( θ ) = 1 2 ( X θ − y ) 2 J\left(\theta\right)=\frac{1}{2 } \left({X\theta}-y\right)^{2} J(θ)=21(Xθ−y)2,其中
- X X X为 m m m行 n n n列的矩阵(m个样本,n个特征)
- θ \theta θ为 n n n行1列的矩阵
- y y y为 m m m行1列的矩阵
-
对 J ( θ ) J(\theta) J(θ)变换:
J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta)=\frac{1}{2}(X \theta-y)^{T}(X \theta-y) J(θ)=21(Xθ−y)T(Xθ−y)
= 1 2 ( θ T X T − y T ) ( X θ − y ) =\frac{1}{2}\left(\theta^{T} X^{T}-y^{T}\right)(X \theta-y) =21(θTXT−yT)(Xθ−y)
= 1 2 ( θ T X T X θ − θ T X T y − y T X θ − y T y ) =\frac{1}{2}\left(\theta^{T} X^{T} X \theta-\theta^{T} X^{T} y-y^{T} X \theta-y^{T} y\right) =21(θTXTXθ−θTXTy−yTXθ−yTy) -
对 J ( θ ) J(\theta) J(θ)求偏导,使用矩阵求导法则:
d A B d B = A T \frac{d A B}{d B}=A^{T} dBdAB=AT , d X T A X d X = 2 A X \frac{d X^{T} A X}{d X}=2 A X dXdXTAX=2AX
-
求导得到:
∂ J ( θ ) ∂ θ = 1 2 ( 2 X T X θ − X T y − ( y T X ) T − 0 ) \frac{\partial J(\theta)}{\partial \theta}=\frac{1}{2}\left(2 X^{T} X \theta-X^{T} y-\left(y^{T} X\right)^{T}-0\right) ∂θ∂J(θ)=21(2XTXθ−XTy−(yTX)T−0)
= 1 2 ( 2 X T X θ − X T y − X T y − 0 ) =\frac{1}{2}\left(2 X^{T} X \theta-X^{T} y-X^{T} y-0\right) =21(2XTXθ−XTy−XTy−0)
= X T X θ − X T y =X^{T} X \theta-X^{T} y =XTXθ−XTy -
若要 ∂ J ( θ ) ∂ θ = 0 \frac{\partial J(\theta)}{\partial \theta}=0 ∂θ∂J(θ)=0
则 X T X θ − X T y = 0 X^{T} X \theta-X^{T} y=0 XTXθ−XTy=0
解得:
θ = ( X T X ) − 1 X T y \theta=\left(X^{T} X\right)^{-1} X^{T} y θ=(XTX)−1XTy
特殊情况
( X T X ) − 1 \left(X^{T} X\right)^{-1} (XTX)−1不可逆:
- 变量线性相关(完全多重共线)
- 特征过多,观测过少( m < = n m<=n m<=n)
-可以删除变量或使用正则化(regularization)
正规方程vs梯度下降
| 梯度下降 | 正规方程 |
|---|---|
| 需要学习率 α \alpha α | 不需要学习率 α \alpha α |
| 需要多次迭代 | 一次计算得出 |
| 即使特征很多的时候表现也很好 | 由于需要计算 ( X T X ) − 1 \left(X^{T} X\right)^{-1} (XTX)−1,特征多会很慢,矩阵求逆计算复杂度为 O ( n 3 ) O(n^3) O(n3) ,通常用于n小于10000 |
| 适用于各种模型 | 只适用于线性模型 |
参考
机器学习-吴恩达
