《吴恩达机器学习》笔记:第一章:机器学习基础
机器学习基础
机器学习定义:在没有明确设置的情况下,使得计算机具有学习能力的研究领域。
E = the experience of playing many games of checkers
T = the task of playing checkers
P = the probability that the program will win the next game
监督学习和无监督学习
监督学习(supervised learning)
回归问题
在监督学习中,我们给学习算法一个数据集,给定数据集中每个样本的正确值,然后通过运用学习算法,能够计算出一系列连续的答案,这属于回归问题
利用监督学习预测波士顿房价(回归问题)
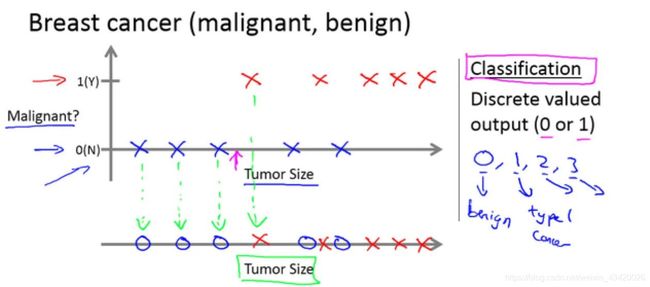
分类问题
分类问题指,目标是推测出离散的输出值:0或1,也有可能输出值不止两个
- 横轴肿瘤大表示小
- 纵轴1表示恶性,0表示良性
无监督学习(unsupervised learning)
- 监督学习中,数据是有标签的
- 无监督学习中,数据是没有标签
单变量线性回归(Linear Regression with One Variable)
以上文的房价预测为例
学习过程:
- 将训练集中的房屋数据(TrainingSet)输入算法
- 算法返回一个模型,Model:h,是基于训练集训练的模型
- Model:h代表的是算法学习得到的模型
- h根据输入的x值得到y值,因此Model:h是x到的y的一个函数映射
- 可能的表达式: h θ ( x ) = θ 0 + θ 1 x h_θ(x)=θ_0+θ_1x hθ(x)=θ0+θ1x,单变量线性回归问题
代价函数(cost function)
代价函数又称为平方误差函数,平方误差代价函数。
在线性回归中我们有一个像这样的训练集,m代表了训练样本的数量,比如 m = 47 m=47 m=47。我们假设真实模型也为线性形式: h θ ( x ) = θ 0 + θ 1 x h_θ(x)=θ_0+θ_1x hθ(x)=θ0+θ1x。
参数解释
- m m m:训练样本个数
- h θ ( x ) = θ 0 + θ 1 x h_θ(x)=θ_0+θ_1x hθ(x)=θ0+θ1x:设定模型
- θ 0 θ0 θ0和 θ 1 θ1 θ1:表示两个模型参数,即斜率和截距
模型求解
- 真实值 y i y_i yi,真实的数据集
- h ( x ) h(x) h(x)表示的是通过模型得到的预测值
- 目标:选择出可以使得建模误差的平方和 J ( θ 0 , θ 1 ) J\left(\theta_{0}, \theta_{1}\right) J(θ0,θ1)能够最小的模型参数
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
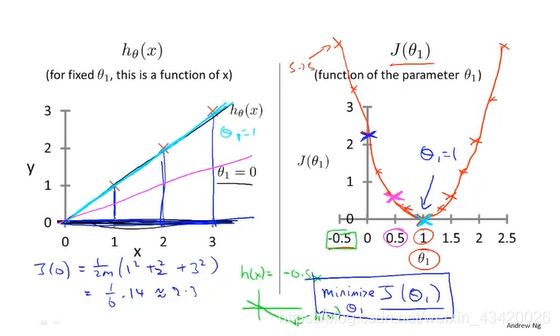
一维代价函数
本例假设模型中 θ 0 = 0 θ_0=0 θ0=0,假设函数 h ( x ) h(x) h(x)是关于 x x x的函数,代价函数 J ( θ 1 ) J\left(\theta_{1}\right) J(θ1)是关于 θ 1 \theta_{1} θ1的函数,目标是使得代价函数最小化
H y p o t h e s i s : h θ ( x ) = θ 1 x Hypothesis:h_{\theta}(x)=\theta_{1} x Hypothesis:hθ(x)=θ1x
P a r a m e t e r s : θ 1 Parameters:\theta_{1} Parameters:θ1
C o s t F u n c t i o n : J ( θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 Cost Function: J\left(\theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} CostFunction:J(θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
G o a l : minimize θ 1 J ( θ 1 ) Goal: \operatorname{minimize}_{ \theta_{1}} J\left( \theta_{1}\right) Goal:minimizeθ1J(θ1)
二维代价函数
通过三维图来进行解释。通过绘制出三维图可以看出来,必定存在某个点,使得代价函数(Cost Function)最小,即三维空间中的最低点
H y p o t h e s i s : h θ ( x ) = θ 0 + θ 1 x Hypothesis:h_{\theta}(x)=\theta_{0}+\theta_{1} x Hypothesis:hθ(x)=θ0+θ1x
P a r a m e t e r s : θ 0 , θ 1 Parameters:\theta_{0},\theta_{1} Parameters:θ0,θ1
C o s t F u n c t i o n : J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 Cost Function: J\left(\theta_{0},\theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} CostFunction:J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
G o a l : minimize θ 0 , θ 1 J ( θ 0 , θ 1 ) Goal: \operatorname{minimize}_{ \theta_{0},\theta_{1}} J\left( \theta_{0},\theta_{1}\right) Goal:minimizeθ0,θ1J(θ0,θ1)

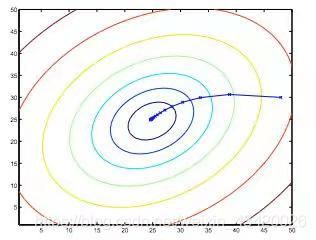
梯度下降(Gradient Descent)
思想
梯度下降是一个用来求函数最小值的算法。
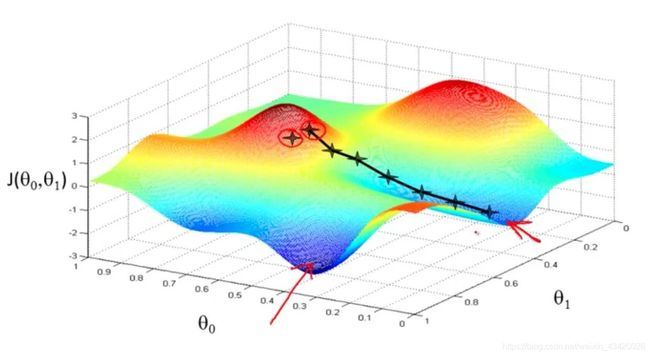
核心思想:开始随机选取一个参数的组合 ( θ 0 , θ 1 , … , θ n ) (θ_0,θ_1,…,θ_n) (θ0,θ1,…,θn)计算代价函数,然后找到使得函数下降速度最快的参数组合,持续这么做,直到找到一个局部最小值,因为并没有尝试完所有的参数组合,所以不能确定得到的局部最小值是否是全局最小值
下图为两个局部最小值:
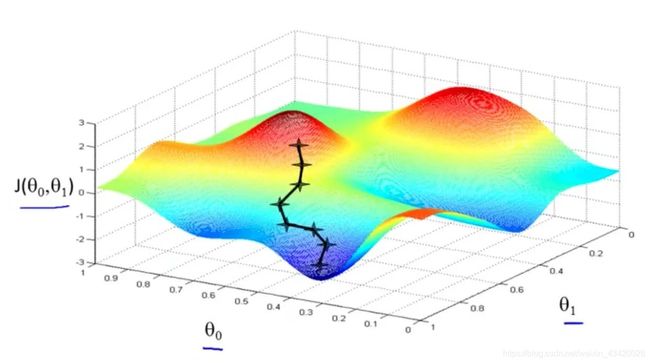
选取另一个起始点,获得不同的局部最小值:
算法公式:
梯度下降算法:
repeat until convergence { \text { repeat until convergence }\{ repeat until convergence {
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( for j = 0 and j = 1 ) \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right) \quad(\text { for } j=0 \text { and } j=1) θj:=θj−α∂θj∂J(θ0,θ1)( for j=0 and j=1)
} \} }
同步更新(一定先计算两个temp):
temp 0 : = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) 0:=\theta_{0}-\alpha \frac{\partial}{\partial \theta_{0}} J\left(\theta_{0}, \theta_{1}\right) 0:=θ0−α∂θ0∂J(θ0,θ1)
temp 1 : = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) 1:=\theta_{1}-\alpha \frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right) 1:=θ1−α∂θ1∂J(θ0,θ1)
θ 0 : = \theta_{0}:= θ0:= temp 0
θ 1 : = \theta_{1}:= θ1:= temp 1
参数解释:
α : \alpha: α:学习速率,控制梯度下降的速度,决定了我们沿着能让代价函数下降程度最大的方向向下前进的距离
∂ J ( θ 0 , θ 1 ) ∂ θ j : \frac{\partial J\left(\theta_{0}, \theta_{1}\right)}{\partial \theta_{j}}: ∂θj∂J(θ0,θ1):导数项,决定梯度下降的方向
计算过程:
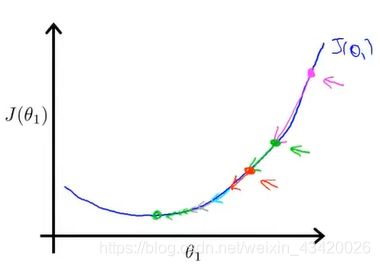
对 θ θ θ赋初始值,使得 J ( θ ) J(θ) J(θ)按照梯度下降最快的方向进行,一直迭代,直到最终得到局部最小值(实际操作中采用当步长小于临界值)。
参数过大过小可能出现的问题:
- 学习率太小:收敛速度过慢可能需要很长的时间才会到达全局最低点
- 学习率太大:收敛速度过快可能越过最低点,导致无法收敛

即使对于固定的学习速率 α \alpha α,梯度下降也能收敛到局部最小值。因为当接近局部最小值时,梯度下降算法会自动采取更小的幅度(对函数本身有要求),所以不需要时刻减小 α \alpha α。
梯度下降应用于线性回归:
结合梯度下降算法和线性回归模型用来拟合数据

多维梯度下降算法:
求解梯度下降模型,关键在于将导数项转为递推形式
∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)=\frac{\partial}{\partial \theta_{j}} \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} ∂θj∂J(θ0,θ1)=∂θj∂2m1∑i=1m(hθ(x(i))−y(i))2
j = 0 j=0 j=0 时: ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial}{\partial \theta_{0}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) ∂θ0∂J(θ0,θ1)=m1∑i=1m(hθ(x(i))−y(i))
j = 1 j=1 j=1 时: ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ) \frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x^{(i)}\right) ∂θ1∂J(θ0,θ1)=m1∑i=1m((hθ(x(i))−y(i))⋅x(i))
循环形式:
repeat until convergence { \text { repeat until convergence }\{ repeat until convergence {
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \theta_{0}:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) \theta_{1}:=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x^{(i)} θ1:=θ1−αm1∑i=1m(hθ(x(i))−y(i))⋅x(i)
} \} }
这种梯度下降的算法称为多维梯度下降算法,观察算法表达是,我们不难看出以下特点:
在梯度下降的每一步中,我们都用到了所有的训练样本,导数项本质是样本的一阶或二阶表达式,因为在计算微分求导项时,我们需要进行求和运算,需要对所有 m m m个训练样本求和
参考
机器学习-吴恩达