遗传算法中常见遗传算子
遗传算法中常见遗传算子
- 常见选择算子
-
- 轮盘选择(roulette wheel selection)
- 随机遍历抽样(Stochastic universal sampling,SUS)
- 排序选择(rank-based selection)
- 适应度缩放选择(Fitness scaling)
- 锦标赛选择(Tournament selection)
- 常见交叉算子
-
- 单点交叉(Single-point crossover)
- k点交叉(K-point crossover)
- 均匀交叉(Uniform crossover)
- 用于有序列表的交叉
-
- 有序交叉
- 常见变异算子
-
- 位翻转突变(Flip bit mutation)
- 交换突变
- 反转突变(Swap mutation)
- 倒换突变(Inversion mutation)
- 常见用于实数编码染色体的遗传算子
-
- 混合交叉(blend crossover)
- 模拟二进制交叉(simulated binary crossover)
- 实数突变
常见选择算子
在遗传算法流程的每个循环的开始,利用选择算子从当前种群中选出个体,这些个体作为下一代个体的双亲。该选择是基于概率的,并且被选中的个体的概率与其适应度相关联,从而有较高适应度的个体具有更高优势。
轮盘选择(roulette wheel selection)
在轮盘选择(也称为适应比例选择,fitness proportionate selection,FPS)中,选择一个个体的概率与其适应度值直接成正比。这相当于在娱乐场中使用轮盘并为每个轮盘的一部分分配适应度值。转动轮盘时,每个个体被选中的几率与轮盘所占部分的大小成正比。
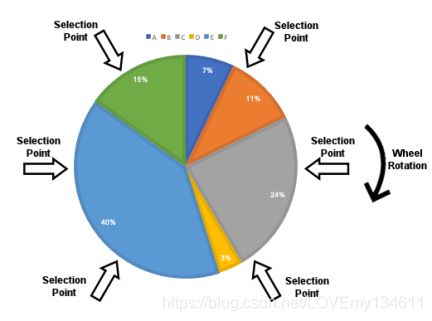
例如,假设我们有六个具有适应度值的个体,如下表所示。基于以下适合度值,计算每个个体对应轮盘的相应部分:
| 个体 | 适应度 | 相对占比 |
|---|---|---|
| A | 8 | 7% |
| B | 12 | 11% |
| C | 27 | 24% |
| D | 4 | 3% |
| E | 45 | 40% |
| F | 17 | 15% |
相应的轮盘如下:

每次转动转盘时,选择点均用于从整个种群中选择一个个体。然后再次转动轮子,选择下一个个体,直到选择了足够的个体来产生下一代。因此,同一个个体可以被多次选中。
随机遍历抽样(Stochastic universal sampling,SUS)
随机遍历抽样是先前描述的轮盘选择的修改版本。使用相同的轮盘,比例相同,但使用多个选择点,只旋转一次转盘就可以同时选择所有个体:
这种选择方法可以防止个体被过分反复选择,从而避免了具有特别高适应度的个体垄断下一代。因此,它为较低适应度的个体提供了被选择的机会,从而减少了原始轮盘选择方法的不公平性。
排序选择(rank-based selection)
排序选择方法类似于轮盘选择,但不是直接使用适应度值来计算选择每个个体的概率,而是将适应度用于对个体进行排序。排序后,将为每个人指定代表其位置的等级,并根据这些等级计算轮盘概率。
例如,以先前使用的六个个体作为样本。由于在示例中种群规模为6,排名最高的个人的排名值为6,下一个人口的排名值为5,依此类推。根据这些排名值计算每个个体对应的轮盘的部分:
| 个体 | 适应度 | 排名 | 相对占比 |
|---|---|---|---|
| A | 8 | 2 | 9% |
| B | 12 | 3 | 14% |
| C | 27 | 5 | 24% |
| D | 4 | 1 | 5% |
| E | 45 | 6 | 29% |
| F | 17 | 4 | 19% |
对应的轮盘:

当某些个体的适应度值比其他人大得多时,排序选择会很有用。由于排名消除了适应度值的巨大差异,因此使用排名代替原始适应度可以防止这几个个体垄断下一代。
同样,当所有个体都具有相似的适应度值时,基于排名的选择会增加它们之间的差异,为较好的个体带来明显的优势。
适应度缩放选择(Fitness scaling)
适应度缩放将缩放转换应用于原始适应度,将原始适应度值映射到所需范围 [ a , b ] [a,b] [a,b]:
s c a l e d f i t n e s s = a × ( r a w f i t n e s s ) + b scaled fitness = a × (raw fitness) + b scaledfitness=a×(rawfitness)+b
实现缩放的适应度在期望范围内,例如,先前示例中的原始适应度值的范围在4到45之间。假设想将值映射到介于50和100之间的新范围。可以使用以下方程式(分别代表适应度最低和最高的两个个体)来计算a和b常数的值:
50 = a × 4 + b 100 = a × 45 + b 50 = a × 4 + b \\ 100 = a × 45 + b 50=a×4+b100=a×45+b
解决这个线性方程组将得到以下缩放参数值:
a = 1.22 , b = 45.12 a = 1.22, b = 45.12 a=1.22,b=45.12
然后可以按以下方式计算缩放后的适应度值:
s c a l e d f i t n e s s = 1.22 × ( r a w f i t n e s s ) + 45.12 scaled fitness = 1.22 × (raw fitness) + 45.12 scaledfitness=1.22×(rawfitness)+45.12
在表中添加缩放后的适应度值的新列:
| 个体 | 适应度 | 缩放后的适应度 | 相对占比 |
|---|---|---|---|
| A | 8 | 50 | 13% |
| B | 12 | 60 | 15% |
| C | 27 | 78 | 19% |
| D | 4 | 50 | 12% |
| E | 45 | 100 | 25% |
| F | 17 | 66 | 16% |
如图所示,将适应度值缩放到新范围可提供比原始分区更合适的轮盘分区。现在,选择最佳个体的可能性仅是最差个个体的2倍,而在原始适应度轮盘中最佳适应度者时被选择的可能性较最差个体高11倍以上。
锦标赛选择(Tournament selection)
在锦标赛选择方法的每一轮中,从总体中随机选择两个或多个个体,其中适应度得分最高的获胜并被选中。
例如,假设使用与前面示例中相同的六个个体和相同的适用度值。下图说明了随机选择其中三个(A,B和F),F作为获胜者,因为F在这三个个体中具有最大适应度值:

参加每个锦标赛选择回合的个体数量(示例中为3个)称为锦标赛规模。规模越大,最好的个人参加比赛的机会就越高,得分低的个人赢得比赛并被选中的机会就越小。
这种选择方法的优势在于,只要可以比较任意两个个体并确定其中哪个更好,就不需要适应度函数的实际值。
常见交叉算子
交叉操作,也称为重组,用于结合双亲的遗传信息,以产生(通常是两个)后代。
交叉操作通常使用一些(高)概率值。只要不应用交叉,父母双方都会直接克隆到下一代。
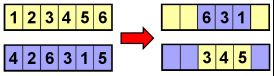
单点交叉(Single-point crossover)
在单点交叉法中,随机选择双亲染色体上的位置。此位置称为交叉点(crossover point)或切割点(cut point)。该点右边的基因在双亲染色体之间交换,得到了两个后代,每个后代都携带着双亲的一些遗传信息。
下图说明了在一对二进制染色体上进行的单点交叉操作,交叉点位于第五个和第六个基因之间:
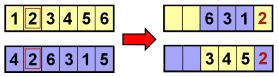
k点交叉(K-point crossover)
k点交叉是单点交叉的扩展,在交叉过程中使用k个交叉点,其中k表示正整数。
下图是k=2时的k点交叉示例,第一个交叉点位于第三和第四基因之间,另一个位于第七和第八个基因之间:

均匀交叉(Uniform crossover)
在均匀交换中,每个基因是通过随机选择一个亲本独立确定的。当随机分布为50%时,每个父母都有影响后代的机会相同:

Note: 在此示例中,第二个后代是通过对第一代后代的选择进行求补而创建的,但是,两个后代也可以彼此独立地创建。
由于这种方法不必交换染色体的全部片段,因此其后代具有更大的多样性。
用于有序列表的交叉
在前面的示例中,我们在两个基于整数的染色体上进行交叉操作,虽然0到9之间的每个值都在每个亲本上出现一次,但是每个后代都有某些值出现多次,而其他值则丢失了。
考虑到在某些任务中,基于整数的染色体可能代表有序列表的索引。例如在旅行商问题中——假设有几个城市,我们知道每个城市之间的距离,并且需要找到穿过所有城市的最短路线。
假设有四个城市,则表示此问题的可能解的简便方法是构造访问城市顺序的具有四位整数染色体的,例如(1,2,3,4)或(3,4,2,1)。具有两个相同值或缺少某些值的染色体诸如(1,2,2,4)是无效的。
对于这种情况,需要设计其他交叉方法以确保创建的后代仍然有效,如有序交叉。
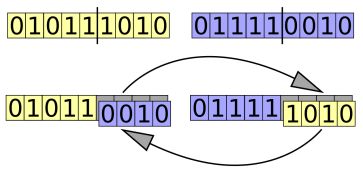
有序交叉
有序交叉(OX1)方法致力于尽可能保留亲本基因的相对顺序。
第一步是具有随机切割点的两点交叉:
从第二个切割点之后开始,按原始顺序遍历所有父母的基因,开始填充每个后代中的其余基因。对于第一个双亲,6是下一个基因,但是在后代中已经存在,因此继续(环绕)到1,这也已经存在,下一个位置是2。由于后代中尚不存在2,因此将其添加到该位置,如下图所示。对于第二对亲子代,从5开始但其在子代中已经存在,然后移至4也同样存在,当移动到2时,后代中并不存在,因此将其添加到子代中:
对于第一个双亲,继续到3(已经存在于后代中),然后是4(后代中并不存在),将其添加到后代中。对于另一个亲本,下一个基因是6。由于对应的后代中不存在该基因,因此将其添加到其中:

以类似的方式继续处理后续基因,并填写下一个可用位点,如下图所示:

常见变异算子
变异算子应用于由于选择和交叉操作而产生的后代。
突变是基于概率的,并且通常以(非常)低的概率发生,因为它带有损害应用此算子个体表现的风险。在遗传算法的某些版本中,随着世代的发展,突变概率逐渐增加,以进化防止停滞并确保种群的多样性。另一方面,如果突变率过度增加,则遗传算法将变成与随机搜索等效的算法。
位翻转突变(Flip bit mutation)
将位翻转突变应用于二进制染色体时,随机选择一个基因,其值被翻转(求补):
![]()
这可以扩展到多个随机基因的翻转,而不仅仅是一个。
交换突变
将交换突变应用于基于二进制或整数的染色体时,将随机选择两个基因并交换其值:
![]()
此突变操作适用于有序列表的染色体,因为新染色体仍带有与原始染色体相同的基因。
反转突变(Swap mutation)
将反转突变应用于基于二进制或整数的染色体时,将选择一个随机的基因序列,并且该序列中的基因顺序颠倒:
![]()
与交换突变类似,反转突变操作适用于有序列表的染色体。
倒换突变(Inversion mutation)
适用于有序列表的染色体的另一种变异算子是倒换变异。应用后,将选择一个随机基因序列,并将该序列中的基因顺序打乱(或倒换):
![]()
常见用于实数编码染色体的遗传算子
到目前为止,已经看到了代表二进制或整数参数的染色体。遗传算子适合于处理这些类型的染色体。但是,我们经常遇到解空间连续的问题。换句话说,个体由实数(浮点数)组成。
遗传算法可以使用二进制串来表示整数和实数,但是使用二进制串表示的实数的精度受串长度(位数)的限制。由于需要提前确定该长度,因此最终可能由于二进制串太短导致精度不足或编码过长。
使用实数值数组代替二进制串是一种更简单,更好的方法。例如,如果遇到涉及三个实值参数的问题,则染色体可以设计为[x1,x2,x3],其中x1,x2,x3表示实数,如[1.23,7.2134,-25.309]或[-30.10,100.2,42.424]。
前述选择方法对于实数编码的染色体同样起作用,因为它们仅取决于个体的适应度,而不取决于其表现形式。
但是,之前介绍的交叉和突变方法不适用于实数编码的染色体,因此需要使用专门的方法。需要记住的重要一点是,这些交叉和突变操作是分别应用于构成实编码染色体的阵列的每个维度的。例如,如果为交叉操作选择了[1.23,7.213,-25.39]和[-30.10,100.2,42.42]作为亲本,则将对以下对分别进行交叉:
同样,当将突变算子应用于实数编码染色体时,它也分别应用于每个维度。
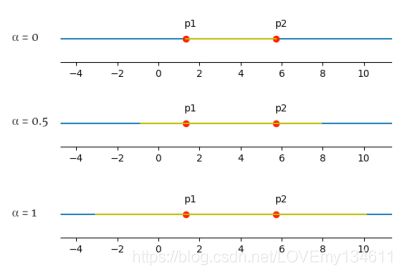
混合交叉(blend crossover)
在混合交叉中,每个后代都是从其父代创建的以下区间中随机选择的:
[ p a r e n t 1 − α ( p a r e n t 2 − p a r e n t 1 ) , p a r e n t 2 + α ( p a r e n t 2 − p a r e n t 1 ) ] [parent_1-α(parent_2-parent_1),parent_2+α(parent_2-parent_1)] [parent1−α(parent2−parent1),parent2+α(parent2−parent1)]
参数α是一个常数,其值在0到1之间。α值越大,区间就越大。
例如,如果双亲的值是1.33和5.72,则:
- α=0,将产生区间[1.33,5.72]
- α=0.5,将产生区间[-0.865,7.915]
- α=1.0,将产生区间[-3.06,10.11]
下图说明了这些示例,其中双亲分别用p1和p2标记,交叉间隔被标记为黄色:
模拟二进制交叉(simulated binary crossover)
模拟二进制交叉(simulated binary crossover,SBX)背后的想法是模仿二进制编码染色体通常使用的单点交叉的特性。其中特性之一是双亲平均值等于后代的平均值。
应用SBX时,两个后代是使用以下公式从双亲创建的:
o f f s p r i n g 1 = 1 2 [ ( 1 + β ) p a r e n t 1 + ( 1 − β ) p a r e n t 2 ] offspring_1=\frac 1 2 [(1+\beta)parent_1+(1-\beta)parent_2] offspring1=21[(1+β)parent1+(1−β)parent2]
o f f s p r i n g 2 = 1 2 [ ( 1 − β ) p a r e n t 1 + ( 1 + β ) p a r e n t 2 ] offspring_2=\frac 1 2 [(1-\beta)parent_1+(1+\beta)parent_2] offspring2=21[(1−β)parent1+(1+β)parent2]
其中β是被称为扩展因子的随机数。
该公式具有以下显着特性:
- 不管β的值如何,两个后代的平均值等于父母的平均值。
- 当β值为1时,后代是双亲的副本。
- 当β值小于1时,后代间的距离比亲代间的距离更短。
- 当β值大于1时,后代间的距离比双亲间的距离更远。
例如,如果双亲的值是1.33和5.72,则:
- β=0.8,产生后代1.769和5.281
- β=1.0,产生后代1.33和5.72
- β=1.2,产生后代0.891和6.159
下图说明了这些情况,其中双亲用p1和p2标记,后代用o1和o2标记:
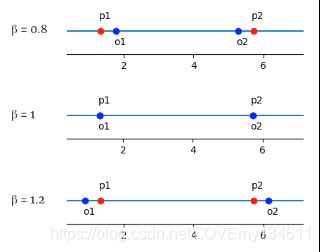
在上述每种情况下,两个后代的平均值为3.525,等于亲本的平均值。
二进制单点交叉的另一个属性是后代与父代之间的相似性。为此将β值的转化为随机分布。对于1左右的值,β的概率应该更高,因为后代与父母相似。为此,使用另一个以u表示的随机值计算β值,该值均匀分布在[0,1]上。选定u的值后,将按以下方式计算β:
f ( n ) = { β = ( 2 u ) 1 η + 1 , if n ≤ 0.5 β = [ 1 2 ( 1 − u ) ] 1 η + 1 , Otherwise f(n) = \begin{cases} \beta=(2u)^{\frac {1} {\eta + 1} }, & \text{if $n$ ≤ 0.5} \\ \beta=[\frac 1 {2(1-u)}]^{\frac {1} {\eta + 1} }, & \text{Otherwise} \end{cases} f(n)={ β=(2u)η+11,β=[2(1−u)1]η+11,if n ≤ 0.5Otherwise
其中η(eta)是代表分布指数的常数。当η值较大时,后代将更倾向于与其父母相似。 η的常用值为10或20。
实数突变
在实数编码的遗传算法中应用变异的一种选择是用随机产生的新值代替原有实数值。但是,这可能导致与原始个体没有任何关系的变异个体。
另一种方法是生成一个位于原始个体附近的随机实数。这种方法的一个例子是正态分布(或高斯)突变:使用均值为零和预定标准差的正态分布生成随机数,如下图所示: