【BI学习心得05-SVD矩阵分解与基于内容的推荐】
内容目录
-
- 写在前面的话
- 1.矩阵的几种分解方式
-
- 1.1共轭转置 Conjugate transpose
- 1.2Hermitian
- 1.3正定 positive definite
- 1.4正交矩阵 orthogonal matrix
- 1.5酉矩阵 unitary matrix
- 1.6正规矩阵 normal matrix
- 1.7类比
- 1.8分解
- 1.9Cholesky 分解
- 1.10QR分解
- 1.11特征分解/频谱分解 Eigendecomposition / spectral decomposition
- 1.12理论基础
- 1.13实对称矩阵
- 1.14正规矩阵
- 1.15奇异值分解
- 2.EVD矩阵
-
- 2.1为什么要做SVD?
- 2.2特征值分解EVD
- 2.3普通矩阵的矩阵分解
- 2.4用numpy计算特征值和特征向量
- 3.奇异值分解(SVD)原理详解
-
- 3.1正交变换
- 3.2特征值分解的含义
- 3.3SVD分解推导
- 3.4奇异值分解的原理小结
- 3.5奇异值分解的例子
- 3.6行降维和列降维
- 3.7SVD矩阵分解的应用场景
- 3.8 SVD总结
- 4.funkSVD, BiasSVD,SVD++算法
-
- 4.1原始SVD
-
- 4.1.1Surprise工具中的SVD
- 4.2FunkSVD
-
- 4.2.1Surprise工具中的FunkSVD
- 4.3BiasSVD
-
- 4.3.1Surprise工具中的BiasSVD
- 4.4SVD++
-
- 4.4.1Surprise工具中的SVD++
- 4.5funkSVD, BiasSVD,SVD++算法图像在上的应用
- 5.推荐系统中的NLP
-
- 5.1什么是 Word2vec?
- 5.2Skip-gram 和 CBOW 模型
-
- 5.2.1 Skip-gram 和 CBOW 的简单情形
- 5.2.2Skip-gram更一般的情形
- 5.2.3CBOW更一般的情形
- 5.3Word2vec的训练trick
- 5.4NLP推荐资料
- 参考资料
写在前面的话
随着人工智能的爆火,越来越多的人加入了这波学习人工智能的热潮。高校开设相关课程,但是拦在很多人面前的第一道难关不是编程,是数学。当然不例外的,要想深入理解并掌握SVD,我们需要弄清楚它的数学原理。通过数学原理不断扩充并延展出了SVD,以及相关变种。
1.矩阵的几种分解方式
1.1共轭转置 Conjugate transpose
如果我们有一个复数矩阵A:
[ 1 − 2 − i 5 1 + i i 4 − 2 i ] \begin{bmatrix} 1 & -2-i & 5\\ 1+i & i & 4-2i \end{bmatrix} \quad [11+i−2−ii54−2i]
A的转置为 A T A^T AT:
[ 1 1 + i − 2 − i i 5 4 − 2 i ] \begin{bmatrix} 1 & 1+i \\ -2-i & i\\ 5 & 4-2i\end{bmatrix} \quad ⎣⎡1−2−i51+ii4−2i⎦⎤
共轭转置为 A T ‾ \overline{A^T} AT
[ 1 1 − i − 2 + i − i 5 4 + 2 i ] \begin{bmatrix} 1 & 1-i \\ -2+i & -i\\ 5 & 4+2i\end{bmatrix} \quad ⎣⎡1−2+i51−i−i4+2i⎦⎤
共轭转置也经常记为: A ∗ A^* A∗, A H A^H AH(这个写法跟下面的 Hermitian 定义有关), A T ‾ \overline{A^T} AT
1.2Hermitian
Hermitian matrix 埃尔米特矩阵: 埃尔米特矩阵中每一个第i行第j列的元素都与第j行第i列的元素的复共轭。 也就是这个矩阵等于它的共轭转置。
我们知道复数 z = a + i b ∈ C z=a+ib\in C z=a+ib∈C,共轭复数 z = a − i b ∈ C z=a-ib\in C z=a−ib∈C
A H e r m i t i a n ⟺ a i j = a j i ‾ A H e r m i t i a n ⟺ A = A H ‾ \begin{aligned} A Hermitian \iff a_{ij}=\overline{a_{ji}}\\ A Hermitian \iff A=\overline{A^H} \end{aligned} AHermitian⟺aij=ajiAHermitian⟺A=AH
如果 A ∈ R n ∗ n A \in R^{n*n} A∈Rn∗n 是实数矩阵,并且是Hermitian,那么 a i j = a j i a_{ij}=a_{ji} aij=aji就是对称矩阵。实对称矩阵我们一般就说它是实对称矩阵,同时它也是Hermitian。
如果我们有一个复数矩阵A,那么它需要等于它的共轭转置,比如:
[ 2 2 + i 4 2 − i 3 i 4 − i 1 ] \begin{bmatrix} 2 & 2+i & 4\\ 2-i & 3 & i\\ 4 & -i & 1\end{bmatrix} \quad ⎣⎡22−i42+i3−i4i1⎦⎤
其实Hermitian也暗示了我们这个矩阵需要是方阵,至少我们转置之后的维度要跟原来的相等。
1.3正定 positive definite
一个 n ∗ n n*n n∗n的实对称矩阵M是正定的,当且仅当对于所有的非零实系数向量z,都有 z T M z > 0 z^TMz>0 zTMz>0。其中 z T z^T zT表示z的转置。
M p o s i t i v e d e f i n i t e ⟺ x M x > 0 f o r a l l x ∈ R n M \ positive \ definite \iff x^Mx>0 \ for \ all \ x\in R^n M positive definite⟺xMx>0 for all x∈Rn
首先,实对称矩阵 M 不一定是正定的,比如 M = -1:
[ 1 0 1 ] ∣ − 1 0 0 0 − 1 0 0 0 − 1 ∣ ∣ 1 0 1 ∣ = − 2 < 0 \begin{matrix} [ 1 & 0 & 1] \end{matrix} \begin{vmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -1 \end{vmatrix} \begin{vmatrix} 1 \\ 0 \\ 1 \end{vmatrix} = -2 < 0 [101]∣∣∣∣∣∣−1000−1000−1∣∣∣∣∣∣∣∣∣∣∣∣101∣∣∣∣∣∣=−2<0
对于复数,一个 n ∗ n n*n n∗n的埃尔米特矩阵M是正定的当且仅当对于每个非零的负向量z,都有 z ∗ M z z*Mz z∗Mz>0。其中 z ∗ z* z∗表示z的共轭转置。由于M是埃尔米特矩阵,经计算可知,对于任意的复向量z, z ∗ M z z*Mz z∗Mz必然是实数,从而可以与0比较大小。因此这个定义是自洽的。
M p o s i t i v e d e f i n i t e ⟺ x ∗ M x > 0 f o r a l l x ∈ C n M \ positive \ definite \iff x*Mx>0 \ for \ all \ x\in C^n M positive definite⟺x∗Mx>0 for all x∈Cn
Hermitian 也当然不一定正定,我们可以有一些判定方法:
- 矩阵M的所有的特征值 λ i \lambda_i λi 都是正的
1.4正交矩阵 orthogonal matrix
Q T = Q 1 ⟺ Q T Q = Q Q T = I Q^T=Q^{1} \iff Q^TQ=QQ^T=I QT=Q1⟺QTQ=QQT=I
1 = d e t ( I ) = d e t ( Q T Q ) = d e t ( Q T ) d e t ( Q ) = ( d e t ( Q ) ) 2 = > d e t ( Q ) = ± 1 1=det(I)=det(Q^TQ)=det(Q^T)det(Q)=(det(Q))^2=>det(Q)=±1 1=det(I)=det(QTQ)=det(QT)det(Q)=(det(Q))2=>det(Q)=±1
- 作为一个线性映射(变换矩阵),正交矩阵保持距离不变,所以它是一个保距映射,具体例子为旋转与镜射。
- 行列式值为+1的正交矩阵,称为特殊正交矩阵(special orthogonal group),它是一个旋转矩阵。
- 行列式值为-1的正交矩阵,称为瑕旋转矩阵。瑕旋转矩阵是旋转加上镜射。镜射也是一种瑕旋转。
- 所有 n ∗ n n*n n∗n的正交矩阵形成一个群 O ( n ) O(n) O(n),称为正交群。同样的,正交矩阵与正交矩阵的乘积也是一个正交矩阵。
- 所有特殊正交矩阵形成一个子群 S O ( n ) SO(n) SO(n),称为特殊正交群。同样的,旋转矩阵与旋转矩阵的乘积也是一个旋转矩阵。
1.5酉矩阵 unitary matrix
酉矩阵/幺正矩阵:
U U = U U = I n UU=UU=I_n UU=UU=In
就是 U 和其 共轭转置 U ∗ U^* U∗乘积为 单位矩阵。它是 正交矩阵 在复数上的推广。
酉(汉语拼音:yǒu)为地支的第十位,其前为申、其后为戌。酉月为农历八月,酉时为二十四小时制的17:00至19:00,在方向上指正西方。五行里酉代表金,阴阳学说里酉为阴。
说实话,这个字之前还没注意过它怎么念。unitary 作为 unit 的形容词,单位的、一元的,鉴于单位矩阵这个已经被 take 了,被翻成 幺正矩阵 也和不错,也大概有一元那么个意思。翻成酉矩阵大概也是文化人才能做到吧。
酉矩阵有很多很好的性质:
- U − 1 = U ∗ U^{-1}=U^* U−1=U∗,酉矩阵必定可逆,且逆矩阵等于其共轭转置
- ∣ λ n ∣ = 1 |\lambda_n|=1 ∣λn∣=1,酉矩阵U的所有特征值 λ n \lambda_n λn,其绝对值都是等于1的复数
- ∣ d e t ( U ) ∣ = 1 |det(U)|=1 ∣det(U)∣=1,酉矩阵U行列式的绝对值也是1
- ( U x ‾ ) ⋅ ( U y ‾ ) = x ‾ ⋅ y ‾ (U\overline{x})·(U\overline{y})=\overline{x}·\overline{y} (Ux)⋅(Uy)=x⋅y,酉矩阵U不会改变两个复向量 x ‾ \overline{x} x和 y ‾ \overline{y} y的点积
1.6正规矩阵 normal matrix
正规矩阵(英语:normal matrix)A 是与自己的共轭转置满足交换律的复系数方块矩阵,也就是说,A 满足
A ∗ A = A A ∗ A^*A=AA^* A∗A=AA∗
A ∗ A^* A∗是A的共轭转置。
如果A是实系数矩阵,则 A ∗ = A T A^*=A^T A∗=AT,从而条件简化为 A A T = A T A AA^T=A^TA AAT=ATA。
正规矩阵的概念十分重要,因为它们正是能使谱定理成立的对象:矩阵 A 正规当且仅当它可以被成 A = U Λ U ∗ A=U\Lambda U^* A=UΛU∗的形式。其中的 Λ = d i a g ( λ 1 , λ 2 , … ) \Lambda = diag(\lambda_1, \lambda_2, \dots) Λ=diag(λ1,λ2,…)为对角矩阵,U 为酉矩阵。
总而言之,就是正规矩阵一定可以特征分解/频谱分解/谱定理。
1.7类比
不同种类的正规矩阵可以与各种复数建立对应的类比关系。比如:
- 可逆矩阵类似于非零的复数。
- 矩阵的共轭转置类似于复数的共轭
- 酉矩阵类似于模等于1的复数。
- 埃尔米特矩阵类似于实数。
- 埃尔米特矩阵中的正定矩阵类似于正实数。
1.8分解
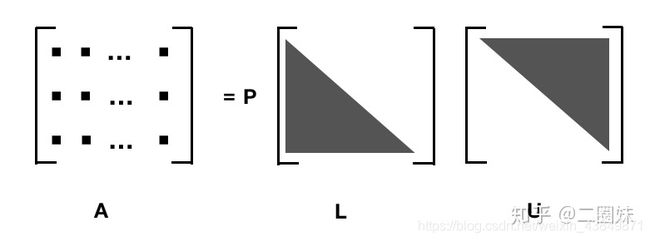
A = P L U A=PLU A=PLU
- 适用:方阵
- 分解: A = PLU, L 是 下三角阵, U 是 上三角阵,而 P 则是 permutation 行变换,单位矩阵变换可得, 如果没有行变换,A 就 直接分解成 LU. PLU 分解源自高斯消元法。
1.9Cholesky 分解
- 适用:方阵、hermitian、正定 positive definite
- 分解: A=LL^*
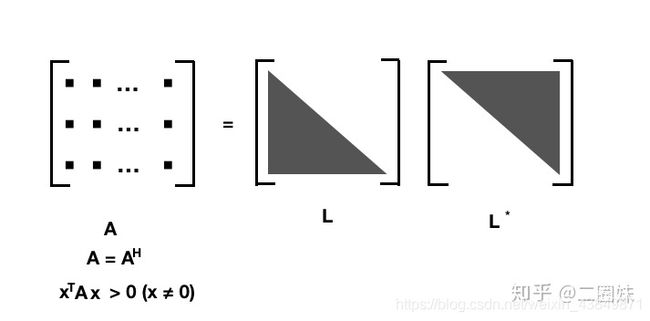
A 是正定的 Hermitian阵, L 是下三角矩阵, L ∗ L^* L∗是 L 的共轭转置, 是一个上三角。
1.10QR分解
- 适用于:列向量线性无关的矩阵m*n, m ≥ n m\ge n m≥n
- 分解:A=QR,Q是 m ∗ n m*n m∗n的酉矩阵,又叫做幺正矩阵(unitary matrix), R 是一个上三角矩阵
对于方阵的QR分解我比较熟悉
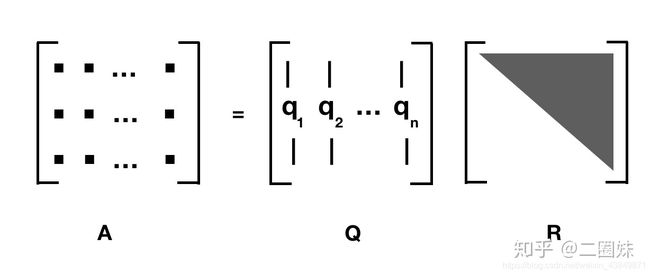
如果A不是方阵的话,那么三角矩阵只会占据一部分,下面会都是0, 所以经常也这样写 QR 分解:
A = Q R = Q ∣ R 1 0 ∣ = [ Q 1 , Q 2 ] ∣ R 1 0 ∣ = Q 1 R 1 A=QR=Q\begin{vmatrix}R_1 \\ 0 \end{vmatrix} =\begin{matrix}[Q_1,Q_2 ]\end{matrix}\begin{vmatrix}R_1 \\ 0 \end{vmatrix}=Q_1R_1 A=QR=Q∣∣∣∣R10∣∣∣∣=[Q1,Q2]∣∣∣∣R10∣∣∣∣=Q1R1
where R1 is an n×n upper triangular matrix, 0 is an (m − n)×n zero matrix, Q1 is m×n, Q2 is m×(m − n), and Q1 and Q2 both have orthogonal columns.
计算 QR 分解 我们可以用 Gram–Schmidt 或者 Householder reflections.
1.11特征分解/频谱分解 Eigendecomposition / spectral decomposition
- 适用于: 具有线性独立特征向量(不一定是不同特征值)的方阵 A
- 分解: A = Q Λ Q − 1 A=Q\Lambda Q^{-1} A=QΛQ−1
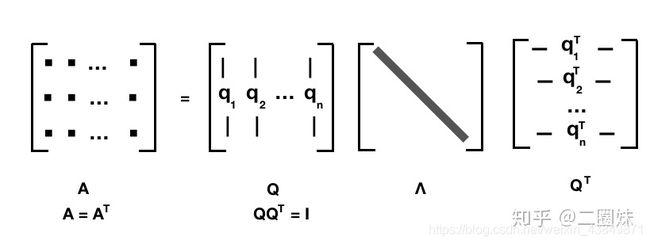
Q 是 n x n 的矩阵, 第 i 列是 A 的 特征向量 q i ‾ , Λ \overline{q_i},\Lambda qi,Λ是对角阵,其中第 i个 对角元素 Λ i i = λ i \Lambda_{ii}=\lambda_i Λii=λi, 是跟 特征向量 q i ‾ \overline{q_i} qi对应的 特征值 λ i \lambda_i λi. 这里需要注意只有可对角化矩阵才可以作特征分解。比如 ∣ 1 1 0 1 ∣ \begin{vmatrix}1 & 1 \\ 0 & 1\end{vmatrix} ∣∣∣∣1011∣∣∣∣不能被对角化,也就不能特征分解。
一般来说,特征向量 q i ‾ , ( i = 1 , . . . , N ) \overline{q_i},(i=1,...,N) qi,(i=1,...,N)一般被单位化(但这不是必须的)。未被单位化的特征向量组 q i ‾ , ( i = 1 , . . . , N ) \overline{q_i},(i=1,...,N) qi,(i=1,...,N)也可以作为Q的列向量。这一事实可以这样理解:Q中向量的长度都被Q^1抵消了。
这里我们虽然用了Q这个字母,但是我们并没有说它是一个正交阵,因为之前写特征分解的手也提到过:
对于任意矩阵,其对应于不同特征值的特征向量线性无关,但不一定正交,而对于实对称矩阵,其对应于不同特征值的特征向量是相互正交的。
特征分解很容易推导:
A v = λ v A Q = Q Λ A = Q Λ Q − 1 . {\displaystyle {\begin{aligned}\mathbf {A} \mathbf {v} &=\lambda \mathbf {v} \\\mathbf {A} \mathbf {Q} &=\mathbf {Q} \mathbf {\Lambda } \\\mathbf {A} &=\mathbf {Q} \mathbf {\Lambda } \mathbf {Q} ^{-1}.\end{aligned}}} AvAQA=λv=QΛ=QΛQ−1.
1.12理论基础
A v ⃗ = λ v ⃗ p ( λ ) = d e t ( A − λ I ) = 0 A\vec{v} = \lambda \vec{v} \\ p(\lambda) = det(A - \lambda I) = 0 Av=λvp(λ)=det(A−λI)=0
由代数基本定理(Fundamental theorem of algebra)我们知道 [公式] 有 N 个解。这些解的解集也就是特征值的集合,有时也称为“谱”(Spectrum)。
代数基本定理: 任何一个非零的一元n次复系数多项式,都正好有n个复数根(重根视为多个根)。
因式分解:
p ( λ ) = ( λ − λ 1 ) n 1 ( λ − λ 2 ) n 2 . . . ( λ − λ k ) n k = 0 p(\lambda)=(\lambda-\lambda_1)^{n1}(\lambda-\lambda_2)^{n2}...(\lambda-\lambda_k)^{nk}=0 p(λ)=(λ−λ1)n1(λ−λ2)n2...(λ−λk)nk=0
其中:
∑ i = 1 k n i = N \sum^k_{i=1}n_i=N i=1∑kni=N
对每一个特征值 λ i \lambda_i λi,我们都有下式成立:
( A − λ i I ) v = 0 (A-\lambda_iI)v=0 (A−λiI)v=0
对每一个特征方程,都会有 m i ( 1 ≤ m i ≤ n i ) m_i(1\le m_i \le n_i) mi(1≤mi≤ni)个线性无关的解。这 m i m_i mi个向量与一个特征值 λ i \lambda_i λi相对应。这里,整数 [公式] 称为特征值 [公式] 的几何重数(geometric multiplicity),而 n i n_i ni称为代数重数(algebraic multiplicity)。这里需要注意的是几何重数与代数重数可以相等,但也可以不相等。一种最简单的情况是 m i = n i = 1 m_i=n_i=1 mi=ni=1。特征向量的极大线性无关向量组中向量的个数可以由所有特征值的几何重数之和来确定。
这也是之前我们强调适用条件是 “具有线性独立特征向量(不一定是不同特征值)的方阵 A”,也就是看 n x n 的方阵 A 是否可以特征分解主要是看几何重数之和是否为 n 了。
1.13实对称矩阵
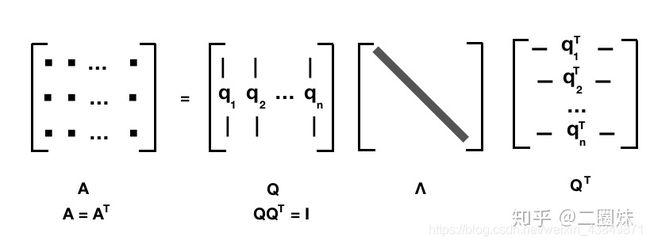
对于任意的 n x n 实对称矩阵都有 n 个线性无关的特征向量,并且这些特征向量都可以正交单位化而得到一组正交且模为 1 的向量。所以:
A = Q Λ Q T \mathbf{A}=\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{T} A=QΛQT
1.14正规矩阵
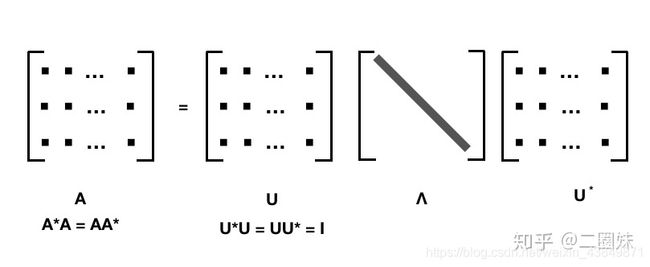
一个复正规矩阵具有一组正交特征向量基,故正规矩阵可以被分解成
A = U Λ U ∗ \mathbf{A}=\mathbf{U}\mathbf{\Lambda}\mathbf{U}^{*} A=UΛU∗
特征分解对于理解线性常微分方程或线性差分方程组的解很有用。 例如,差分方程 x t + 1 = A x t x_t+1=Ax_t xt+1=Axt初始条件开始 x 0 = c x_0=c x0=c到 x t = A t c x_t=A^tc xt=Atc,相当于 x t = V D t V − 1 c x_t=VD^tV^{-1}c xt=VDtV−1c,其中V和D是由A的特征向量和特征值形成的矩阵。 由于D是对角线,D 的 t 次幂 D t D^t Dt只是涉及将对角线上的每个元素的 t 次幂 。 这与 A 的 t的次幂相比 ,更容易实现和理解,因为A通常不是对角线。
这里就直接点出了一个特征分解的应用场景。解线性方程常微分方程或线性差分方程组。
1.15奇异值分解
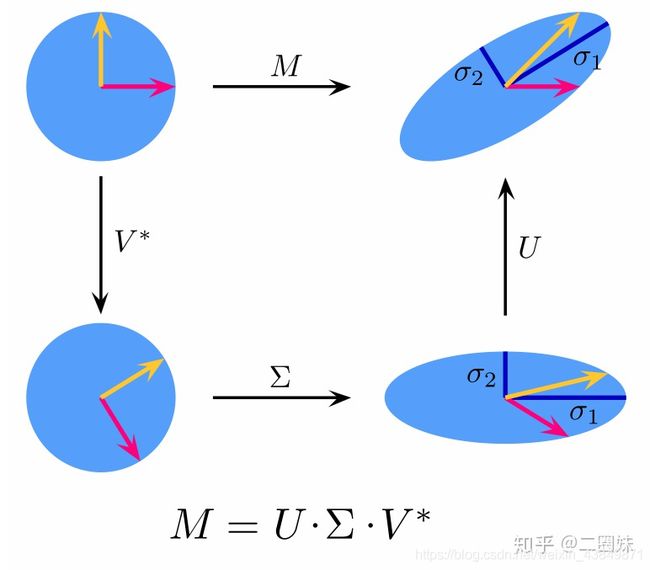
- 适用于: m x n 矩阵A
- 分解: A = U ∑ V ∗ A=U\sum V^* A=U∑V∗,U和V都是酉矩阵/幺正矩阵,也就是满足 U ∗ U = V ∗ V = I U^*U=V^*V=I U∗U=V∗V=I, ∑ \sum ∑是对角阵,对角上的元素称为A的奇异值,U和V并不一定是唯一的。
2.EVD矩阵
矩阵分解模型在推荐系统中有非常不错的表现,相对于传统的协同过滤方法,它不仅能通过降维增加模型的泛化能力,也方便加入其他因素(如数据偏差、时间、隐反馈等)对问题建模,从而产生更佳的推荐结果。
先来说说矩阵分解几个明显的特点,它具有协同过滤的 “集体智慧”,隐语义的 “深层关系”,以及机器学习的 “以目标为导向的有监督学习”。在了解了基于邻域的协同过滤算法后,集体智慧自不必多说,我们依次从 “隐因子” 和 “有监督学习” 的角度来了解矩阵分解的基本思路。
基于矩阵分解的推荐算法的核心假设是用隐语义(隐变量)来表达用户和物品,他们的乘积关系就成为了原始的元素。这种假设之所以成立,是因为我们认为实际的交互数据是由一系列的隐变量的影响下产生的(通常隐变量带有统计分布的假设,就是隐变量之间,或者隐变量和显式变量之间的关系,我们往往认为是由某种分布产生的。),这些隐变量代表了用户和物品一部分共有的特征,在物品身上表现为属性特征,在用户身上表现为偏好特征,只不过这些因子并不具有实际意义,也不一定具有非常好的可解释性,每一个维度也没有确定的标签名字,所以才会叫做 “隐变量”。而矩阵分解后得到的两个包含隐变量的小矩阵,一个代表用户的隐含特征,一个代表物品的隐含特征,矩阵的元素值代表着相应用户或物品对各项隐因子的符合程度,有正面的也有负面的。
随着人们的不断探索和研究,衍生出了矩阵分解的一系列算法,接下来的时间,分别讲讲矩阵分解的几种方法。
2.1为什么要做SVD?
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们也可以用最大的K个的奇异值和对应的左右奇异向量来近似描述矩阵。其中K要比n小很多,也就是一个大的矩阵A可以用三个小的矩阵来表示。数学之美中有说,会减少很大的存储资源。
K怎么确定?
多启发式的算法,当然,最直接的是直接用肉眼观察。除此之外,一个典型做法是保留矩阵中90%的能量信息。具体来讲,我们可以对奇异值求平方和。于是可以对奇异值的平方和累加直至总和的90%为止。
2.2特征值分解EVD
在讨论SVD之前先讨论矩阵的特征值分解(EVD)(eigenvalue decomposition),对称阵有一个很优美的性质:它总能相似对角化,对称阵特征值对应的特征向量两两正交。
A = V ∗ D ∗ V T A=V*D*V^T A=V∗D∗VT
其中A的对称矩阵,D是对角矩阵,对角元素是A的特征值(几何意义:变换时的缩放),V的列是A的特征向量(几何意义:特征向量经过矩阵A的变换,只进行缩放(特征值的大小),不改变其方向),特征向量两两正交,可以理解为一个高维的空间。
我们看看上面的公式怎么得来的:
设特征值为 λ \lambda λ,单位特征向量为x,那么所有的特征值和单位特征向量有: A v = λ v Av=\lambda v Av=λv
λ为特征值(标量),v为特征值 λ对应的特征向量。特征向量被施以线性变换 A 只会使向量伸长或缩短,而方向保持不变
2.3普通矩阵的矩阵分解
我们在学线性代数的时候,都会学到怎么求解特征值和特征向量。通常把|A-λI|=0,这个式子也称为特征方程。
- 令p(λ):=|A-λI|称为矩阵的特征多项式
- 特征多项式是关于 的N次多项式,特征方程有N个解
- 对多项式 p ( λ ) p(\lambda) p(λ)进行因式分解,可得 p ( λ ) = ( λ − λ 1 ) n 1 ( λ − λ 2 ) n 2 . . . ( λ − λ k ) n k = 0 p(\lambda)=(\lambda-\lambda_1)^{n_1}(\lambda-\lambda_2)^{n_2}...(\lambda-\lambda_k)^{n_k}=0 p(λ)=(λ−λ1)n1(λ−λ2)n2...(λ−λk)nk=0,其中 ∑ i = 1 k n i = N \sum_{i=1}^kn_i=N ∑i=1kni=N,而对于每一个特征值 λ i \lambda_i λi,都可以使得 ( A − λ i I ) v = 0 (A-\lambda_iI)v=0 (A−λiI)v=0
- 计算矩阵A的特征值和特征向量:
A = [ 4 2 − 5 6 4 − 9 5 3 − 7 ] A=\begin{bmatrix} 4 & 2 & -5 \\ 6 & 4 & -9 \\ 5 & 3 & -7 \\ \end{bmatrix} A=⎣⎡465243−5−9−7⎦⎤ - 求解特征方程 ∣ λ I − A ∣ = [ λ − 4 − 2 5 − 6 λ − 4 9 − 5 − 3 λ + 7 ] = 0 |\lambda I -A|=\begin{bmatrix} \lambda-4 & -2 & 5 \\ -6 & \lambda-4 & 9 \\ -5 & -3 & \lambda+7\\ \end{bmatrix}=0 ∣λI−A∣=⎣⎡λ−4−6−5−2λ−4−359λ+7⎦⎤=0
p ( λ ) : = ∣ λ I − A ∣ = λ 2 ∗ ( λ − 1 ) p(\lambda):=|\lambda I -A|=\lambda^2*(\lambda - 1) p(λ):=∣λI−A∣=λ2∗(λ−1), λ 2 ∗ ( λ − 1 ) = 0 \lambda^2*(\lambda - 1)=0 λ2∗(λ−1)=0求解得 λ 1 = 1 \lambda_1=1 λ1=1, λ 2 = λ 3 = 0 \lambda_2=\lambda_3=0 λ2=λ3=0
当 λ 1 = 1 \lambda_1=1 λ1=1, ∣ λ 1 I − A ∣ = [ − 3 − 2 5 − 6 − 3 9 − 5 − 3 8 ] |\lambda_1 I -A|=\begin{bmatrix} -3 & -2 & 5 \\ -6 & -3 & 9 \\ -5 & -3 & 8\\ \end{bmatrix} ∣λ1I−A∣=⎣⎡−3−6−5−2−3−3598⎦⎤
简化得到 [ 1 0 − 1 0 1 − 1 0 0 0 ] \begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0\\ \end{bmatrix} ⎣⎡100010−1−10⎦⎤
所以 ( E − A ) x = [ 1 0 − 1 0 1 − 1 0 0 0 ] [ x 1 x 2 x 3 ] = 0 (E-A)x=\begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0\\ \end{bmatrix}\begin{bmatrix} x_1\\ x_2 \\ x_3\\ \end{bmatrix}=0 (E−A)x=⎣⎡100010−1−10⎦⎤⎣⎡x1x2x3⎦⎤=0
即 f ( x ) = { x 1 − x 3 = 0 x 2 − x 3 = 0 f(x)= \begin{cases} x_1-x_3=0\\ x_2-x_3=0\\ \end{cases} f(x)={ x1−x3=0x2−x3=0,令 x 1 = 1 x_1=1 x1=1,得到特征矩阵 ζ 1 = [ 1 1 1 ] \zeta_1=\begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix} ζ1=⎣⎡111⎦⎤
同理,当 λ 2 = λ 3 = 0 \lambda_2=\lambda_3=0 λ2=λ3=0,计算可得特征矩阵 ζ 2 = ζ 3 = [ 1 3 2 ] \zeta_2=\zeta_3=\begin{bmatrix}1 \\ 3 \\ 2\end{bmatrix} ζ2=ζ3=⎣⎡132⎦⎤
A是MxN维的方阵,对矩阵A进行特征分解: A = U Σ U − 1 A=U\Sigma U^{-1} A=UΣU−1
- U U U是列向量是A的特征向量
- Σ \Sigma Σ是对角矩阵,元素是特征向量的特征值

特征值5.64575131对应的特征向量为[0.97760877 0.21043072]
特征值0.35424869对应的特征向量为[-0.54247681 0.84007078]
结论:特征向量之间一定线性无关
如果A 是对称方阵,那么 U T = u − 1 A = U Σ U T U^T = u^{-1}\\ A=U\Sigma U^T UT=u−1A=UΣUT
- U U U是列向量是A的特征向量
- Σ \Sigma Σ是对角矩阵,元素是特征向量的特征值

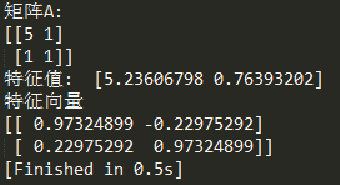
特征值5.23606798对应的特征向量为[0.97324899 0.22975292]
特征值0.76393202对应的特征向量为[-0.22975292 0.97324899]
结论:不仅线性无关,而且还正交,即
0.97324899*-0.22975292+0.22975292*0.97324899=0
2.4用numpy计算特征值和特征向量
import numpy as np
A = np.array([[5,3],
[1,1]])
lamda, U = np.linalg.eig(A)
print('矩阵A: ')
print(A)
print('特征值: ',lamda)
print('特征向量')
print(U)
3.奇异值分解(SVD)原理详解
3.1正交变换
正交变换公式:
X = U Y X=UY X=UY
上式表示:X是Y的正交变换,其中U是正交矩阵,X和Y为列向量。下面用一个例子说明正交变换的含义:
假设有两个单位列向量a和b,两向量的夹角为θ,如下图所示:
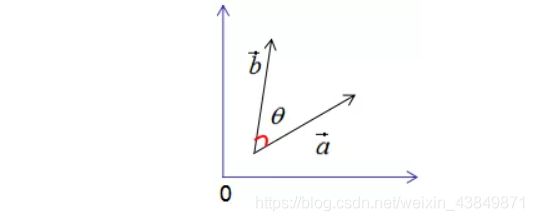
现对向量a,b进行正交变换:
a ⃗ = U ∗ a ⃗ b ⃗ = U ∗ b ⃗ \vec{a}=U*\vec{a}\\ \vec{b}=U*\vec{b} a=U∗ab=U∗b
a ⃗ , b ⃗ \vec{a},\vec{b} a,b的模:
∣ ∣ a ⃗ ∣ ∣ = ∣ ∣ U ∗ a ⃗ ∣ ∣ = ∣ ∣ U ∣ ∣ ∗ ∣ ∣ a ⃗ ∣ ∣ = ∣ ∣ a ⃗ ∣ ∣ = 1 ∣ ∣ b ⃗ ∣ ∣ = ∣ ∣ U ∗ b ⃗ ∣ ∣ = ∣ ∣ U ∣ ∣ ∗ ∣ ∣ b ⃗ ∣ ∣ = ∣ ∣ b ⃗ ∣ ∣ = 1 ||\vec{a}||=||U*\vec{a}||=||U||*||\vec{a}||=||\vec{a}||=1\\ ||\vec{b}||=||U*\vec{b}||=||U||*||\vec{b}||=||\vec{b}||=1\\ ∣∣a∣∣=∣∣U∗a∣∣=∣∣U∣∣∗∣∣a∣∣=∣∣a∣∣=1∣∣b∣∣=∣∣U∗b∣∣=∣∣U∣∣∗∣∣b∣∣=∣∣b∣∣=1
有上式可知 a ⃗ , b ⃗ \vec{a},\vec{b} a,b的模都为1。
a ⃗ 和 b ⃗ \vec{a}和\vec{b} a和b的內积:
a ⃗ T ∗ b ⃗ = ( U ∗ a ⃗ ) T ∗ ( U ∗ b ⃗ ) = a ⃗ T U T U b ⃗ ⇒ a ⃗ T ∗ b ⃗ = a ⃗ T ∗ b ⃗ ( 1 ) \vec{a}^T*\vec{b}=(U*\vec{a})^T*(U*\vec{b})=\vec{a}^TU^TU\vec{b}\\ \Rightarrow\vec{a}^T*\vec{b}=\vec{a}^T*\vec{b}(1) aT∗b=(U∗a)T∗(U∗b)=aTUTUb⇒aT∗b=aT∗b(1)
由上式可知,正交变换前后的內积相等。
a ⃗ 和 b ⃗ \vec{a}和\vec{b} a和b的夹角 θ ′ θ^{' } θ′:
c o s θ ′ = a ⃗ T ∗ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∗ ∣ ∣ b ⃗ ∣ ∣ ( 2 ) c o s θ = a ⃗ T ∗ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∗ ∣ ∣ b ⃗ ∣ ∣ ( 3 ) cosθ^{' }=\frac{\vec{a}^T*\vec{b}}{||\vec{a}||*||\vec{b}||}(2)\\ cosθ=\frac{\vec{a}^T*\vec{b}}{||\vec{a}||*||\vec{b}||}(3)\\ cosθ′=∣∣a∣∣∗∣∣b∣∣aT∗b(2)cosθ=∣∣a∣∣∗∣∣b∣∣aT∗b(3)
比较(2)式和(3)式可得:正交变换前后的夹角相等,即 θ = θ ′ θ=θ^{' } θ=θ′。因此,正交变换的性质可用下图来表示:
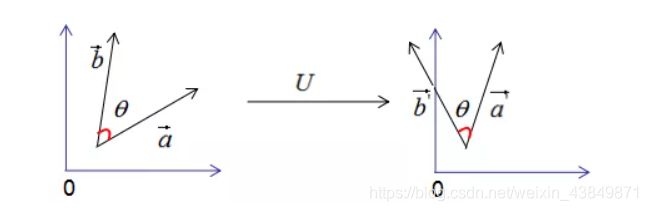
正交变换的两个重要性质:
- 正交变换不改变向量的模;
- 正交变换不改变向量的夹角;
如果向量 a ⃗ 和 b ⃗ \vec{a}和\vec{b} a和b是基向量,那么正交变换的结果如下图所示:
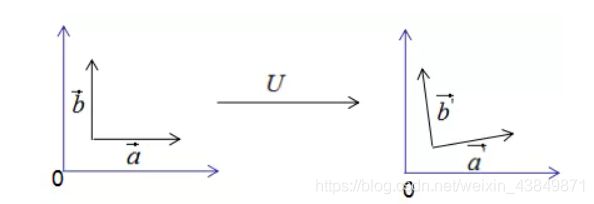
上图可以得到重要结论: 基 向 量 正 交 变 换 后 的 结 果 仍 是 基 向 量 \color{red}基向量正交变换后的结果仍是基向量 基向量正交变换后的结果仍是基向量。基向量是表示向量最简洁的办法,向量在基向量的投影就是基向量的坐标,我们通过这种思想去理解特征值分解和推导SVD分解。
3.2特征值分解的含义
对称方阵A的特征值分解为:
A = U Σ U − 1 ( 2.1 ) A=U\Sigma U^{-1}(2.1) A=UΣU−1(2.1)
其中U是正交矩阵, Σ \Sigma Σ是对角矩阵。
为了可视化特征值分解,假设A是2x2的对称矩阵, U = ( u 1 , u 2 ) U=(u1,u2) U=(u1,u2), Σ = ( λ 1 , λ 2 ) \Sigma=(λ1,λ2) Σ=(λ1,λ2)。(2.1)式展开为:
A u 1 = λ 1 u 1 A u 2 = λ 2 u 2 Au_1=λ_1u_1 \\ Au_2=λ_2u_2 Au1=λ1u1Au2=λ2u2
用图形表示为:
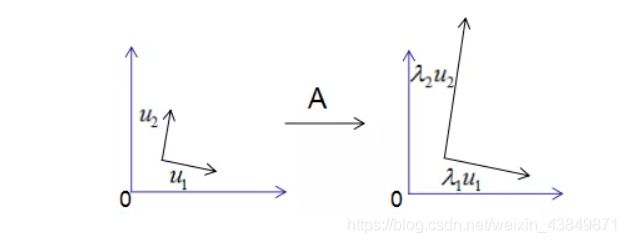
由 上 图 可 知 , 矩 阵 A 没 有 旋 转 特 征 向 量 , 它 只 是 对 特 征 向 量 进 行 了 拉 伸 或 缩 短 ( 取 决 于 特 征 值 的 大 小 ) , 因 此 , 对 称 矩 阵 对 其 特 征 向 量 ( 基 向 量 ) 的 变 换 仍 然 是 基 向 量 ( 单 位 化 ) \color{red}由上图可知,矩阵A没有旋转特征向量,它只是对特征向量进行了拉伸或\\ 缩短(取决于特征值的大小),因此,对称矩阵对其特征向量(基向量)的变换\\ 仍然是基向量(单位化) 由上图可知,矩阵A没有旋转特征向量,它只是对特征向量进行了拉伸或缩短(取决于特征值的大小),因此,对称矩阵对其特征向量(基向量)的变换仍然是基向量(单位化)。
特征向量和特征值的几何意义:若向量经过矩阵变换后保持方向不变,只是进行长度上的伸缩,那么该向量是矩阵的特征向量,伸缩倍数是特征值。
3.3SVD分解推导
我们考虑了当基向量是对称矩阵的特征向量时,矩阵变换后仍是基向量, 但 是 , 我 们 在 实 际 项 目 中 遇 到 的 大 都 是 行 和 列 不 相 等 的 矩 阵 \color{red}但是,我们在实际项目中遇到的大都是行和列不相等的矩阵 但是,我们在实际项目中遇到的大都是行和列不相等的矩阵,如统计每个学生的科目乘积,行数为学生个数,列数为科目数,这种形成的矩阵很难是方阵, 因 此 S V D 分 解 是 更 普 遍 的 矩 阵 分 解 方 法 \color{red}因此SVD分解是更普遍的矩阵分解方法 因此SVD分解是更普遍的矩阵分解方法 。
先回顾一下正交变换的思想来推导SVD分解:假设A是M*N的矩阵,秩为K,Rank(A)=k。
存在一组正交基V:
V = ( v 1 , v 2 , . . . , v k ) V=(v_1,v_2,...,v_k) V=(v1,v2,...,vk)
矩阵对其变换后仍是正交基,记为U:
U = ( A v 1 , A v 2 , . . . , A v k ) U=(Av_1,Av_2,...,Av_k) U=(Av1,Av2,...,Avk)
由正交基定义,得:
( A v i ) T ( A v i ) = 0 ( 3.1 ) (Av_i)^T(Av_i)=0(3.1) (Avi)T(Avi)=0(3.1)
上式展开:
v i T A T v j = 0 ( 3.2 ) v_{i}^TA^Tv_j=0(3.2) viTATvj=0(3.2)
当v_t是A^TA的特征向量时,有:
( A T A ) v i = λ v i (A^TA)v_i=λv_i (ATA)vi=λvi
所以,(3.2)式得:
λ v i T v j = 0 λv_i^{T}v_j=0 λviTvj=0
即假设成立。
图形表示如下:
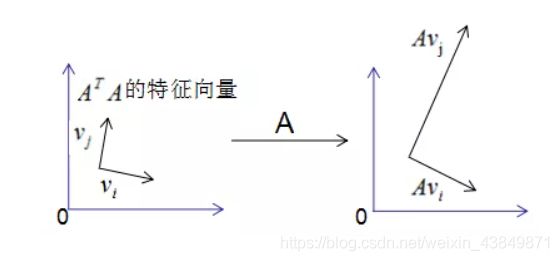
正交向量的模:
∣ ∣ A v i ∣ ∣ 2 = ( A v i ) T ∗ ( A v i ) ⇒ ∣ ∣ A v i ∣ ∣ 2 = v i T ∗ A T A v ⇒ ∣ ∣ A v i ∣ ∣ 2 = λ i v i T v = λ i ∴ ∣ ∣ A v i ∣ ∣ = λ i ||Av_i||^2=(Av_i)^T*(Av_i) \\ \Rightarrow ||Av_i||^2=v_i^T*A^TAv \\ \Rightarrow ||Av_i||^2=λ_iv_i^Tv=λ_i \\ \therefore ||Av_i||=\sqrt{λ_i} ∣∣Avi∣∣2=(Avi)T∗(Avi)⇒∣∣Avi∣∣2=viT∗ATAv⇒∣∣Avi∣∣2=λiviTv=λi∴∣∣Avi∣∣=λi
单位化正交向量,得到:
u i = A v i ∣ ∣ A v i ∣ ∣ = 1 λ i = A v i ⇒ A v i = λ i ∗ u i ( 3.3 ) u_i=\frac{Av_i}{||Av_i||}=\frac{1}{\sqrt{λ_i}}=Av_i \\ \Rightarrow Av_i=\sqrt{λ_i}*u_i (3.3) ui=∣∣Avi∣∣Avi=λi1=Avi⇒Avi=λi∗ui(3.3)
用矩阵的形式表示(3.3)式:
A V = U Σ ( 3.4 ) AV=U\Sigma(3.4) AV=UΣ(3.4)
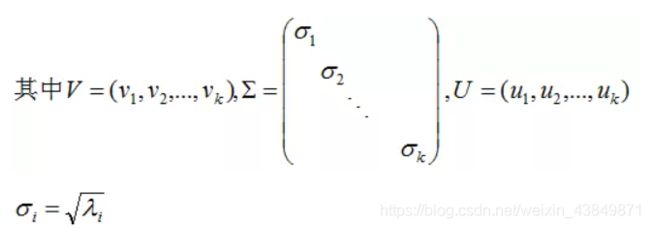
V是NK矩阵,U是MK矩阵, ∑ \sum ∑是MK的矩阵,需要扩展成方阵形式:
将正交基 U = ( u 1 , u 2 , . . . , u k ) U=(u_1,u_2,...,u_k) U=(u1,u2,...,uk)扩展 ( u 1 , u 2 , . . . , u m ) R m (u_1,u_2,...,u_m)R^m (u1,u2,...,um)Rm空间的正交基,即U是MM方阵。将正交基 V = ( v 1 , v 2 , . . . , v k ) V=(v_1,v_2,...,v_k) V=(v1,v2,...,vk)扩展成 ( v 1 , v 2 , . . . , v n ) R n (v_1,v_2,...,v_n)R^n (v1,v2,...,vn)Rn空间的正交基,其中 ( v k + 1 , v k + 2 , . . . , v n ) (v_{k+1},v_{k+2},...,v_n) (vk+1,vk+2,...,vn)是矩阵A的零空间,即:
A v i = 0 , i > k Av_i=0,i>k Avi=0,i>k
对应的特征值 σ i = 0 \sigma_i=0 σi=0, Σ \Sigma Σ是MN对角矩阵,V是NN方阵,因此(3.4)式写成向量形式为:
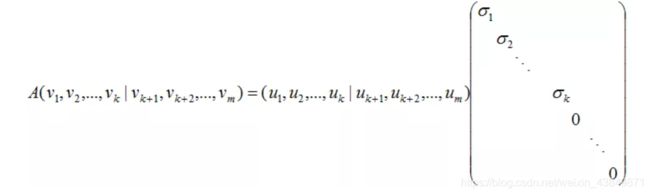
得出:
A V = U Σ AV=U\Sigma AV=UΣ
两式右乘 V T V^T VT,可得矩阵的奇异值分解:
A = U Σ V T ( 3.5 ) A=U\Sigma V^T(3.5) A=UΣVT(3.5)
(3.5)式写成向量形式:

令
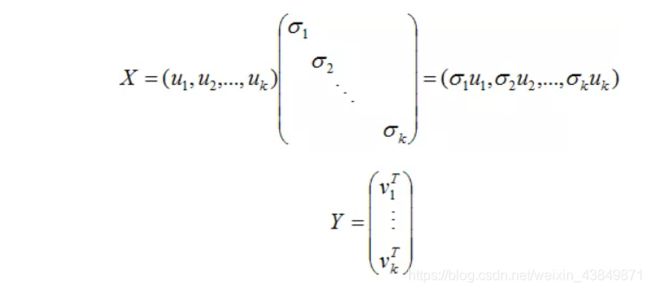
则: A = X Y A=XY A=XY
因为X和Y分别是列满秩和行满秩,所以上式是A的满秩分解。
(3.5)式的奇异矩阵 ∑ \sum ∑的值 σ \sigma σ是 A T A A^TA ATA特征值的平方根,下面推导奇异值分解的U和V:
A T A = ( U Σ V T ) T ( U Σ V T ) = V Σ U T ∗ V Σ U T = U Σ 2 U T \begin{array}{lcl} A^TA &=& (U\Sigma V^T)^T(U\Sigma V^T) \\ &=& V\Sigma U^T *V\Sigma U^T\\ &=& U\Sigma^2 U^T \end{array} ATA===(UΣVT)T(UΣVT)VΣUT∗VΣUTUΣ2UT
即U是 A A T AA^T AAT的特征向量构成的矩阵,称为左奇异矩阵。
3.4奇异值分解的原理小结
矩阵A的奇异值分解是 A = U Σ V T A=U\Sigma V^T A=UΣVT,其中U是 A A T AA^T AAT的特征向量构成的矩阵,V是 A A T AA^T AAT的特征向量构成的矩阵,奇异值矩阵 Σ \Sigma Σ的值是 A T A A^TA ATA特征值的平方根。
3.5奇异值分解的例子
接下来我们用一个简单的例子来说明矩阵是如何进行奇异值分解的。矩阵A定义为: ( 1 1 1 1 1 0 ) \begin{pmatrix} 1 & 1 \\ 1 & 1 \\ 1 & 0 \end{pmatrix} ⎝⎛111110⎠⎞
首先求出 A T A 和 A A T A^TA和AA^T ATA和AAT:
A T A = ( 1 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 2 1 1 2 ) A^TA=\begin{pmatrix} 1 & 1 & 1\\ 1 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{pmatrix} =\begin{pmatrix} 2 & 1 \\ 1 & 2 \\ \end{pmatrix} ATA=(111110)⎝⎛011110⎠⎞=(2112)
A A T = ( 0 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 1 1 0 1 2 1 0 1 1 ) AA^T=\begin{pmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 & 1\\ 1 & 1 & 0\\ \end{pmatrix} =\begin{pmatrix} 1 & 1 & 0\\ 1 & 2 & 1\\ 0 & 1 & 1 \end{pmatrix} AAT=⎝⎛011110⎠⎞(011110)=⎝⎛110121011⎠⎞
接下来,求 A A T AA^T AAT的特征向量V和特征值 λ \lambda λ:
( 1 2 − 1 2 1 2 1 2 ) \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} (2121−2121),对应的特征值: λ 1 = 3 , λ 2 = 1 \lambda_1=3,\lambda_2=1 λ1=3,λ2=1
奇异值是特征值的平方根: σ 1 = 3 , σ 2 = 1 \sigma_1=3,\sigma_2=1 σ1=3,σ2=1
再求 A A T AA^T AAT的特征向量U:
U = ( 1 6 1 2 1 3 2 6 0 1 2 1 6 − 1 2 1 3 ) U=\begin{pmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}}\\ \frac{2}{\sqrt{6}} & 0 &\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}}\\ \end{pmatrix} U=⎝⎜⎛616261210−21312131⎠⎟⎞
最后得到A矩阵的奇异值分解:
A = U Σ V T ( 1 6 1 2 1 3 2 6 0 1 2 1 6 − 1 2 1 3 ) ( 3 0 0 1 0 0 ) ( 1 2 1 2 − 1 2 1 2 ) A= U\Sigma V^T \begin{pmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}}\\ \frac{2}{\sqrt{6}} & 0 &\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}}\\ \end{pmatrix} \begin{pmatrix} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \end{pmatrix} A=UΣVT⎝⎜⎛616261210−21312131⎠⎟⎞⎝⎛300010⎠⎞(21−212121)
3.6行降维和列降维
通过上面的简单例子,相信大家已经比较了解SVD的求解过程,可能也会有人问过你,SVD这个高大上的东西,有没有更加通俗易懂的理解。本小节站在协方差的角度去理解行降维和列降维,我们先来探讨协方差的含义。协方差里面又分为单变量和多变量的向量之间的计算。
- 单个变量用方差描述,无偏方差公式:
D ( x ) = 1 n − 1 ∑ i = 1 n ( x i − x ‾ ) 2 D(x)=\frac{1}{n-1}\sum^n_{i=1}(x_i-\overline{x})^2 D(x)=n−11i=1∑n(xi−x)2
n是样本数, x ‾ = 1 n ∑ i = 1 n x \overline{x}=\frac{1}{n}\sum^n_{i=1}x x=n1∑i=1nx
- 两个变量用协方差描述,协方差公式:
c o v ( x , y ) = 1 n ∑ i = 1 n ( x i − x ‾ ) ( y i − ( ‾ y ) ) cov(x,y)=\frac{1}{n}\sum^n_{i=1}(x_i-\overline{x})(y_i-\overline(y)) cov(x,y)=n1i=1∑n(xi−x)(yi−(y)) - 多个变量(如三个变量)之间的关系可以用协方差矩阵描述:
c o v ( x , y , z ) = ( c o v ( x , x ) c o v ( x , y ) c o v ( x , z ) c o v ( y , y ) c o v ( y , x ) c o v ( y , z ) c o v ( z , x ) c o v ( z , y ) c o v ( z , z ) ) cov(x,y,z)=\begin{pmatrix} cov(x,x) & cov(x,y) & cov(x,z) \\ cov(y,y) & cov(y,x) & cov(y,z) \\ cov(z,x) & cov(z,y) & cov(z,z) \\ \end{pmatrix} cov(x,y,z)=⎝⎛cov(x,x)cov(y,y)cov(z,x)cov(x,y)cov(y,x)cov(z,y)cov(x,z)cov(y,z)cov(z,z)⎠⎞
相关系数公式:
ρ = c o v ( x , y ) D ( x ) D ( y ) \rho=\frac{cov(x,y)}{\sqrt{D(x)}\sqrt{D(y)}} ρ=D(x)D(y)cov(x,y)
由上式可知, 协 方 差 是 描 述 变 量 间 的 相 关 关 系 程 度 \color{red}协方差是描述变量间的相关关系程度 协方差是描述变量间的相关关系程度:
1)协方差cov(x,y) > 0时,变量x与y正相关;
2)协方差cov(x,y)<0时,变量x与y负相关;
3)协方差cov(x,y)=0时,变量x与y不相关;
变量与协方差关系的定性分析图:
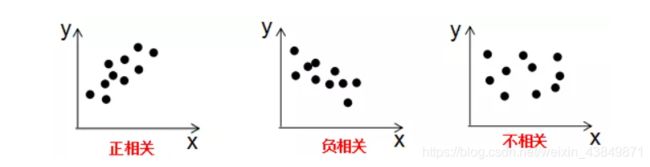
现在开始谈论 A T A 和 A A T A^TA和AA^T ATA和AAT的含义:假设数据集是n维的,共有m个数据,每一行表示一例数据,即:
A = ( ( x ( 1 ) ) T ( x ( 2 ) ) T . . . ( x ( m ) ) T ) A=\begin{pmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ ... \\ (x^{(m)})^T \end{pmatrix} A=⎝⎜⎜⎛(x(1))T(x(2))T...(x(m))T⎠⎟⎟⎞
x ( i ) x^{(i)} x(i)表示第i个样本, x j x_j xj表示第j维特征, x j ( i ) x_j^{(i)} xj(i)表示第i个样本的第j维特征
A T A = ( x ( 1 ) , x ( 2 ) , . . . , x ( m ) ) ( ( x ( 1 ) ) T ( x ( 2 ) ) T . . . ( x ( m ) ) T ) = x ( 1 ) ( x ( 1 ) ) T + x ( 2 ) ( x ( 2 ) ) T + . . . + x ( m ) ( x ( m ) ) T ⇒ A T A = ( c o v ( x 1 , x 1 ) c o v ( x 1 , x 2 ) c o v ( x 1 , x n ) c o v ( x 2 , x 1 ) c o v ( x 2 , x 2 ) c o v ( x 2 , x n ) c o v ( x n , x 1 ) c o v ( x n , x 2 ) c o v ( x n , x n ) ) A^TA=(x^{(1)},x^{(2)},...,x^{(m)})\begin{pmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ ... \\ (x^{(m)})^T \end{pmatrix} =x^{(1)}(x^{(1)})^T+x^{(2)}(x^{(2)})^T+...+x^{(m)}(x^{(m)})^T \\ \Rightarrow A^TA=\begin{pmatrix} cov(x_1,x_1) & cov(x_1,x_2) & cov(x_1,x_n) \\ cov(x_2,x_1) & cov(x_2,x_2) & cov(x_2,x_n) \\ cov(x_n,x_1) & cov(x_n,x_2) & cov(x_n,x_n) \\ \end{pmatrix} ATA=(x(1),x(2),...,x(m))⎝⎜⎜⎛(x(1))T(x(2))T...(x(m))T⎠⎟⎟⎞=x(1)(x(1))T+x(2)(x(2))T+...+x(m)(x(m))T⇒ATA=⎝⎛cov(x1,x1)cov(x2,x1)cov(xn,x1)cov(x1,x2)cov(x2,x2)cov(xn,x2)cov(x1,xn)cov(x2,xn)cov(xn,xn)⎠⎞
由上式可知, A T A A^TA ATA是描述各个特征间关系的矩阵,所以 A T A A^TA ATA的正交基V是以数据集的特征空间进行展开的。
数据集A在特征空间展开为:
X M ∗ N = A M ∗ N V N ∗ N ( 4.1 ) X_{M*N}=A_{M*N}V_{N*N}(4.1) XM∗N=AM∗NVN∗N(4.1)
之前我们说过,特征值表示了 A T A A^TA ATA在相应特征向量的信息分量。特征值越大,包含矩阵 A T A A^TA ATA的信息分量越大。
若我们选择前r个特征值来表示原始数据集,数据集A在特征空间展开为:
X M ∗ r ′ = A M ∗ N V N ∗ r ( 4.2 ) X_{M*r}^{\prime}=A_{M*N}V_{N*r}(4.2) XM∗r′=AM∗NVN∗r(4.2)
( 4.2 ) 式 对 列 进 行 了 降 维 , 即 右 奇 异 矩 阵 V 可 以 用 于 列 数 的 压 缩 , 与 P C A 降 维 算 法 一 致 。 \color{red}(4.2)式对列进行了降维,即右奇异矩阵V可以用于列数的压缩,与PCA降维算法一致。 (4.2)式对列进行了降维,即右奇异矩阵V可以用于列数的压缩,与PCA降维算法一致。
行降维:
A A T = ( ( x ( 1 ) ) T ( x ( 2 ) ) T . . . ( x ( m ) ) T ) ( x ( 1 ) , x ( 2 ) , . . . , x ( m ) ) = ( ( x ( 1 ) ) T x ( 1 ) ( x ( 1 ) ) T x ( 2 ) ( x ( 1 ) ) T x ( m ) ( x ( 2 ) ) T x ( 1 ) ( x ( 2 ) ) T x ( 2 ) ( x ( 2 ) ) T x ( m ) ( x ( m ) ) T x ( 1 ) ( x ( m ) ) T x ( 2 ) ( x ( m ) ) T x ( m ) ) ⇒ A A T = ( c o v ( x 1 , x 1 ) c o v ( x 1 , x 2 ) c o v ( x 1 , x n ) c o v ( x 2 , x 1 ) c o v ( x 2 , x 2 ) c o v ( x 2 , x n ) c o v ( x n , x 1 ) c o v ( x n , x 2 ) c o v ( x n , x n ) ) AA^T=\begin{pmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ ... \\ (x^{(m)})^T \end{pmatrix} (x^{(1)},x^{(2)},...,x^{(m)}) =\begin{pmatrix} (x^{(1)})^Tx^{(1)} & (x^{(1)})^Tx^{(2)} & (x^{(1)})^Tx^{(m)} \\ (x^{(2)})^Tx^{(1)} & (x^{(2)})^Tx^{(2)} & (x^{(2)})^Tx^{(m)} \\ (x^{(m)})^Tx^{(1)} & (x^{(m)})^Tx^{(2)} & (x^{(m)})^Tx^{(m)} \end{pmatrix} \Rightarrow AA^T=\begin{pmatrix} cov(x_1,x_1) & cov(x_1,x_2) & cov(x_1,x_n) \\ cov(x_2,x_1) & cov(x_2,x_2) & cov(x_2,x_n) \\ cov(x_n,x_1) & cov(x_n,x_2) & cov(x_n,x_n) \\ \end{pmatrix} AAT=⎝⎜⎜⎛(x(1))T(x(2))T...(x(m))T⎠⎟⎟⎞(x(1),x(2),...,x(m))=⎝⎛(x(1))Tx(1)(x(2))Tx(1)(x(m))Tx(1)(x(1))Tx(2)(x(2))Tx(2)(x(m))Tx(2)(x(1))Tx(m)(x(2))Tx(m)(x(m))Tx(m)⎠⎞⇒AAT=⎝⎛cov(x1,x1)cov(x2,x1)cov(xn,x1)cov(x1,x2)cov(x2,x2)cov(xn,x2)cov(x1,xn)cov(x2,xn)cov(xn,xn)⎠⎞
由上式可知: A A T AA^T AAT是描述样本数据间相关关系的矩阵,因此,左奇异矩阵U是以样本空间进行展开,原理与列降维一致。
若我们选择前r个特征值来表示原始数据集,数据集A在样本空间展开为:
Y r ∗ N = U r ∗ M A M ∗ N Y_{r*N}=U_{r*M}A_{M*N} Yr∗N=Ur∗MAM∗N
因此,上式实现了行降维,即左奇异矩阵可以用于行数的压缩 。
3.7SVD矩阵分解的应用场景
推荐系统中,我们会面临很多场景,其中有一个问题就是存进数据矩阵是稀疏的,因为用户的很多喜好我们还没有弄明白,留下了很多空白。SVD矩阵分解主要的应用场景就是做数据压缩,比如,图像压缩。为了解决这个问题,我们来看两个数据压缩的方法。
本节介绍两种数据压缩方法:满秩分解和近似分解
矩阵A的秩为k,A的满秩分解:
A M ∗ N = X M ∗ K Y K ∗ N A_{M*N}=X_{M*K}Y_{K*N} AM∗N=XM∗KYK∗N
满秩分解图形如下:
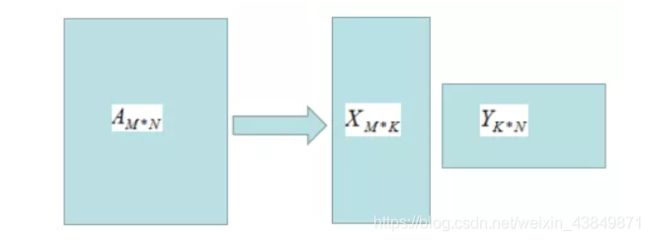
由上图可知,存储X和Y的矩阵比存储A矩阵占用的空间小,因此满秩分解起到了数据压缩作用。
若对数据再次进行压缩,需要用到矩阵的近似分解。
矩阵A的奇异值分解:
A M ∗ N = U M ∗ M V M ∗ N V N ∗ N T A_{M*N}= U_{M*M}V_{M*N}V^T_{N*N} AM∗N=UM∗MVM∗NVN∗NT
A M ∗ N ≃ U M ∗ r V r ∗ N T A_{M*N}\simeq U_{M*r}V_{r*N}^T AM∗N≃UM∗rVr∗NT
如下图:
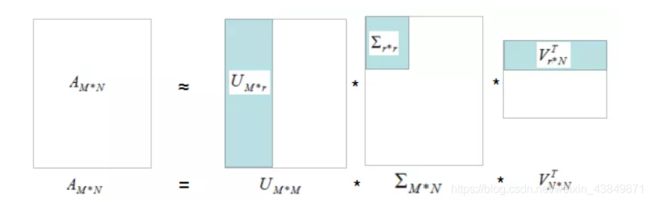
我们用灰色部分的三个小矩阵近似表示矩阵A,存储空间大大的降低了。
3.8 SVD总结
任何矩阵都能进行SVD分解,SVD可以用于行降维和列降维,SVD在数据压缩、推荐系统和语义分析有广泛的应用,SVD与PCA的缺点一样,分解出的矩阵解释性不强 。
4.funkSVD, BiasSVD,SVD++算法
4.1原始SVD
对于任意 m × n m×n m×n矩阵A ,通过奇异值分解,有严格等式
A = P Σ Q T A=P\Sigma Q^T A=PΣQT
其中,P 和Q是方阵, Σ \Sigma Σ是对角矩阵。
进一步的,P的列向量是 m × m m×m m×m方阵 A A T AA^T AAT的特征向量;Q的列向量是 n × n n×n n×n方阵 A T A A^TA ATA的特征向量; m × n m×n m×n矩阵 Σ \Sigma Σ的对角元素是A的特征值。
通过上面的奇异值分解,我们可以将用户-评分矩阵R RR分解为三个矩阵的乘积。
虽然SVD能够将评分矩阵R RR分解,但是存在以下问题
- 原始SVD过程要求评分矩阵R RR是稠密的,但是通常评分矩阵是很稀疏的,这就无法做SVD
- 可以通过填充来让评分矩阵稠密,但是,无论如何填充,都会引入噪音
4.1.1Surprise工具中的SVD
n_factors: k值,默认为100
n_epochs:迭代次数,默认为20
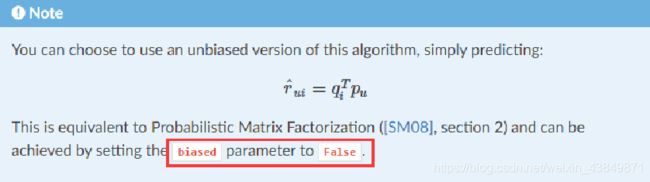
biased:是否使用biasSVD,默认为True
verbose:输出当前epoch,默认为False
reg_all:所有正则化项的统一参数,默认为0.02
reg_bu:bu的正则化参数,reg_bi:bi的正则化参数
reg_pu:pu的正则化参数,reg_qi:qi的正则化参数
4.2FunkSVD
用户-评分矩阵R RR通常是很稀疏的,原始SVD无法使用,因此,我们提出一个近似的矩阵分解算法,FunkSVD。
与MF类似,对于 m × n m×n m×n评分矩阵R,我们假设由两个矩阵 P k × m P_{k×m} Pk×m和 Q k × n Q_{k×n} Qk×n的乘积近似得到,这就意味着下式的成立
R ≈ P T Q R\approx P^TQ R≈PTQ
对于上面的式子,我们可以这样理解
- 评分矩阵 R R R是 m × n m×n m×n的,这就是说,有 m m m个用户和 n n n个商品,每个用户不可能使用所有商品,因此仅仅能对其中少量的商品进行打分,这也就是评分矩阵稀疏的原因
- P P P是 k × m k×m k×m维的,这就是说,我们可以把第 i i i列向量当做用户 i i i的特征 p i p_i pi,这个特征 p i p_i pi是 k k k维的。
- Q Q Q是 k × n k×n k×n维的,这就是说,我们可以把第 j j j列向量当做用户 j j j的特征 q j q_j qj,这个特征 q j q_j qj是 k k k维的。
知道了FunkSVD的原理,我们来讲一个比较通俗的例子:
- 我们有100个用户和1000部电影,用户对看过的电影打分,从而形成用户-商品评分矩阵 R 100 × 100 R_{100×100} R100×100;
- 现在,为了更好的区分不同用户和电影,我们给出3种特征 ( k = 3 ) (k=3) (k=3),分别为 动作,爱情,悬疑;
- 第1个用户的特征 p 1 = [ 0.8 , 0.2 , 0.1 ] T p_1 = [ 0.8 , 0.2 , 0.1 ]^T p1=[0.8,0.2,0.1]T,意思就是这个用户更加偏爱动作,第2部电影的特征 q 2 = [ 0.3 , 0.2 , 0.6 ] T q_2=[0.3, 0.2, 0.6]^T q2=[0.3,0.2,0.6]T,意思是这个电影更加偏向于悬疑;
- 那么,第一个用户看完第二部电影之后的评分,我们预测为 p 1 T ∗ q 2 = = 0.34 p_1^T *q 2 = =0.34 p1T∗q2==0.34,这就是一个综合的喜爱程度
我们想得到这样的 P P P和 Q Q Q,并使得 P T Q P^TQ PTQ尽量接近R。注意, R R R中仅有少量位置存在值,我们求的 P T Q P^TQ PTQ就是尽量接近这些值。
假设 R R R中非空位置集合为 K K K,我们有如下最优化问题
m i n P , Q L = 1 2 ∑ ( i , j ) ∈ K ( R i , j − P i T q j ) 2 + λ 2 ( ∑ i = 1 m ∣ p i ∣ 2 + ∑ j = 1 m ∣ q j ∣ 2 ) min_{P,Q}L=\frac{1}{2}\sum_{(i,j)\in K}(R_{i,j}-P_i^{T}q_j)^2+\frac{\lambda}{2}(\sum_{i=1}^m|p_i|^2+\sum_{j=1}^m|q_j|^2) minP,QL=21(i,j)∈K∑(Ri,j−PiTqj)2+2λ(i=1∑m∣pi∣2+j=1∑m∣qj∣2)
直接对损失函数求导,我们有
∂ L ∂ p i = ∑ j ( p i T q j − R i , j ) q j + λ p i = ( ∑ j q j q j T + λ I ) p i − ∑ j R i , j q j \begin{array}{lcl} \frac{\partial L}{\partial p_i} &=& \sum_j(p_i^{T}q_j-R_{i,j})q_j+\lambda p_i \\ & =& (\sum_j q_jq_j^{T}+\lambda I)p_i-\sum_jR_{i,j}q_j \end{array} ∂pi∂L==∑j(piTqj−Ri,j)qj+λpi(∑jqjqjT+λI)pi−∑jRi,jqj
和 ∂ L ∂ q j = ∑ i ( p i T q j − R i , j ) p i + λ q j = ( ∑ i p i p i T + λ I ) q j − ∑ i R i , j p i \begin{array}{lcl} \frac{\partial L}{\partial q_j} &=& \sum_i(p_i^{T}q_j-R_{i,j})p_i+\lambda q_j \\ & =& (\sum_i p_ip_i^{T}+\lambda I)q_j-\sum_iR_{i,j}p_i \end{array} ∂qj∂L==∑i(piTqj−Ri,j)pi+λqj(∑ipipiT+λI)qj−∑iRi,jpi
因此,更新策略就是:
p i ← p i − α ∂ L ∂ p i q j ← q j − α ∂ L ∂ q j p_i \leftarrow p_i - \alpha \frac{\partial L}{\partial p_i} \\ q_j \leftarrow q_j - \alpha \frac{\partial L}{\partial q_j} \\ pi←pi−α∂pi∂Lqj←qj−α∂qj∂L
α 是 学 习 率 \alpha 是学习率 α是学习率
通过以上迭代更新,可以得到 P P P和 Q Q Q,从而得到近似的评分矩阵 P T Q P^TQ PTQ,从而补全评分矩阵。
4.2.1Surprise工具中的FunkSVD
n_factors: k值,默认为100
n_epochs:迭代次数,默认为20
biased:是否使用biasSVD,设置为True
verbose:输出当前epoch,默认为False
reg_all:所有正则化项的统一参数,默认为0.02
reg_bu:bu的正则化参数,reg_bi:bi的正则化参数
reg_pu:pu的正则化参数,reg_qi:qi的正则化参数
4.3BiasSVD
在FunkSVD的基础上,我们进一步考虑用户偏好和商品偏好。
比如,对于某些用户而言,他们打分一向比较高,而对于较为苛刻的用户,他们打分又偏低;对于某些高质量商品而言,给它们的评分一般偏高,比如泰坦尼克电影评分4.9,可能这部电影没有那么好,被高估了。
基于以上观察,我们有,不同用户有自己的打分习惯,或者偏高或者偏低;不同电影也有自己的分数倾向,或者倾向于低分或者倾向于高分。我们需要在模型中加以体现。
令 μ μ μ为评分的平均值, b i b_i bi为用户 i i i的偏好带来的评分偏置, b j b_j bj为商品 j j j的质量带来的评分偏置。这样,用户 i i i对商品 j j j的评分可以写为
μ + b i + b j + p i T q j μ+b_i+b_j+p_i^{T}q_j μ+bi+bj+piTqj
因此,我们的目标函数可以写为
m i n P , Q , b i , b j L = 1 2 ∑ ( i , j ) ∈ K ( R i , j − μ − b i − b j − p i T q j ) 2 + λ 2 ( ∑ i = 1 m ∣ b i ∣ 2 + ∑ j = 1 n ∣ b j ∣ 2 + ∑ i = 1 m ∣ p i ∣ 2 + ∑ i = 1 m ∣ q j ∣ 2 ) min_{P,Q,b_i,b_j}L=\frac{1}{2}\sum_{(i,j)\in K}(R_{i,j}-μ-b_i-b_j-p_i^{T}q_j)^2+\frac{\lambda}{2}(\sum_{i=1}^m|b_i|^2+\sum_{j=1}^n|b_j|^2+\sum_{i=1}^{m}|p_i|^2+\sum_{i=1}^{m}|q_j|^2) minP,Q,bi,bjL=21(i,j)∈K∑(Ri,j−μ−bi−bj−piTqj)2+2λ(i=1∑m∣bi∣2+j=1∑n∣bj∣2+i=1∑m∣pi∣2+i=1∑m∣qj∣2)
4.3.1Surprise工具中的BiasSVD
n_factors: k值,默认为100
n_epochs:迭代次数,默认为20
biased:是否使用biasSVD,设置为False
verbose:输出当前epoch,默认为False
reg_all:所有正则化项的统一参数,默认为0.02
reg_bu:bu的正则化参数,reg_bi:bi的正则化参数
reg_pu:pu的正则化参数,reg_qi:qi的正则化参数
4.4SVD++
在BiasSVD的基础上,我们进一步考虑用户隐式反馈的影响。
用户除了对商品有评分这一显式反馈之外,还有诸如浏览、点击等隐式反馈。一个用户可能对许多商品有隐式反馈,我们将用户 i i i有过隐式反馈的商品集合记为 N ( i ) N(i) N(i),每一次对于特定商品 s ∈ N ( i ) s\in N(i) s∈N(i)的点击或者浏览,都带来对于用户特征 p i p_i pi的某些偏置 y s y_s ys。
这样,对于用户 i i i,最终他的特征 p i p_i pi可以写为
p i + ∑ s ∈ N ( i ) y s p_i+\sum_{s\in N(i)}y_s pi+s∈N(i)∑ys
因此,用户 i i i对商品 j j j的评分可以写为
μ + b i + b j + q j T ( p i + ∑ s ∈ N ( i ) y s ) μ+b_i+b_j+q_j^{T}(p_i+\sum_{s\in N(i)}y_s) μ+bi+bj+qjT(pi+s∈N(i)∑ys)
这样, 我们的目标函数可以写为
m i n P , Q , b i , b j , y s L = 1 2 ∑ ( i , j ) ∈ K ( R i , j − μ − b i − b j − q j T ( p i + ∑ s ∈ N ( i ) y s ) ) 2 + λ 2 ( ∑ i = 1 m ∣ b i ∣ 2 + ∑ j = 1 n ∣ b j ∣ 2 + ∑ i = 1 m ∣ p i ∣ 2 + ∑ i = 1 m ∣ q j ∣ 2 + ∑ i = 1 m ∑ s ∈ N ( i ) ∣ y s ∣ 2 ) min_{P,Q,b_i,b_j,y_s}L=\frac{1}{2}\sum_{(i,j)\in K}(R_{i,j}-μ-b_i-b_j-q_j^{T}(p_i+\sum_{s\in N(i)}y_s))^2+\frac{\lambda}{2}(\sum_{i=1}^m|b_i|^2+\sum_{j=1}^n|b_j|^2+\sum_{i=1}^{m}|p_i|^2+\sum_{i=1}^{m}|q_j|^2+\sum_{i=1}^{m}\sum_{s\in N(i)}|y_s|^2) minP,Q,bi,bj,ysL=21(i,j)∈K∑(Ri,j−μ−bi−bj−qjT(pi+s∈N(i)∑ys))2+2λ(