排序算法-归并排序

简介

归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

时间复杂度

O(nlogn)

思路分析

排序规则：从小到大

将一个数组拆分成一个个元素，最后将一个个元素两组两组有序合并，最终合并成的数组则是有序的数组。

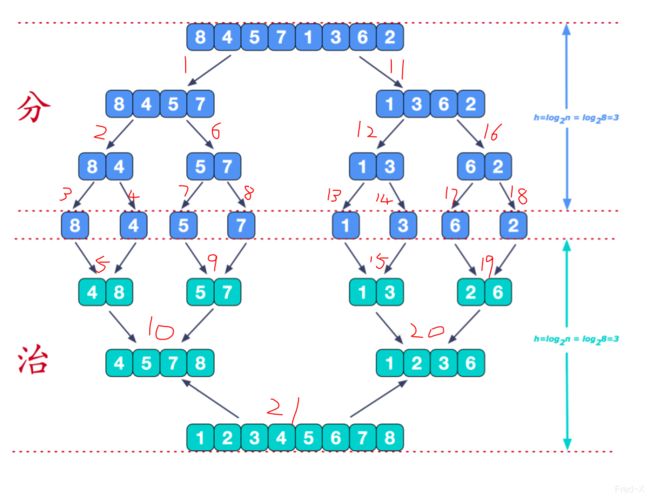
归并排序本质上其实不难，只是在递归拆分时，接触递归比较少的人很难理解他的执行过程，一旦理解了递归的执行流程，归并算法也就理解了。归并算法利用了分治思想，先分后治。下图表示了整个分治过程以及递归执行顺序：

上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，下图是合并的流程（最后一次合并流程，前面n次合并流程也是一样的）

建议简单看一遍图，再读一遍代码，再结合图加代码理解，会有更容易理解。

代码实现

public class MergeSort {
     
    public static void main(String[] args) {
     
        int[] arr = {
     8, 4, 5, 7, 1, 3, 6, 2};
        mergeSort(arr, 0, arr.length - 1, new int[arr.length]);
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 拆分
     *
     * @param arr   待拆分数组
     * @param left  待拆分数组开始索引
     * @param right 待拆分数组结束索引
     * @param temp  合并需要用到的临时数组
     */
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
     
        if (left < right) {
     
            // mid分析
            // left + right >> 1 = mid  左边部分索引   右边部分索引
            //  0   +   8   >> 1 = 4        0-4          5-8
            //  0   +   7   >> 1 = 3        0-3          4-7
            int mid = (left + right) >> 1;
            // 拆分左边部分
            mergeSort(arr, left, mid, temp);
            // 拆分右边部分
            mergeSort(arr, mid + 1, right, temp);
            // 合并
            merge(arr, left, mid, right, temp);
        }
    }

    /**
     * 合并
     *
     * @param arr   待合并的数组
     * @param left  待合并的数组开始索引
     * @param mid   待合并的数组中间索引
     * @param right 待合并的数组结束索引
     * @param temp  合并需要用到的临时数组
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
     
        // left-mid 的当前索引
        int lIndex = left;
        // mid+1-right 的当前索引
        int rIndex = mid + 1;
        // 比较过程中 temp的当前索引
        int tIndex = 0;
        // 1.比较left-mid 和 mid+1-right 一个个元素比较 较小的就放入到temp中
        while (lIndex <= mid && rIndex <= right) {
     
            if (arr[lIndex] < arr[rIndex]) {
     
                temp[tIndex] = arr[lIndex++];
            } else {
     
                temp[tIndex] = arr[rIndex++];
            }
            tIndex++;
            // 上方语句可以简写为下面一句  上方便于理解
            // temp[tIndex++] = arr[lIndex] < arr[rIndex] ? arr[lIndex++] : arr[right++];
        }

        // 2.left-mid 和 mid+1-right 中元素可能比较不均匀  可能left-mid或者mid+1-right中还剩元素
        // 由于left-mid 和 mid+1-right中的元素都分别有序 所以可以直接填充到temp中
        // left-mid中还剩的话就进入循环
        while (lIndex <= mid) {
     
            temp[tIndex++] = arr[lIndex++];
        }
        // mid+1-right中还剩的话就进入循环
        while (rIndex <= right) {
     
            temp[tIndex++] = arr[rIndex++];
        }

        // 3.合并到temp中之后 将temp copy到arr中
        while (tIndex > 0) {
     
            arr[right--] = temp[--tIndex];
        }
    }
}

总结

归并算法是一个稳定的算法，他的合并次数是n-1次，也就是说当有1000个元素时只需要合并999次，排序速度极快。

归并排序重点在于理解递归过程，理解了递归过程就理解了归并排序。归并排序由于使用了递归，所以会占用一定空间，也就是利用空间换时间。