精通数据科学:从线性回归到深度学习(笔记):第四章 线性回归
验旧 制作玩偶数量和成本之间的关系
从机器学习的角度看这个问题
确定场景类型:
(1)我们需要通过生产个数的信息去预测生产成本,而在数据里面,已经有需要被模型预测的量,所以这是一个监督式学习。(2)需要被预测的成本![]() 是一个数量额。它是一个连续变化的量,而并非表示类别的离散量,所以这是一个回归问题。
是一个数量额。它是一个连续变化的量,而并非表示类别的离散量,所以这是一个回归问题。
定义损失函数:
定义一个损失函数(真实值与预测值之间的欧氏距离平方和)。模型参数的估计依赖于这个损失函数。
提取特征:
(1)数据可以直接使用。
(2)变量本身的数学运算是有意义的,可以直接使用(3)可以对X做某种数学变换,得到一个新的特征,比如对它做平方变换。
确定模型形式并估计参数:
(1)根据分析,![]() 和
和![]() 之间是线性关系。
之间是线性关系。
(2)定义模型公式:![]()
(3)参数![]() 的估计值将使损失函数达到最小值。
的估计值将使损失函数达到最小值。
代码:
# -*- coding: UTF-8 -*-
"""
此脚本用于展示使用sklearn搭建线性回归模型
"""
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import linear_model
def evaluateModel(model, testData, features, labels):
"""
计算线性模型的均方差和决定系数
参数
----
model : LinearRegression, 训练完成的线性模型
testData : DataFrame,测试数据
features : list[str],特征名列表
labels : list[str],标签名列表
返回
----
error : np.float64,均方差
score : np.float64,决定系数
"""
# 均方差(The mean squared error),均方差越小越好
error = np.mean(
(model.predict(testData[features]) - testData[labels]) ** 2)
# 决定系数(Coefficient of determination),决定系数越接近1越好
score = model.score(testData[features], testData[labels])
return error, score
def visualizeModel(model, data, features, labels, error, score):
"""
模型可视化
"""
# 为在Matplotlib中显示中文,设置特殊字体
plt.rcParams['font.sans-serif']=['SimHei']
# 创建一个图形框
fig = plt.figure(figsize=(6, 6), dpi=80)
# 在图形框里只画一幅图
ax = fig.add_subplot(111)
# 在Matplotlib中显示中文,需要使用unicode
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.set_title(u'%s' % "线性回归示例")
else:
ax.set_title(u'%s' % "线性回归示例".decode("utf-8"))
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
# 画点图,用蓝色圆点表示原始数据
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.scatter(data[features], data[labels], color='b',
label=u'%s: $y = x + \epsilon$' % "真实值")
else:
ax.scatter(data[features], data[labels], color='b',
label=u'%s: $y = x + \epsilon$' % "真实值".decode("utf-8"))
# 根据截距的正负,打印不同的标签
if model.intercept_ > 0:
# 画线图,用红色线条表示模型结果
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.plot(data[features], model.predict(data[features]), color='r',
label=u'%s: $y = %.3fx$ + %.3f'\
% ("预测值", model.coef_, model.intercept_))
else:
ax.plot(data[features], model.predict(data[features]), color='r',
label=u'%s: $y = %.3fx$ + %.3f'\
% ("预测值".decode("utf-8"), model.coef_, model.intercept_))
else:
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.plot(data[features], model.predict(data[features]), color='r',
label=u'%s: $y = %.3fx$ - %.3f'\
% ("预测值", model.coef_, abs(model.intercept_)))
else:
ax.plot(data[features], model.predict(data[features]), color='r',
label=u'%s: $y = %.3fx$ - %.3f'\
% ("预测值".decode("utf-8"), model.coef_, abs(model.intercept_)))
legend = plt.legend(shadow=True)
legend.get_frame().set_facecolor('#6F93AE')
# 显示均方差和决定系数
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.text(0.99, 0.01,
u'%s%.3f\n%s%.3f'\
% ("均方差:", error, "决定系数:", score),
style='italic', verticalalignment='bottom', horizontalalignment='right',
transform=ax.transAxes, color='m', fontsize=13)
else:
ax.text(0.99, 0.01,
u'%s%.3f\n%s%.3f'\
% ("均方差:".decode("utf-8"), error, "决定系数:".decode("utf-8"), score),
style='italic', verticalalignment='bottom', horizontalalignment='right',
transform=ax.transAxes, color='m', fontsize=13)
# 展示上面所画的图片。图片将阻断程序的运行,直至所有的图片被关闭
# 在Python shell里面,可以设置参数"block=False",使阻断失效。
plt.show()
def trainModel(trainData, features, labels):
"""
利用训练数据,估计模型参数
参数
----
trainData : DataFrame,训练数据集,包含特征和标签
features : 特征名列表
labels : 标签名列表
返回
----
model : LinearRegression, 训练好的线性模型
"""
# 创建一个线性回归模型
model = linear_model.LinearRegression()
# 训练模型,估计模型参数
model.fit(trainData[features], trainData[labels])
return model
def linearModel(data):
"""
线性回归模型建模步骤展示
参数
----
data : DataFrame,建模数据
"""
features = ["x"]
labels = ["y"]
# 划分训练集和测试集
trainData = data[:15]
testData = data[15:]
# 产生并训练模型
model = trainModel(trainData, features, labels)
# 评价模型效果
error, score = evaluateModel(model, testData, features, labels)
# 图形化模型结果
visualizeModel(model, data, features, labels, error, score)
def readData(path):
"""
使用pandas读取数据
"""
data = pd.read_csv(path)
return data
if __name__ == "__main__":
homePath = os.path.dirname(os.path.abspath(__file__))
# Windows下的存储路径与Linux并不相同
if os.name == "nt":
dataPath = "%s\\data\\simple_example.csv" % homePath
else:
dataPath = "%s/data/simple_example.csv" % homePath
data = readData(dataPath)
linearModel(data)从统计学的角度看这个问题
- (1)假设条件概率:
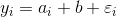
代码:
# -*- coding: UTF-8 -*-
"""
此脚本用于展示如何使用statsmodels搭建线性回归模型
"""
# 保证脚本与Python3兼容
from __future__ import print_function
import os
import sys
import numpy as np
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
import matplotlib.pyplot as plt
import pandas as pd
def modelSummary(re):
"""
分析线性回归模型的统计性质
"""
# 整体统计分析结果
print(re.summary())
# 在Windows下运行此脚本需确保Windows下的命令提示符(cmd)能显示中文
# 用f test检测x对应的系数a是否显著
print("检验假设x的系数等于0:")
print(re.f_test("x=0"))
# 用f test检测常量b是否显著
print("检测假设const的系数等于0:")
print(re.f_test("const=0"))
# 用f test检测a=1, b=0同时成立的显著性
print("检测假设x的系数等于1和const的系数等于0同时成立:")
print(re.f_test(["x=1", "const=0"]))
def visualizeModel(re, data, features, labels):
"""
模型可视化
"""
# 计算预测结果的标准差,预测下界,预测上界
prstd, preLow, preUp = wls_prediction_std(re, alpha=0.05)
# 为在Matplotlib中显示中文,设置特殊字体
plt.rcParams['font.sans-serif']=['SimHei']
# 创建一个图形框
fig = plt.figure(figsize=(6, 6), dpi=80)
# 在图形框里只画一幅图
ax = fig.add_subplot(111)
# 在Matplotlib中显示中文,需要使用unicode
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.set_title(u'%s' % "线性回归统计分析示例")
else:
ax.set_title(u'%s' % "线性回归统计分析示例".decode("utf-8"))
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
# 画点图,用蓝色圆点表示原始数据
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.scatter(data[features], data[labels], color='b',
label=u'%s: $y = x + \epsilon$' % "真实值")
else:
ax.scatter(data[features], data[labels], color='b',
label=u'%s: $y = x + \epsilon$' % "真实值".decode("utf-8"))
# 画线图,用红色虚线表示95%置信区间
# 在Python3中,str不需要decode
if sys.version_info[0] == 3:
ax.plot(data[features], preUp, "r--", label=u'%s' % "95%置信区间")
ax.plot(data[features], re.predict(data[features]), color='r',
label=u'%s: $y = %.3fx$'\
% ("预测值", re.params[features]))
else:
ax.plot(data[features], preUp, "r--", label=u'%s' % "95%置信区间".decode("utf-8"))
ax.plot(data[features], re.predict(data[features]), color='r',
label=u'%s: $y = %.3fx$'\
% ("预测值".decode("utf-8"), re.params[features]))
ax.plot(data[features], preLow, "r--")
legend = plt.legend(shadow=True)
legend.get_frame().set_facecolor('#6F93AE')
plt.show()
def trainModel(X, Y):
"""
训练模型
"""
model = sm.OLS(Y, X)
re = model.fit()
return re
def linearModel(data):
"""
线性回归统计性质分析步骤展示
参数
----
data : DataFrame,建模数据
"""
features = ["x"]
labels = ["y"]
Y = data[labels]
# 加入常量变量
X = sm.add_constant(data[features])
# 构建模型
re = trainModel(X, Y)
# 分析模型效果
modelSummary(re)
# const并不显著,去掉这个常量变量
resNew = trainModel(data[features], Y)
# 输出新模型的分析结果
print(resNew.summary())
# 将模型结果可视化
visualizeModel(resNew, data, features, labels)
def readData(path):
"""
使用pandas读取数据
"""
data = pd.read_csv(path)
return data
if __name__ == "__main__":
homePath = os.path.dirname(os.path.abspath(__file__))
# Windows下的存储路径与Linux并不相同
if os.name == "nt":
dataPath = "%s\\data\\simple_example.csv" % homePath
else:
dataPath = "%s/data/simple_example.csv" % homePath
data = readData(dataPath)
linearModel(data)
模型陷阱
- (1)模型的预测效果不稳定,实际准确度与预估值相比,相差甚远。
- (2)模型没能抓住数据真正的内在关系,错误地估计预测值与自变量之间的联动效应,即对应的参数。
原因:
-
过度拟合:
- 当模型太过简单时,无论是训练误差还是测试误差都很高,也就是说太过简单的模型还不足以捕捉数据里的复杂关系。
- 当模型太过复杂时,,训练误差很小,但测试误差却相当高,这就是过度拟合。与模型太过简单相比,过度拟合是更加危险的,因为它具有极强的迷惑性,容易让人误以为模型的结果很理想。
- 模型幻觉:将毫不相关的变量放到模型,造成模型幻觉。
模型幻觉之统计学方案:假设检验
模型幻觉之机器学习方案:惩罚项
在原有的损失函数里加入惩罚项(或者叫正则化想),将损失函数改写成如下形式:
![]()
使得那些本该等于0的参数估计值尽量往0靠近。
比较两种方案
假设检验在数学上更加严谨,有一系列的理论做支撑。我们可以根据检验结果完全排除掉不相关变量的干扰。但是通过上面的示例可以看到,它的整个过程需要较多的人为干预,并不能做到完全自动化。而且在数据量小时,容易发生误判情况,即把相关变量判定为不相关的,进而将其舍弃,得到错误的模型。
惩罚项这个解决方案恰好相反,它可以做到完全自动化,整个过程不需要人为干预。但是缺点在于理论基础不牢靠,对于结果的解释性较差。很难通过比较简单的语言将方案解释给非技术人员。