金融经济学（王江）期末梳理 第十三章 资本资产定价模型（CAPM）

Introduction

上一章，我们证明了，参与者会选择无风险资产和切点组合进行组合选择，即选择存在无风险证券市的有效前沿组合MVE，所以所有参与者之间最大的不同就是对切点组合和无风险组合之间权重的分配，所以所有参与者加总为代表性参与者。当市场中总需求和总供给达到均衡时，我们就能够求得市场的均衡定价，也就是构造了一个资产定价模型。

13.1 证券市场均衡

13.1.1 市场组合

和前面类似，我们把市场上所有公司发行的股票和债券加总，就得到了市场上证券的总供给，也就是市场组合，同时也是未来消费的总禀赋，市场组合${\theta }_M$可以用市场上每种证券的总股数来表示，也可以用权重来表示。下面定义几个概念：

（1）令${\overline{\theta }}_n$为第n中债券的总股数，那么市场组合可以表示为
${\theta }_M=[{\overline{\theta }}_1;{\overline{\theta }}_2;\dots ;{\overline{\theta }}_N]$

（2） $P=[P_1;P_2\dots ;P_N]$为所有证券的价格向量

（3）证券n的总市值：$v_n=P_n{\overline{\theta }}_n$ 市场组合的总市值：$v_M=P^T{\theta }_M$

（4）证券n的相对市值权重$z_M$,${}_n=v_n/v_M=$$\frac{P_n{\overline{\theta }}_n}{P^T{\theta }_M}$
用组合权重来表示市场组合$z_M=[z_1;z_2;\dots ;z_N]$

13.1.2 证券市场总需求

存在无风险证券时，每个参与者对风险资产的需求都是切点组合，只是每个参与者的需求量不同。

13.1.3 市场均衡：市场出清

在均值-方差偏好下，市场达到均衡时，市场组合就是切点组合。

证明：假设$a_k$为第k个参与者投资与切点组合的投资额，那么$w_k-a_k$就是参与者k投资于无风险资产上的投资额。

首先我们对无风险资产进行分析：无风险资产出清意味着借=贷

所以${\sum }_k(w_k-a_k)=0$ （1）

风险证券出清：${\sum }_k{a}_k{z}_T=({\sum }_k{a}_k)z_T=v_M{z}_M$（2）（总市值乘以相对市值权重就是每个证券的供给量即市场组合）

（对于参与者是所有投资额$\sum w_k$ 对于公司是所有融资额$v_M$）

将（1）带入 （2）有 $v_M{z}_M={\sum }_k{w}_k{z}_M={\sum }_k{w}_k{z}_T$

所以$z_M=z_T$,即市场组合就是切点组合。

那么，进一步认为，所有参与者的组合选择都是无风险资产和市场组合的组合。

13.2 资本资产定价模型

13.2.1 存在无风险资产的CAPM

1、推导

在上一章，我们得到了切点组合的CAPM，现在用市场组合代替切点组合，有${\overline{r}}_n-r_F={\beta }_n({\overline{r}}_M-r_F)$ , 其中${\beta }_n=$ $\frac{Cov({\tilde{r}}_n,{\tilde{r}}_M)}{{\sigma }_M^2}$.

2、意义

一个资产的风险溢价与其市场风险成正比，其市场风险由它对市场组合风险的贡献即β来决定，比例系数是市场组合的风险溢价，由于市场组合的β为1，所以市场组合的风险溢价也叫做风险价格，这里β是解释变量。

3、SML

由上述关系，我们将β值作为横坐标，资产的风险溢价作为纵坐标，即可得到向上的证券市场线，描述了一个证券的风险溢价和其市场风险的关系，如图所示

值得注意的是，在第十章我们基于消费的CAPM得到了类似的关系式，但其只是一个近似，虽然可以严格证明但是其用来替代未来消费的组合q，在现实中是观察不到的。而我们在均值方差偏好的假设下，得到了CAPM，是严格的均衡定价公式。

4、应用

（1）我们作资产收益率对市场收益率的线性回归有：

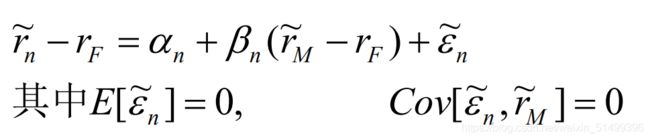
（2）CAPM要求阶矩项α=0，这样将资产收益率的风险分解为两个部分:

只有市场风险才有溢价，剩余风险没有溢价。
溢价大小取决于其负载的系统风险，取决于其β值。风险价格是市场组合的溢价。
（3）均值-方差框架下，收益率方差度量了资产的总风险
即 ${\sigma }_n^2={\beta }_n^2{\sigma }_M^2+{\sigma }_{\epsilon }^2$, 如果用方差来代表风险的话，资产的风险就可以分解为资产负载的市场风险和剩余风险之和。其市场风险/资产风险就是回归的拟合优度$R^2$,所以用该证券负载的市场风险能很好的拟合资产的风险。
（4）β为正，市场指数； β为负，套期保值

13.2.2 不存在无风险资产的CAPM

（1）首先，根据第十二章 任意组合q与均值方差前沿组合的收益率关系:

所以只要证明市场均衡时市场组合可以替代均值方差前沿组合p即可推导出不存在无风险证券时的CAPM。

（2）不存在无风险证券时

step1:参与者k对证券的组合选择：

$z_k=z_0+(z_1-z_0){\overline{r}}_k$

step2:对于参与者k的对证券的需求量：

$w_k{z}_k=w_k(z_0+(z_1-z_0){\overline{r}}_k)$

step3:市场出清条件为：

${\sum }_k{w}_k(z_0+(z_1-z_0){\overline{r}}_k)=v_M{z}_M$

整理得：
$z_0+(z_1-z_0)$$\frac{{\sum }_k{w}_k{\overline{r}}_k}{v_M}$ $=z_M$

可以看到市场组合可以由均值方差前沿上$z_0,z_1$这两个组合构造，而任意均值方差前沿组合也可由均值方差前沿上$z_0,z_1$这两个组合构造。所以市场组合可以是均值方差前沿组合之一。由（1）可知：

这就是不存在无风险证券是得资本资产定价模型，存在无风险证券只是它得一个特例，即与市场组合不相关的证券取无风险证券即可。

13.3 一般均衡框架下的CAPM

从12章到13章，我们在均值-方差框架下利用优化理论，推导出了CAPM。还记得，在介绍均值-方差框架之前，我们给出了两种情况下参与者有均值方差偏好，那么在不舍弃效用函数的情况下，如何直接从参与者一般均衡框架中推导CAPM呢？下面介绍两种情况:

13.3.1 二次效用函数的均值-方差偏好

1、假设条件

1期具有二次效用函数，给定：$u_k(c)=u_0(c_0)+(a_k/2)(c_1-{\overline{c}}_k{)}^2$

2、由组合选择的欧拉方程

对于每个证券q

$E[u_1^{\prime }({\tilde{c}}_1)({\tilde{r}}_q-r_F)]=a_{k}E[({\tilde{c}}_1-{\overline{c}}_k)({\tilde{r}}_q-r_F)]=0$

3、对参与者求和

$E[({\tilde{C}}_1-\overline{C})({\tilde{r}}_q-r_F)]=0$

${\tilde{C}}_1$是1其总消费

$\overline{C}$是每个参与者0期消费的加总（0期消费越多，1期效用越差）（？）这个是什么是不影响推导的

整理有：

$E[{\tilde{C}}_1-{\overline{C}}_1+{\overline{C}}_1-\overline{C})({\tilde{r}}_q-{\overline{r}}_q+{\overline{r}}_q-r_F)]=$

$E[({\tilde{C}}_1-{\overline{C}}_1)({\tilde{r}}_q-{\overline{r}}_q)+({\tilde{C}}_1-\overline{C})({\overline{r}}_q-r_F)]=0$

4、求出${\overline{r}}_q-r_F$

$Cov({\tilde{C}}_1,{\tilde{r}}_q)+E[({\tilde{C}}_1-\overline{C})({\overline{r}}_q-r_F)$=0

所以${\overline{r}}_q-r_F=$-$\frac{Cov({\tilde{C}}_1,{\tilde{r}}_q)}{E[({\tilde{C}}_1-\overline{C})}$

5、由市场出清：${\tilde{C}}_1=v_M(1+{\tilde{r}}_M)$

${\overline{r}}_q-r_F=$-$\frac{v_{M}Cov({\tilde{r}}_M,{\tilde{r}}_q)}{E[({\tilde{C}}_1-\overline{C})}$ (1)

6、取q为市场组合：

${\overline{r}}_M-r_F=$-$\frac{v_M{\sigma }_M^2}{E[({\tilde{C}}_1-\overline{C})}$ (2)

(1)/(2)有
${\overline{r}}_q-r_F=({\overline{r}}_M-r_F)$$\frac{Cov({\tilde{r}}_M,{\tilde{r}}_q)}{{\sigma }_M^2}$
这就是二次效用函数的CAPM。

13.3.2 正态分布的支付**

1、假设条件

（1）风险证券在1期得到支付为${\tilde{v}}_n$ 即市值的未来支付
$\tilde{v}$为所有证券的支付向量
假设$\tilde{v}$是服从N维正态分布的，均值和方差分别为$\overline{v},\sum$
S为风险证券的价格向量
（2）K个参与者，k初始禀赋为$e_k$,${}_0和{\overline{\theta }}_k$.无风险证券总供给为0.投资额为$w_k=e_k$,${}_0+S^T{\theta }_k-c_k$,${}_0$.
（3）1期效用函数具有不变的绝对风险厌恶系数$a_k$即效用函数为
$u_k(c)=u_0(c_0)-exp(-a_k{c}_k$,${}_1)$

$c_k$,${}_1=w_k(1+r_F)+{\theta }_k^T[\tilde{v}-(1+r_F)S]$ 服从正态分布

$E[{\tilde{w}}_k]=w_k(1+r_F)+{\theta }_k^T[\overline{v}-(1+r_F)S]$

$Var[{\tilde{w}}_k]={\theta }_k^T\sum {\theta }_k$

2、正态分布性质：

$E[-exp(-a_k{\tilde{w}}_k)]=-exp[-a_{k}E[{\tilde{w}}_k]+1/2(a_k^{2}Var({\tilde{w}}_k))]$

3、优化问题简化

max $E[-exp(-a_k{\tilde{w}}_k)]$ 等价于 ：

max $E[{\tilde{w}}_k]-1/2(a_{k}Var({\tilde{w}}_k))]$

max $w_k(1+r_F)+{\theta }_k^T[\overline{v}-(1+r_F)S]-1/2a_k{\theta }_k^T\sum {\theta }_k$

4、求解：

一阶条件：

$\overline{v}-(1+r_F)S-a_k\sum {\theta }_k=0$

$\sum {\theta }_k=$ $\frac{\overline{v}-(1+r_F)S}{a_k}$

${\theta }_k={\sum }^{-}$ ${}^1$$\frac{\overline{v}-(1+r_F)S}{a_k}$

市场出清：

（1）${\sum }_k{\theta }_k=\overline{\theta }$

$\overline{\theta }={\sum }_k{\sum }^{-}$ ${}^1$ $\frac{\overline{v}-(1+r_F)S}{a_k}$

$={\sum }_k$ $\frac{1}{a_k}$${\sum }^{-}$ ${}^1$$\overline{v}-(1+r_F)S$

（2）令$1/\alpha ={\sum }_k$ $\frac{1}{a_k}$

则 $\overline{\theta }={\sum }_k$ $\frac{1}{a_k}$${\sum }^{-}$ ${}^1$ ($\overline v-(1+r_F)S)=$1/\alpha {\sum }^{-}$ ${}^1$ $(\overline{v}-(1+r_F)S)$

则 $\overline{v}-(1+r_F)S=\sum \overline{\theta }\alpha$ （均衡定价公式）

均衡定价方程左乘 ${\overline{\theta }}^T$求解市场组合收益率（类似令p=市场组合）

${\overline{\theta }}^T\overline{v}-{\overline{\theta }}^T(1+r_F)S={\overline{\theta }}^T\sum \overline{\theta }\alpha$

${\tilde{w}}_M-w_M(1+r_F)={\overline{\theta }}^T\sum \overline{\theta }\alpha$

同时除以$w_M$

${\overline{x}}_M-(1+r_F)=$$\frac{{\overline{\theta }}^T\sum \overline{\theta }\alpha }{w_M}$

${\overline{r}}_M-r_F=$$\frac{{\overline{\theta }}^T\sum \overline{\theta }\alpha }{w_M}$（1）

均衡定价方程求解证券期望收益率：

$\overline{v}-(1+r_F)S=\sum \overline{\theta }\alpha$

共N个方程，每个方程对应一个证券

对于某一个证券，同时除以Sn

${\overline{x}}_n-(1+r_F)=(\alpha /S_n)(\sum \overline{\theta }{)}_n$

${\overline{r}}_n-r_F=(\alpha /S_n)(\sum \overline{\theta }{)}_n$ (2)

由上一节：${\overline{r}}_M-r_F=$$\frac{{\overline{\theta }}^T\sum \overline{\theta }\alpha }{w_M}$ (1)

(1)/(2)有

${\overline{r}}_n-r_F=({\overline{r}}_M-r_F)$ $\frac{w_m}{S_n}$ $\frac{（\sum \overline{\theta }{)}_n}{{\overline{\theta }}^T\sum \overline{\theta }}$

验证β

这样就求出了类似CAPM的形式，下面我们验证系数是否是β

首先市场组合收益率为${\tilde{r}}_M=$ $\frac{{\overline{\theta }}^T\tilde{v}}{w_M}$

那么市场组合和证券n的协方差

$Cov({\tilde{r}}_M,{\tilde{r}}_n)=$$\frac{CoV({\theta }^T\tilde{v},{\tilde{v}}_n)}{v_M{S}_n}$ =$\frac{(\sum \overline{\theta }{)}_n}{v_M{S}_n}$

$Var({\tilde{r}}_M)=$ $\frac{{\overline{\theta }}^T\sum \overline{\theta }}{v_M^2}$

我们得到了${\beta }_n=$$\frac{(\sum \overline{\theta }{)}_n}{v_M{S}_n}/\frac{{\overline{\theta }}^T\sum \overline{\theta }}{v_M^2}$= $\frac{v_m}{S_n}$ $\frac{(\sum \overline{\theta }{)}_n}{{\overline{\theta }}^T\sum \overline{\theta }}$

与上面求到的CAPM模型不谋而合：
${\overline{r}}_n-r_F=({\overline{r}}_M-r_F)$ $\frac{w_m}{S_n}$ $\frac{（\sum \overline{\theta }{)}_n}{{\overline{\theta }}^T\sum \overline{\theta }}$
得证。