金融经济学(王江)期末梳理 第十五章 完全市场下的公司财务

Introduction

前面所有分析都是建立在第二章所描述的基本框架中，这一章将此框架拓展到存在生产机会的情形。大致思路是首先确定最优生产决策，然后将生产决策加入约束中求解消费者期望效用最大以及市场均衡。

什么是生产? 将现有资源(禀赋)转化为未来禀赋的过程。这种转化能力叫做生产能力，可由下面生产函数表示：$y_k$ ,${}_1=y_k(y_0)$.
我们假设生产函数具有边际报酬递减规律。为了简便设起点为0。

15.1 最优生产策略

15.1.1 预算约束

生产技术

$\varphi$为状态价格向量 $y_k$是一个函数表示生产技术，0期投入是$y_k$${}_0$

生产净市值

这些产出的现市值就是${\varphi }^T{y}_k$${}_1$

生产技术的净市值（即生产技术带来的收益）记作$v_k={\varphi }^T{y}_k$ ${}_1-y_k$${}_0$.

（1）依赖于投入和生产函数，我们分析时，假定生产技术不变。但是投入是由投资者来决定的即投资决策。
（2）可正可负，因为边际报酬递减，当超出一定规模时，产出将低于投入。

财富

$w_k=e_k,$ ${}_0-y_k$,${}_0+{\varphi }^T(e_k,$${}_1+y_k$,${}_1)$

意味着0期禀赋的减少和1期禀赋的增加

所以参与者进行消费和投资选择的预算约束为：

$c_k$,${}_0+{\varphi }^T{c}_k,$ ${}_1=w_k=e_k,$ ${}_0-y_k$,${}_0+{\varphi }^T(e_k,$${}_1+y_k$,${}_1)$

在原来约束约束的基础上加入生产决策。

15.1.2 消费和投资决策

第一步：求解初始投入生产的数量 $y_k$,${}_0$

财富最大化：max $w_k=e_k,$ ${}_0-y_k$,${}_0+{\varphi }^T(e_k,$${}_1+y_k$,${}_1)$

一阶条件对 $y_k$,${}_0$求导${\varphi }^T{y}_k^{\prime }=1$，显然最优生产决策处于规模效率的点即规模报酬不变。

由于$y_k$严格凹，所以二阶条件自动满足，从而解出$y_k$,${}_0$
如过$y_k$,${}_0>e_0$呢？可以通过证券市场筹集这部分资金。

第二步：优化问题求解：均衡配置

等价于前面基于消费的优化问题求解，这一步投入和产出是常数。所以解的形式和前面相同：

第三步：市场出清：均衡价格

我们知道，在1期消费1期禀赋和投入得到的生产：

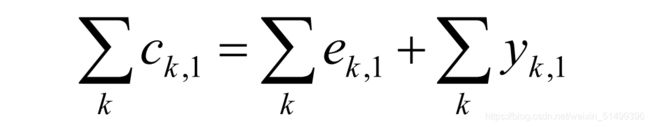
将1期市场出清条件折现到0期，与预算约束比较可以得到0期商品市场出清。

15.1.3 代表性参与者

其中每个参与者的配置等同于在市场达到均衡时的配置，可以通过状态价格来寻找二者之间的关系。

15.2 公司财务

15.2.1 投资决策

引入公司

上一节我们认为每个参与者都有生产技术，然而现实中公司拥有生产技术，假设每个公司的股票都由参与者持有.

公司净市值最大化

参与者k持有公司f的股份比例为$s_k$,${}_f$对于某个企业f ${\sum }_k{s}_k$,${}_f=1$，

所以某个企业在0期的市场净值为：$v_f={\varphi }^T{y}_f(y_0)-y_0$

企业投资决策目标使市场净值最大化，一阶条件为：${\varphi }^T{y}_f^{\prime }=1$

可以看到这个条件只依赖于证券价格和生产函数，与公司的禀赋和偏好无关，即无论公司归谁所有，大家都会做出一样的决策。所以，由谁来管理公司都一样，这位管理权和经营权的分离提供了理论基础。

参与者总财富

参与者k持有的总股份为 ${\sum }_f{s}_k$,${}_f$

所以参与者k持有的总财富为：$w_k=e_0+{\varphi }^T{e}_1+{\sum }_f{s}_k$,${}_f{v}_f$

与上面相比，参与者净值变为参与者持有公司净值的一个累加项。

股东决策定理

在一个完全和竞争的证券市场中，企业股东对企业的投资决策具有一致的目标，那就是最大化企业的市场价值。

如何理解：我们知道，如果市场是完全的，参与者想要得到更多的消费计划，必须要有更多的财富，所以公司的所有者股东对企业的要求就是为他们创造更多的财富即净市值最大化。

15.2.2 融资决策

融资决策：企业如何筹集资金$y_0$
融资方式：股权和债权
债券融资：$d_0$
股权融资：$y_0-d_0$
资本结构：融资所用的证券组合

资本结构分析

公司未来总支付可以分解为两部分，股权支付和债权支付即
$y_1=e_1+d_1$
公司资产的价值即公司未来总支付的现值：V=D+E=${\varphi }^T{y}_1$
股权支付的现值：$E={\varphi }^T{e}_1$
债券支付的现值：$D={\varphi }^T{d}_1=d_0$
股东的权益净值：$v=E-e_0={\varphi }^T(y_1-d_1)-e_0=$

${\varphi }^T{y}_1-{\varphi }^T{d}_1-e_0={\varphi }^T{y}_1-y_0$

如果股东的决策仍然使股东权益净值最大化，那么其决策与债权和股权选择无关，只取决于融资数量和生产函数，这就是著名的MM定理

MM定理

在完全证券市场下，企业价值只由它的投资决策决定而与其融资决策无关。

解释：企业净现值取决于它的投资决策，而融资决策的选择，只会改变其未来现金流在某种融资方式上的分配，即如何划分饼的大小，而无法将饼划分的更大。

15.3 NPV法则

参与者只会选择所有净现值为正的项目投资。
我们利用资产定价的欧拉方程来表示未来支付的现值，δ为投入。

所以:NPV = $\frac{E[{\tilde{y}}_j]}{1+{\mu }_j}$$-y_0$