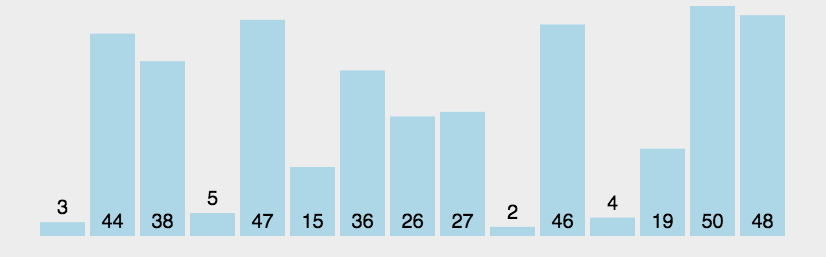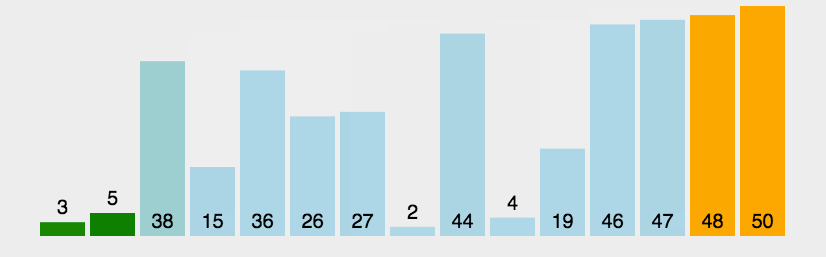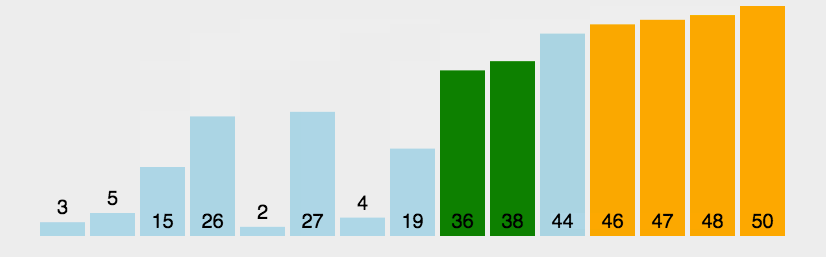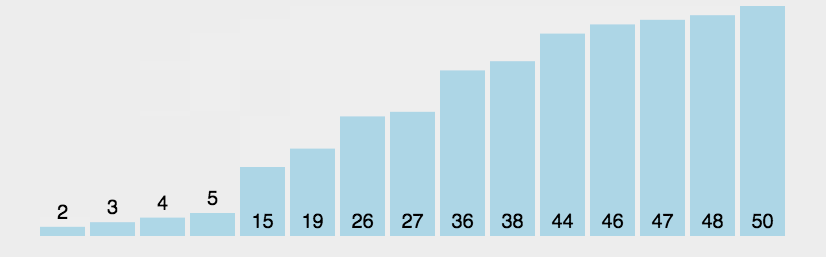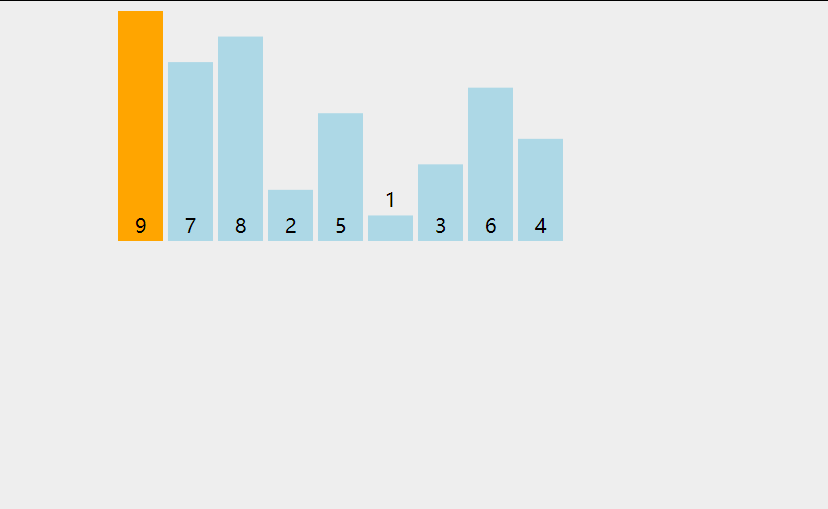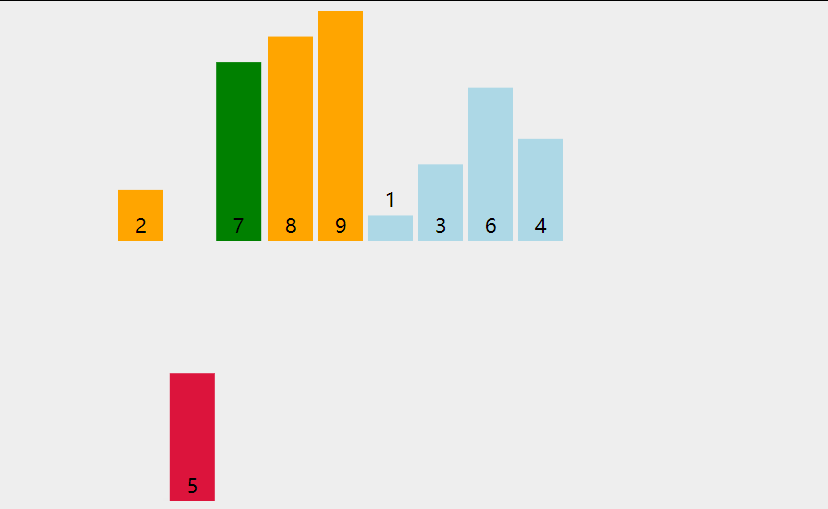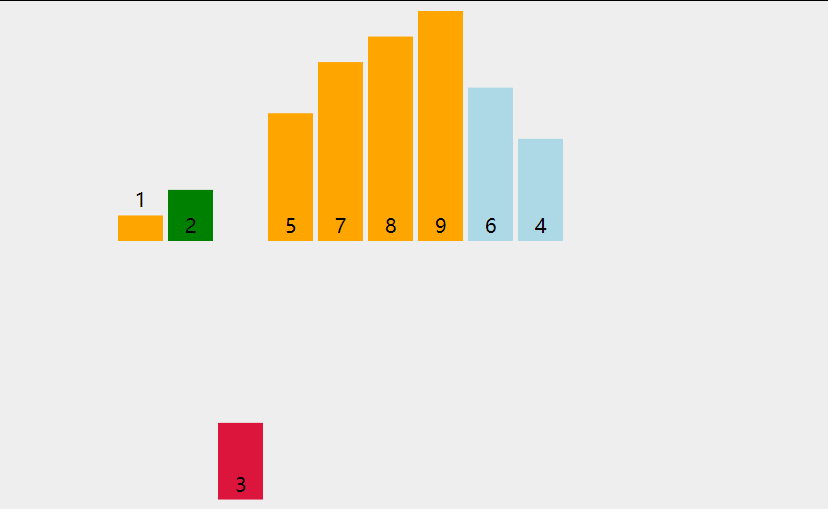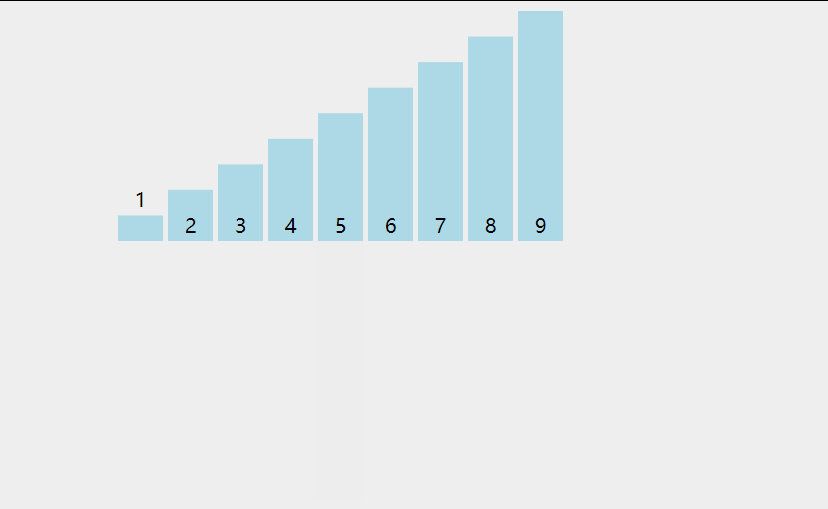位运算符与算法排序
位运算符
位运算符比一般的算术运算符速度要快,而且可以实现一些算术运算符不能实现的功能。如果要开发高效率程序,位运算符是必不可少的。位运算符用来对二进制位进行操作,包括:按位与(&)、按位或(|)、按位异或(^)、按位取反(~)、按位左移(<<)、按位右移(>>)。
按位与(&)
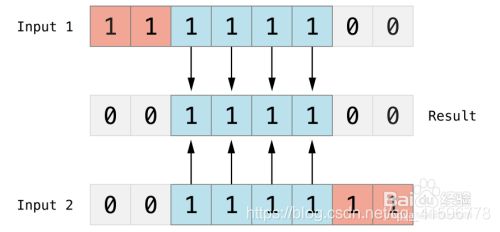
对两个数进行操作,然后返回一个新的数,这个数的每个位都需要两个输入数的同一位都为1时才为1,如下图:
(A & B) 结果为 12, 二进制为 0000 1100
按位或(|)
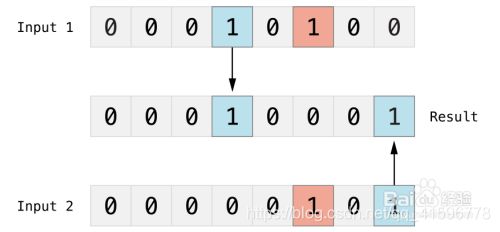
比较两个数,然后返回一个新的数,这个数的每一位设置1的条件是两个输入数的同一位都不为0(即任意一个为1,或都为1),如下图:
(A | B) 结果为 61, 二进制为 0011 1101
按位异或(^)
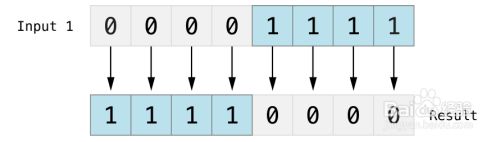
比较两个数,然后返回一个数,这个数的每个位设为1的条件是两个输入数的同一位不同,如果相同就设为0,如下图:
(A ^ B) 结果为 49, 二进制为 0011 0001
按位取反(~)
对一个操作数的每一位都取反,如下图:
(~A ) 结果为 -61, 二进制为 1100 0011
按位左移(<<)
将操作数的所有位向左移动指定的位数。
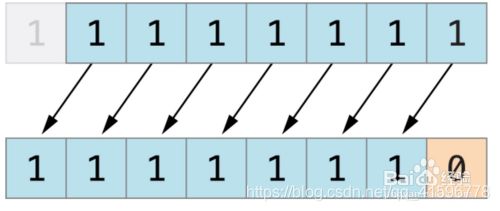
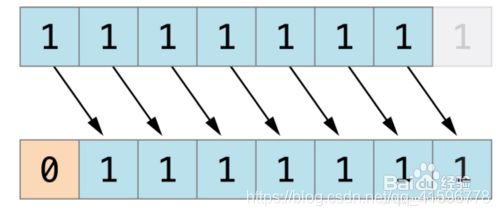
下图展示了11111111 << 1(11111111 左移一位)的结果。蓝色数字表示被移动位,灰色表示被丢弃位,空位用橙色的0填充。相当于乘以二。
(A << 2)结果为 240, 二进制为 1111 0000
按位右移(<<)
将操作数的所有位向又移动指定的位数。
下图展示了11111111 >> 1(11111111 右移一位)的结果。蓝色数字表示被移动位,灰色表示被丢弃位,空位用橙色的0填充。相当于除以2。
A >> 2 结果为 15, 二进制为 0000 1111
运算符的优先级
() 括号优先级最高
** 优先级其次
= 优先级最低
一元运算符:同一时间只操作一个数字的 (- , ~)
二元运算符:同一时间能操作二个数字的 (+ , -...)
~19+5
一般来说,一元运算符 大于 二元运算符的优先级
+ - * / => * / 大于 + -
() not and or => not > and > or
如果都是二元运算符:
算术运算符 > 位运算符 > 比较运算符 > 身份运算符 > 成员运算符 > 逻辑运算符
赋值运算符 作为最后等号右边的值算好后进行赋值.
小练习
1、请实现两个整数变量的交换(不能使用第三方变量)
2、最有效率的算出2 * 8的结果
答案分析
1、实现两个整数变量的交换很简单,但是这道题目却明确指出不能使用第三方变量。有两种方法。
方法一:
int a = 20;int b = 10;
a = a + b;
b = a - b;
a = a - b;
方法一有个缺点,如果数值超出了int类型的取值范围,将会损失精度
方法二:
int a = 20;
int b = 10;
a = a ^ b;
b = a ^ b;
a = a ^ b;
2、直接操作二进制是比较快的,所以使用左移符号
System.out.println(2 << 3);
算法
排序算法
排序的结果有两种:
- 升序
- 降序
冒泡排序
算法步骤
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。 [1]
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在 这一点,最后的元素应该会是最大的数。 [1]
- 针对所有的元素重复以上的步骤,除了最后一个。 [1]
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需 要比较。 [1]
图片演示
有8个数组组成一个无序数列:5,8,6,3,9,2,1,7,希望从大到小排序。按照冒泡排序的思想,我们要把相邻的元素两两进行比较,根据大小交换元素的位置,过程如下:
第一轮排序:
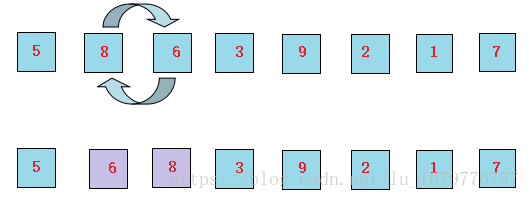
1、首先让5和8进行交换,发现5比8小,因此元素位置不变。
2、接下来让8和6比较,发现8比6大,所以要交换8和6的位置。
3、继续让8和3比较,发现8比3要大,所以8和3 交换位置。
4、继续让8和9进行比较,发现8比9小,不用交换
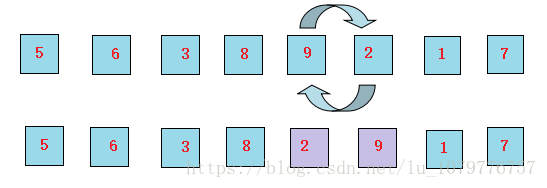
5、9和2进行比较,发现9比2大,进行交换
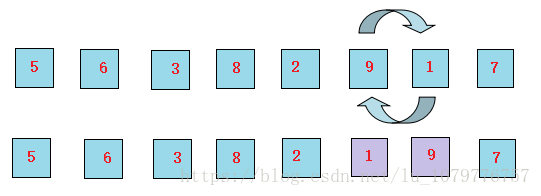
6、继续让9和1进行比较,发现9比1大,所以交换9和1的位置。
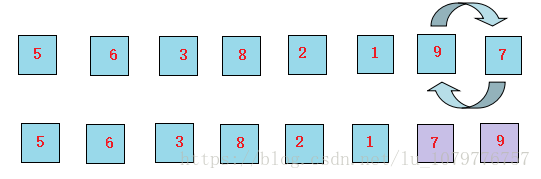
7、最后,让9和7交换位置
这样一来,元素9作为数列的最大元素,就已经排序好了。
下面我们来进行第二轮排序:
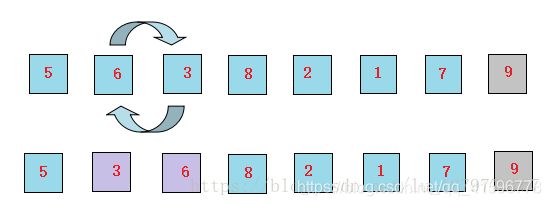
1、首先让5和6比较,发现5比6小,位置不变
2、接下来让6和3比较,发现6比3大,交换位置
3、接下来让6和8比较,6比8小,位置不变
4、8和2比较。8比2大,交换位置
5、接下来让8和1比较,8比1大,因此交换位置
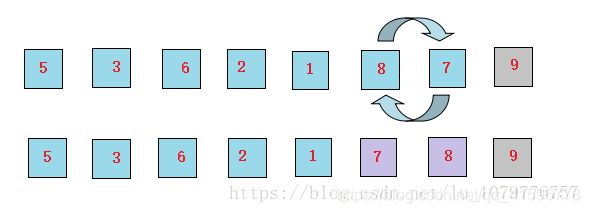
6、继续让8和7比较,发现8比7大,交换位置
第二轮的状态为:
第三轮的状态为:
第四轮的状态为:
第五轮的状态为:
第六轮的状态:
第七轮状态为:(已经有序了)
第八轮的状态为:
到此为止,所有的元素欧式有序的了,这就是冒泡排序的整体思路。
代码示例
import java.util.Arrays;
public class Demo01 {
public static void main(String[] args) {
int []a = {2, 9, 12, 31, 6};
int temp;
for(int i = 0; i < a.length - 1; i++) {
for(int j = 0; j < a.length - i - 1; j++) {
if(a[j] > a[j + 1]) {
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
System.out.print(Arrays.toString(a));
}
}选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
算法步骤
- 第一趟遍历N个数据,找出其中最小的数值与第一个元素交换
- 第二趟遍历剩下的N-1个数据,找出其中最小的数值与第二个元素交换
- 第三趟遍历剩下的N-2个数据,找出其中最小的数值与第三个元素交换
- 依次重复上述过程,直至排序完毕。
图片演示
代码示例
import java.util.Arrays;
public class Demo01 {
public static void main(String[] args) {
int []a = {4, 9, 12, 31, 6};
int temp;
for (int i = 0; i < a.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < a.length; j++) {
if (a[minIndex] > a[j]) {
minIndex = j;
}
}
if (minIndex != i) {
temp = a[i];
a[i] = a[minIndex];
a[minIndex] = temp;
}
}
System.out.print(Arrays.toString(a));
}
}插入排序
算法步骤
1.从数组的第二个数据开始往前比较,即一开始用第二个数和他前面的一个比较,如果 符合条件(比前面的大或者小,自定义),则让他们交换位置。
2.然后再用第三个数和第二个比较,符合则交换,但是此处还得继续往前比较,比如有 5个数8,15,20,45, 17,17比45小,需要交换,但是17也比20小,也要交换,当不需 要和15交换以后,说明也不需要和15前面的数据比较了,肯定不需要交换,因为前 面的数据都是有序的。
3.重复步骤二,一直到数据全都排完。
图片演示
假设前面 n-1(其中 n>=2)个数已经是排好顺序的,现将第 n 个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。
按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
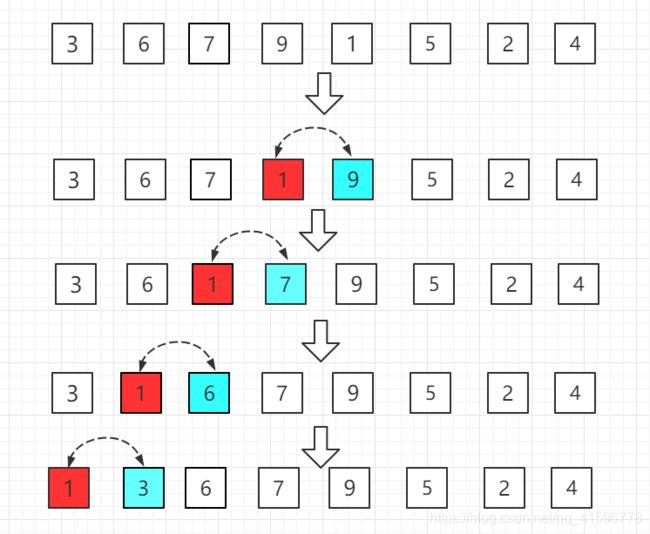
从小到大的插入排序整个过程如图示:
第一轮:从第二位置的 6 开始比较,比前面 7 小,交换位置。
第二轮:第三位置的 9 比前一位置的 7 大,无需交换位置。
第三轮:第四位置的 3 比前一位置的 9 小交换位置,依次往前比较。
第四轮:第五位置的 1 比前一位置的 9 小,交换位置,再依次往前比较。
......
就这样依次比较到最后一个元素。
代码示例
import java.util.Arrays;
public class Demo01 {
public static void main(String[] args) {
int []a = {4, 9, 12, 31, 6};
int insertNum;
int insertIndex;
for(int i=1;i=0 && a[insertIndex]>insertNum){
a[insertIndex+1] = a[insertIndex];
insertIndex--;
}
a[insertIndex+1] = insertNum;
}
System.out.print(Arrays.toString(a));
}
}