数据库期末
2018年数据库原理
- 一、简答题
-
-
- **为什么要在数据库中引入事务的概念?**
- **为什么要数据库的调度进行可串行化判别,其实际意义是什么?**
- **若对数据库进行BCNF范式的分解,从而导致没有保持依赖,在数据库中要如何解决**
- **数据库中,实体的完整性是如何被保证的**
- **如何降低数据可中的数据的冗余度**
- **如何标识一个弱实体集**
- **在SQL语句中,如何表示除法运算**
- **在关系代数中,与等值连接相比,自然连接的缺点是什么?**
- 二、分析题
-
- 1.如果关系r\(R\)和s(S)中不含有任何相同属性,即 R ∩ S R\cap S R∩S= ∅ \empty ∅,那么 r ∞ s = r × s r\infty s=r\times s r∞s=r×s.
- 某人在使用移动支付系统时,输入了正确的支付密码并提交后,发现了断网情况,导致支付失败,分析该事务经历了那几个状态?
- 某学校教务管理系统为每个学院提供了固定的上课教室,系统规定不同学院的教务负责人员登录本系统后,只能有权支配各自学院的教师资源,请问需要定义哪种数据库对象实现此需求?为什么?
- 某学院教务管理系统有学生表”(学号,姓名,出生日期,学员编号)“和选课信息表*(学号,课程编号,成绩)”。现有如下规定:如果某学生退学的话,则自动删除该生的所有选课记录,该如何定义此业务逻辑?
- 三、设计题
-
- 某连锁超市有若干门店,若干员工和若干商品。每个门店有若干员工和一个店长,店长负责管理本门店的所有员工,每个员工只在特定门店工作。各个门店销售的商品基本相同,由于销售差异,每个门店所拥有的特定商品的数量有所不同。
- 1.根据上述需求,画出E-R模型
- 将E-R模型转化为相应的关系模型,并说明每个关系模式必要的完整性约束。
- 四、计算题
-
- 1.设有如图所示调度S,判别S是否为冲突可串行化调度?如果是则给出与S等价的一个串行化调度,如果不是,说明为什么。
- 2.设有关系模式R=(A,B,C,D,E,G,H),F={AH → \rightarrow →C,C → \rightarrow →A,CH → \rightarrow →D,C → \rightarrow →EG,EH → \rightarrow →C,CG → \rightarrow →DH,CE → \rightarrow →AG,ACD → \rightarrow →H}
-
- 1)令X=BC,求X关于F的闭包
-
- 2)将关系R逐渐分解为3NF
- 五、应用题
-
- 2、分别用关系代数和SQL语句查询;下载数量超过500此的游戏名称
- 3、分别用关系代数和SQL语句查询;下载了游戏'G01'没下载‘G02’的玩家姓名。
- 4 、用关系代数完成查询;查询下载了所有益智类游戏的玩家id
- 5、用SQL语句完成查询;查询年龄15-25岁的玩家都下载了那些游戏?
- 6、用户p01下载了游戏G02,在数据库中应当发送的SQL语句是什么?
- 7、用SQL语句完成,游戏开发者修改了游戏后重新上传,版本号发生了变化,数据库完成了什么操作。
-
一、简答题
为什么要在数据库中引入事务的概念?
要在数据库并发控制下保持数据库的一致性。
为什么要数据库的调度进行可串行化判别,其实际意义是什么?
通过保证所执行的调度的效果与没有并发执行的调度效果一样,可以确保数据库的一致性。
若对数据库进行BCNF范式的分解,从而导致没有保持依赖,在数据库中要如何解决
改为第三范式分解
数据库中,实体的完整性是如何被保证的
not null,unique,check,参照完整性。
如何降低数据可中的数据的冗余度
设计选择:更小的模式
如何标识一个弱实体集
没有足够的属性以形成主码的实体集称作弱实体集,在E-R图中弱实体集的分辨符以虚下划线标明
在SQL语句中,如何表示除法运算
利用Where子句,A/B,表示为 not exists(B except A)
在关系代数中,与等值连接相比,自然连接的缺点是什么?
自然连接是在笛卡尔积的基础上保留相同属性下取值相同的元组,而等值连接可以在笛卡尔积的基础上自由选择比较的属性。
二、分析题
1.如果关系r(R)和s(S)中不含有任何相同属性,即 R ∩ S R\cap S R∩S= ∅ \empty ∅,那么 r ∞ s = r × s r\infty s=r\times s r∞s=r×s.
由于r和s的自然连接是在迪克尔积的基础上进行相同属性的取值相同进行筛选元组,所以没有相同的属性就不用删除元组了,所以最终结果和笛卡尔积记过一样。
某人在使用移动支付系统时,输入了正确的支付密码并提交后,发现了断网情况,导致支付失败,分析该事务经历了那几个状态?
活动状态 → \rightarrow →部分提交状态 → \rightarrow →失败状态 → \rightarrow →中止
某学校教务管理系统为每个学院提供了固定的上课教室,系统规定不同学院的教务负责人员登录本系统后,只能有权支配各自学院的教师资源,请问需要定义哪种数据库对象实现此需求?为什么?
学校教务管理系统首先创建每个学院单独的视图,然后将对应学院的视图的权限赋给对应的教务负责人。
某学院教务管理系统有学生表”(学号,姓名,出生日期,学员编号)“和选课信息表*(学号,课程编号,成绩)”。现有如下规定:如果某学生退学的话,则自动删除该生的所有选课记录,该如何定义此业务逻辑?
利用触发器,触发事件是delete from 学生 where 学号=“***”;然后就删除选课信息表中学号是退学学生的学号的元组。
三、设计题
某连锁超市有若干门店,若干员工和若干商品。每个门店有若干员工和一个店长,店长负责管理本门店的所有员工,每个员工只在特定门店工作。各个门店销售的商品基本相同,由于销售差异,每个门店所拥有的特定商品的数量有所不同。
1.根据上述需求,画出E-R模型
将E-R模型转化为相应的关系模型,并说明每个关系模式必要的完整性约束。
门店( 门 店 编 号 ‾ \underline{门店编号} 门店编号,名字,地址)
员工( 员 工 编 号 ‾ \underline{员工编号} 员工编号,员工名字,员工电话,工资)
商品( 商 品 编 号 ‾ \underline{商品编号} 商品编号,商品名字)
拥有( 门 店 编 号 ‾ \underline{门店编号} 门店编号, 商 品 编 号 ‾ \underline{商品编号} 商品编号, 数 量 ‾ \underline{数量} 数量)门店编号是参照关系门店的外码,商品编号是参照关系商品的外码。
工作( 员 工 编 号 ‾ \underline{员工编号} 员工编号,门店编号)门店编号是参照关系门店的外码
管理( 普 通 员 工 ‾ \underline{普通员工} 普通员工,店长)店长是参照关系员工的外码
四、计算题
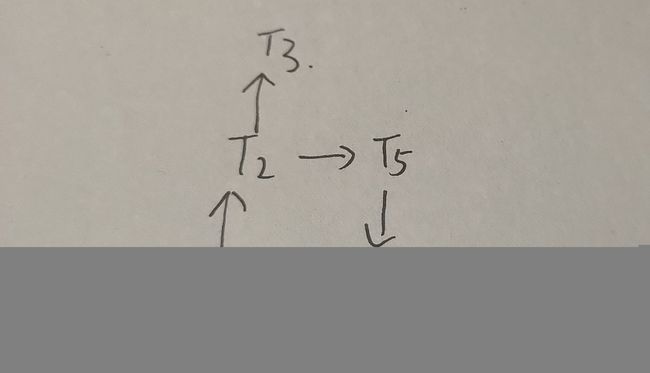
1.设有如图所示调度S,判别S是否为冲突可串行化调度?如果是则给出与S等价的一个串行化调度,如果不是,说明为什么。
不是,因为T2,T5,T4,T1形成了一个环。
2.设有关系模式R=(A,B,C,D,E,G,H),F={AH → \rightarrow →C,C → \rightarrow →A,CH → \rightarrow →D,C → \rightarrow →EG,EH → \rightarrow →C,CG → \rightarrow →DH,CE → \rightarrow →AG,ACD → \rightarrow →H}
1)令X=BC,求X关于F的闭包
B,C,A,E,G,D,H
2)将关系R逐渐分解为3NF
R的正则覆盖为Fc={AH → \rightarrow →C,C → \rightarrow →ADEGH,EH → \rightarrow →C}
分解的3NF是:
(A,C,H),(A,C,D,E,G,H),(E,H,C)
由于(A,C,H)包含在(A,C,D,E,G,H)所以可以删除(A,C,H)
没有候选码(B,C)所以再增加一个模式(B,C)
综上所述为:
(A,C,D,E,G,H)
(E,H,C)
(B,C)
五、应用题
###1、分别用关系模式和SQL语句查询;玩家“wxy"下载的所有游戏的名称。
select Gname
from (PERSON natural join PG) natural join GAME
where Pname='wxy';
∏ G n a m e ( σ P n a m e = ′ w x y ′ ( G A M E ∞ P E R S O N ∞ P G ) ) \begin{matrix} \prod_{Gname}\end{matrix}(\sigma_{Pname='wxy'}(GAME\infty PERSON \infty PG)) ∏Gname(σPname=′wxy′(GAME∞PERSON∞PG))
2、分别用关系代数和SQL语句查询;下载数量超过500此的游戏名称
select Gname,count(Pid)
from GAME natural join PG
group by Gname
having count(Pid)>500
∏ G n a m e ( σ c _ p i d > 500 ( ρ c o u n t g a m e ( G n a m e , c _ p i d ) ( ( G n a m e ) g c o u n t ( P i d ) ( G A M E ∞ P G ) ) ) ) \begin{matrix} \prod_{Gname}\end{matrix}(\sigma_{c\_pid>500}(\rho_{countgame(Gname,c\_pid)}((Gname)g_{count(Pid)}(GAME \infty PG)))) ∏Gname(σc_pid>500(ρcountgame(Gname,c_pid)((Gname)gcount(Pid)(GAME∞PG))))
3、分别用关系代数和SQL语句查询;下载了游戏’G01’没下载‘G02’的玩家姓名。
(select distinct Pname
from PERSON natural join PG
where Gid='G01')
except
(
select distinct Pname
from PERSON natural join PG
where Gid='G02'
);
∏ P n a m e ( σ G i d = ′ G 0 1 ′ ( P E R S O N ∞ P G ) − ∏ P n a m e ( σ G i d = ′ G 0 2 ′ ( P E R S O N ∞ P G ) ) \begin{matrix} \prod_{Pname}\end{matrix}(\sigma_{Gid='G01'}(PERSON \infty PG)-\begin{matrix} \prod_{Pname}\end{matrix}(\sigma_{Gid='G02'}(PERSON \infty PG)) ∏Pname(σGid=′G01′(PERSON∞PG)−∏Pname(σGid=′G02′(PERSON∞PG))
4 、用关系代数完成查询;查询下载了所有益智类游戏的玩家id
∏ P i d , G i d ( P G ) ÷ ∏ G i d ( σ t y p e = ′ 益 智 类 ′ ( G A M E ) ) \begin{matrix} \prod_{Pid,Gid}\end{matrix}(PG) \div \begin{matrix} \prod_{Gid}\end{matrix}(\sigma_{type='益智类'}(GAME)) ∏Pid,Gid(PG)÷∏Gid(σtype=′益智类′(GAME))
5、用SQL语句完成查询;查询年龄15-25岁的玩家都下载了那些游戏?
select GAME
from PERSON natural join PG natural join GAME
where age>=15 and age<=25;
6、用户p01下载了游戏G02,在数据库中应当发送的SQL语句是什么?
insert into PG values ({'p01','G02'});
7、用SQL语句完成,游戏开发者修改了游戏后重新上传,版本号发生了变化,数据库完成了什么操作。
利用update更新操作。
update GAME
set type=' '
where Gid=' ';