良人从零开始的踩坑笔记:浮点数
浮点数,真的很难学
- 什么是浮点数
-
- 浮点数的存储标准:IEEE754
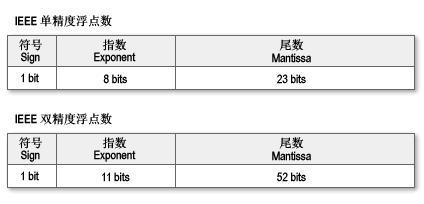
- 浮点数的数学表示:Sign,Exponent和Significand
- 浮点数的数据类型:float与double
- 浮点数的数值范围
-
- float的取值范围
- double的取值范围
- 浮点数的特殊取值
- 浮点数与其他数制的转换
- 浮点数运算
-
- 五种异常情况
- 浮点数加法
-
- 1.对阶
- 2.尾数加减
- 3.尾数规格化
- 4.舍入
- 5.校验
因为我上课没好好听
什么是浮点数
浮点数,是与定点数相对的概念,指小数点位置约定在固定位置的数。
浮点数的存储标准:IEEE754
浮点数在计算机中以遵循IEEE754浮点数计数标准的方式存储。
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现)。
浮点数的数学表示:Sign,Exponent和Significand
X = ( − 1 ) S × M × R E X=(-1)^{S}\times M\times R^{E} X=(−1)S×M×RE
S,Sign:符号位,决定该浮点数的正负
M,Mantissa/Significand:尾数,取值为[1,2)的二进制小数。
R,Radix base:基数,对浮点数加权,权重为2的E次幂。
E,Exponent:阶/指数,二进制定点(无符号)整数。
考试的时候问你尾数是什么,你要回答小数点后那部分
在基数R一定的情况下:
尾数M的位数反映数X的有效位数,它决定了数的表示精度,有效位数越多,表示精度越高。
阶E的位数决定数X的表示范围,值确定了小数点的位置。
M位数越多,X越精确。
E越大,X越大
浮点数的数据类型:float与double
IEEE754规定浮点数有单精确度、双精确度、延伸单精确度与延伸双精确度四种类型,但是本文只对单精确度float与双精确度double类型作分析学习。
在科学计数法中指数是可以取负数的,所以IEEE754规定计算机存储浮点数时,阶E需要在真实值基础上再减去一个偏移值bias,即127(for float)或1023(for double)
M的取值为[1,2),即M可写为1.xxxx的形式,xxxx越长浮点数越精确。
规格化尾数M的小数点后第一位总是1,故规定第一位默认的1被省略,由此用23个数表示24位尾数。
浮点数的数值范围
绝对值范围为:
2 − ( 2 e − 1 ) × 2 − m ≤ ∣ X ∣ ≤ ( 1 − 2 − m ) × 2 ( 2 m − 1 ) 2^{-(2^{e}-1)} \times 2^{-m} \leq \left | X \right |\leq (1-2^{-m}) \times 2^{(2^{m}-1)} 2−(2e−1)×2−m≤∣X∣≤(1−2−m)×2(2m−1)
其中e和m分别表示阶数与尾数的位数
float的取值范围
在32位浮点数中,符号位占1位,尾数占23位,阶数占8位。
不考虑阶数全为0或全为1的情况下,8位二进制数取值范围即[1,254]减去其偏移量127,得到阶数的规格化范围为 [-126,127]。
在正常情况下,阶数不包括全为0或全为1的情况
实际的指数值 -127(保存为全0)以及 +128(保存为全 1)保留用作特殊值(见下文)
正数最小值为
| Sign | Exponent | Mantissa |
|---|---|---|
| 0 | 00000001 | 00000000000000000000000 |
1.00...0 × 2 00...1 = 1 × 2 − 126 = 2 − 126 1.00...0 \times 2^{00...1}=1 \times 2^{-126}=2^{-126} 1.00...0×200...1=1×2−126=2−126
正数最大值为
| Sign | Exponent | Mantissa |
|---|---|---|
| 0 | 11111110 | 11111111111111111111111 |
1.11...1 × 2 11111110 = ( 2 − 2 − 23 ) × 2 127 ≈ 3.4028234664 × 1 0 38 1.11...1 \times 2^{11111110}=(2-2^{-23}) \times 2^{127} \approx 3.4028234664 \times 10^{38} 1.11...1×211111110=(2−2−23)×2127≈3.4028234664×1038
于是对于正浮点数有:
1.0 × 2 − 126 ≈ 1.1755 × 1 0 − 38 ≤ F l o a t N u m ≤ ( 2 − 2 − 23 ) × 2 127 ≈ 3.4028 × 1 0 38 1.0 \times 2^{-126} \approx 1.1755 \times 10^{-38} \leq FloatNum \leq (2-2^{-23}) \times 2^{127} \approx 3.4028 \times 10^{38} 1.0×2−126≈1.1755×10−38≤FloatNum≤(2−2−23)×2127≈3.4028×1038
同理对于负浮点数有
− ( 2 − 2 − 23 ) × 2 127 ≈ − 3.4028 × 1 0 38 ≤ F l o a t N u m ≤ − 1.0 × 2 − 126 ≈ − 1.1755 × 1 0 − 38 ≈ 3.4028 × 1 0 − 38 -(2-2^{-23}) \times 2^{127} \approx -3.4028 \times 10^{38} \leq FloatNum \leq -1.0 \times 2^{-126} \approx -1.1755 \times 10^{-38} \approx 3.4028 \times 10^{-38} −(2−2−23)×2127≈−3.4028×1038≤FloatNum≤−1.0×2−126≈−1.1755×10−38≈3.4028×10−38
double的取值范围
在64位浮点数中,符号位占1位,尾数占52位,阶数占11位。
不考虑阶数全为0或全为1的情况下,11位二进制数取值范围即[1,2046]减去其偏移量1023,得到阶数的规格化范围为 [-1022,1023]。
实际的指数值 -1023(保存为全0)以及 +1024(保存为全 1)保留用作特殊值
正数最小值为
| Sign | Exponent | Mantissa |
|---|---|---|
| 0 | 00000000001 | 0000000000000000000000000000000000000000000000000000 |
1.00...0 × 2 00...1 = 1 × 2 − 1022 = 2 − 1022 1.00...0 \times 2^{00...1}=1 \times 2^{-1022}=2^{-1022} 1.00...0×200...1=1×2−1022=2−1022
正数最大值为
| Sign | Exponent | Mantissa |
|---|---|---|
| 0 | 11111111110 | 1111111111111111111111111111111111111111111111111111 |
1.11...1 × 2 11...10 = ( 2 − 2 − 52 ) × 2 1023 ≈ 1.7976931348623157 × 1 0 308 1.11...1 \times 2^{11...10}=(2-2^{-52}) \times 2^{1023} \approx 1.7976931348623157 \times 10^{308} 1.11...1×211...10=(2−2−52)×21023≈1.7976931348623157×10308
于是对于正浮点数有:
1.0 × 2 − 1022 ≈ 2.2251 × 1 0 − 308 ≤ D o u b l e N u m ≤ ( 2 − 2 − 52 ) × 2 1023 ≈ 1.7977 × 1 0 308 1.0 \times 2^{-1022} \approx 2.2251 \times 10^{-308} \leq DoubleNum \leq (2-2^{-52}) \times 2^{1023} \approx 1.7977 \times 10^{308} 1.0×2−1022≈2.2251×10−308≤DoubleNum≤(2−2−52)×21023≈1.7977×10308
同理对于负浮点数有
− ( 2 − 2 − 52 ) × 2 1023 ≈ − 1.7977 × 1 0 308 ≤ D o u b l e N u m ≤ − 1.0 × 2 − 1022 ≈ − 2.2251 × 1 0 − 308 -(2-2^{-52}) \times 2^{1023} \approx -1.7977 \times 10^{308} \leq DoubleNum \leq -1.0 \times 2^{-1022} \approx -2.2251 \times 10^{-308} −(2−2−52)×21023≈−1.7977×10308≤DoubleNum≤−1.0×2−1022≈−2.2251×10−308
浮点数的特殊取值
Single-precision floating-point format:
https://en.wikipedia.org/wiki/Single-precision_floating-point_format
Double-precision floating-point format:
https://en.wikipedia.org/wiki/Double-precision_floating-point_format
这里贴一个小工具,在IEEE754的标准下手动控制输入Sign,Exponent和Mantissa的值,输出对应的十进制值,二进制值,十六进制值,非常简单直观
https://www.h-schmidt.net/FloatConverter/IEEE754.html
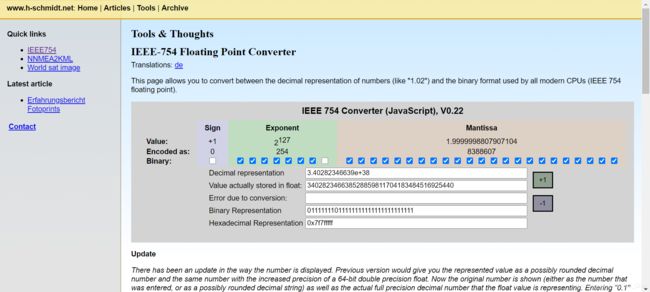
常见浮点数特殊值取值如下表
| Sign | Exponent | Mantissa | |
|---|---|---|---|
| 0 | Both cases valid | all zeros | all zeros |
| + ∞ +\infty +∞ | zero | all ones | all zeros |
| − ∞ -\infty −∞ | one | all ones | all zeros |
| NaN | Both cases valid | all ones | nonzero |
| Denorms | Both cases valid | all zeros | nonzero |
更多特殊值见上floating-point format from Wikipedia
浮点数与其他数制的转换
将十进制数-0.75转换为IEEE754的单精度浮点数格式表示
(-0.75) 10 = (-0.11) 2 = (-1.1) 2 × 2-1 = (-1)s × 1.f × 2e-127
s = 1,f = 0.100…0,e = (127-1) 10 = ( 01111 1110 ) 2 ,表示为单精度浮点数格式为 1 0111 1110 1000 0000…0000 000,用十六进制表示为BF40 0000H
求IEEE754单精度浮点数C0A0 0000H的值是多少
将C0A0 0000H展开为一个32位单精度浮点数:1 10000001 010 0000…0000.
s = 1,f = (0.01) 2 = (0.25) 10 ,阶码e = (10000001) 2 = (129)10
所以其值为( -1 )s × 1.f × 2e-127 = (-1)1 × 1.25 × 2129-127 = -1.25 × 22 = -5.0
浮点数运算
五种异常情况
1.无效运算(无意义)
-运算时有一个数是非有限数,如:
加/减 ∞,0 × ∞,∞ / ∞等
-结果无效,如:
源操作数是NaN、0 / 0、x REM 0、∞ REM y等
2.除以0
结果即无限大
3.阶上溢
对于float,指阶码exponent > 1111 1110,即大于127
4.阶下溢
对于float,指阶码exponent < 0000 0001,即小于-126
5.结果不精确
舍入时引起的异常,如1/3、1/10等不能精确表示为浮点数
浮点数加法
设Xm、Ym分别是X和Y的尾数,Xe、Ye分别是X和Y的阶码
1.对阶
对阶的目的是使两数阶码相等
小阶向大阶看齐,阶码小的数的尾数向右移,右移位数等于两个阶码差的绝对值Δe = Ye - Xe。
IEEE754尾数右移时,要将隐藏的“1”移到小数部分,高位补0,移出的低位保留到特定的“附加位”上
2.尾数加减
Xm × 2^(Xe-Ye) ± Ym
3.尾数规格化
当尾数高位为0,则需左规:尾数左移一次,阶码减一,直到MSB(阶码最高位)为1
每次阶码减一后要判断阶码是否下溢,阶码下溢则结果为0
当尾数最高位有进位,则需右规:尾数右移一次,阶码加一,直到MSB为1
每次阶码加一后要判断阶码是否上溢,阶码上溢则结果溢出
右规最多只需要一次,因为即使是最大的两个尾数相加(1.11…1+1.11…1),其结果也不会达到4,故尾数的整数部分最多有2位,保留一个隐含的"1"后,最多只有一位被右移到小数部分
4.舍入
如果尾数比规定数位长(有附加位),则需考虑舍入(舍入的方式有多种)
没写完,等我考完试
5.校验
若运算结果尾数为0,则说明结果为0,即阶码和尾数均应为0,需要将阶码也置0.
用二进制浮点数形式计算0.5 +(-0.4375)的值
(0.5)10 = 1.000 × 2-1(大阶),(-0.4375) = -1.110 × 2-2(小阶)
对阶: -1.110 × 2-2 → 0.111 × 2-1
加减: 1.000 × 2-1 + (-0.111 × 2-1) = 0.001 × 2-1
左规: 0.001 × 2-1 → 1.000 × 2-4
判断溢出:否
所以结果为1.000 × 2-4 = 0.0001000 = 1/16 = 0.0625

