用图讲解狄克斯特拉（DiskStra）算法，python实现 。

最短路径

在一个带权图中，顶点V0到图中任意一个顶点Vi的一条路径所经过边上的权值之和，定义为该路径的带权路径长度，把带权路径最短的那条路径称为最短路径。
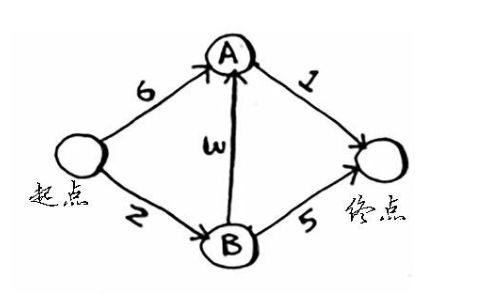
如图所示，求双子峰到金门大桥的最短距离。

此类问题要用到狄克斯特拉（DiskStra）算法

使用狄克斯特拉（DiskStra）算法

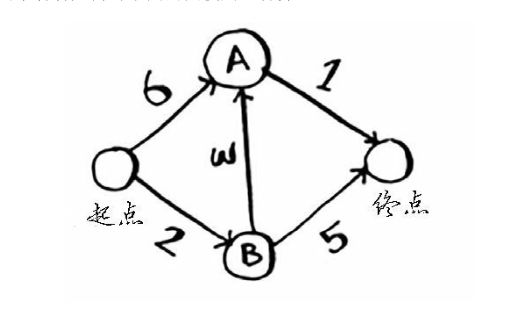图中每个数字都是时间，为此找出从起点到终点用时最短的路径。

如果你使用广度优先搜索，广度优先搜索算法BFS讲解以及python 实现
你将得到下面这条段数最少的路径。

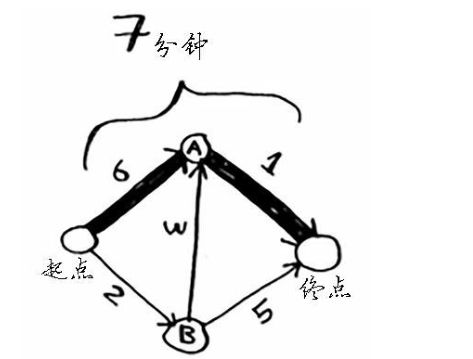
这条路径耗费7分钟，我们接下来找找还有没有更短的路径。
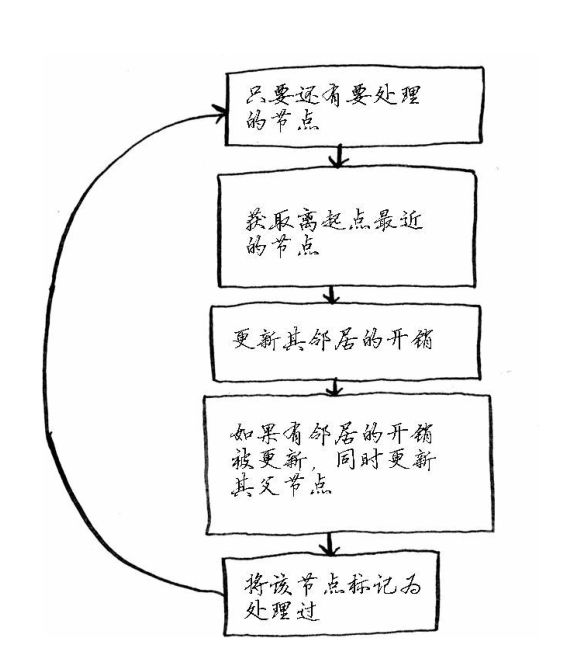
狄克斯特拉（DiskStra）算法 包含4个步骤：

1. 找出可在最短时间内到达的点
2. 更新该节点的邻居的开销
3. 重复计算该过程，直到对所有节点都做了
4. 计算最终路径

第一步：你站在起点，可以走的点是A，B。到达A需要6分钟，到达B需要2分钟，其他节点不能到达，设为无穷。

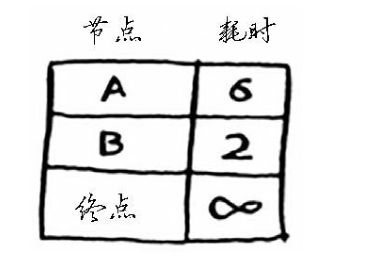
第二步：因为起点到B最近，然后计算B前往各邻居的距离
B到A的距离是3，我们找到一条前往A点的更短路径5，从起点直接前往A点距离是6，则更新库中起点到A的距离。

对于节点B的邻居，如果找到前往它的更短路径，就更新其开销，在这里我们找到了：前往A点的更短路径，时间由6分钟缩短到了5分钟；前往终点的更短路径，时间由无穷大缩短到7分钟。

第三步：重复
重复第一步,找出最短时间可以到达的点，前面对节点B执行了第二步，除B点外，还有节点A

重读第二步，更新节点A所有邻居的开销

你发现前往终点的时间为6分钟。

对每个节点都应用狄克斯特拉（DiskStra）算法，现在知道前往B节点2分钟，A分钟，终点6分钟。

狄克斯特拉（DiskStra）算法适用于有向无环图。

算例实现

以图为例

第一步：解决这个问题，需要准备三个散列表

第一个散列表表示图，依次是父节点，子节点，权重。第一个散列表图可以用散列表嵌套表示。

"""     、、、、、、  第一个散列表  用于表示图   、、、、、、     """
graph={
     }
#起点 到各邻居的关系
graph["start"]={
     }
graph["start"]["a"]=6
graph["start"]["b"]=2
#print(graph["start"].keys())#dict_keys(['a', 'b'])
#节点a到各邻居关系
graph["a"]={
     }
graph["a"]["fin"]=1

#节点b到各邻居关系
graph["b"]={
     }
graph["b"]["a"]=3
graph["b"]["fin"]=5

#终点与各邻居关系
graph["fin"]={
     }#终点没有邻居

第二个散列表为初始时起点出发到各节点的距离，随着算法进行需要不断更新。

""" 第二个散列表 节点的开销。节点的开销表示起点出发到该节点需要多少时间"""
infinity=float("inf")#无穷大
costs={
     }
costs['a']=6
costs['b']=2
costs['fin']=infinity

第三个散列表。左边为子节点，右边为父节点，用来表示路径。随着算法进行需要不断更新，是针对出发点建立的

""" 第三个散列表 存储 路径 . parents['a']="start"表示节点a的上一节点是start,如果后面发现更短路径，可以修改为parents['a']=b"""
parents={
     }
parents['a']="start"
parents['b']="start"
parents['fin']=None#出发点不能直接到达

第二步：需要一个数组，存储已经处理过的节点

"""                        需要一个数组，存储已经处理过的节点 """
processed=[]

第三步：最小开销节点函数

"""                        开销最小的函数 """
def find_lowest_cost_node(costs):
    lowest_cost=float('inf')
    lowest_cost_node=None
    for node in costs:#遍历每个节点
        cost=costs[node]
        if cost<lowest_cost and node not in processed:#如果当前节点小于最小开销，且没有处理过
            lowest_cost_node=node #则将该节点设为最小开销节点
            lowest_cost=cost#更新最小开销
    return lowest_cost_node

第四步：DiskStra算法

""" DiskStra算法"""
node=find_lowest_cost_node(costs) #在未处理的节点中找到开销最小的节点，即离出发点最近的点
while node  is not None: #这个循环表示所有节点处理过才会结束
    cost=costs[node]
    neighbors=graph[node]
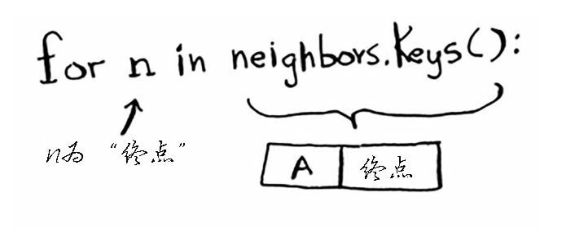
    for n in neighbors.keys():#遍历当前节点的所有邻居
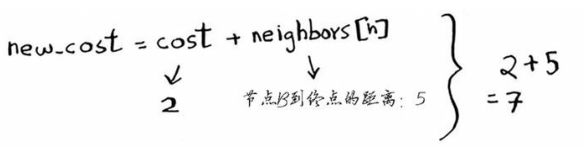
        new_cost=cost+neighbors[n]
        if costs[n]>new_cost:#如果经当前节点离该邻居更近
            costs[n]=new_cost#就更新该节点的开销
            parents[n]=node #同时将该邻居的父节点设置为该节点
    processed.append(node)#将该节点标记为处理过
    node=find_lowest_cost_node(costs) #查找接下来要循环处理的点，并循环

全部代码

"""       第一个散列表  用于表示图        """
graph={
     }
#起点 到各邻居的关系
graph["start"]={
     }
graph["start"]["a"]=6
graph["start"]["b"]=2
#print(graph["start"].keys())#dict_keys(['a', 'b'])
#节点a到各邻居关系
graph["a"]={
     }
graph["a"]["fin"]=1

#节点b到各邻居关系
graph["b"]={
     }
graph["b"]["a"]=3
graph["b"]["fin"]=5

#终点与各邻居关系
graph["fin"]={
     }#终点没有邻居

""" 第二个散列表 节点的开销。节点的开销表示起点出发到该节点需要多少时间，每个节点都要列出来"""
infinity=float("inf")#无穷大
costs={
     }
costs['a']=6
costs['b']=2
costs['fin']=infinity

""" 第三个散列表 存储 路径 . parents['a']="start"表示节点a的上一节点是start,如果后面发现更短路径，可以修改为parents['a']=b，每个节点都要列出来"""
parents={
     }
parents['a']="start"
parents['b']="start"
parents['fin']=None#出发点不能直接到达


"""                        需要一个数组，存储已经处理过的节点 """
processed=[]

"""                        开销最小的函数 """
def find_lowest_cost_node(costs):
    lowest_cost=float('inf')
    lowest_cost_node=None
    for node in costs:#遍历每个节点
        cost=costs[node]
        if cost<lowest_cost and node not in processed:#如果当前节点小于最小开销，且没有处理过
            lowest_cost_node=node #则将该节点设为最小开销节点
            lowest_cost=cost#更新最小开销
    return lowest_cost_node


""" DiskStra算法"""
node=find_lowest_cost_node(costs) #在未处理的节点中找到开销最小的节点，即离出发点最近的点
while node  is not None: #这个循环表示所有节点处理过才会结束
    cost=costs[node]
    neighbors=graph[node]
    for n in neighbors.keys():#遍历当前节点的所有邻居
        new_cost=cost+neighbors[n]
        if costs[n]>new_cost:#如果经当前节点离该邻居更近
            costs[n]=new_cost#就更新该节点的开销
            parents[n]=node #同时将该邻居的父节点设置为该节点
    processed.append(node)#将该节点标记为处理过
    node=find_lowest_cost_node(costs) #查找接下来要循环处理的点，并循环


#打印结果
print('costs',costs)
print('parents',parents)

流程图解

找到开销最少的点

获取该节点的开销和邻居

遍历邻居

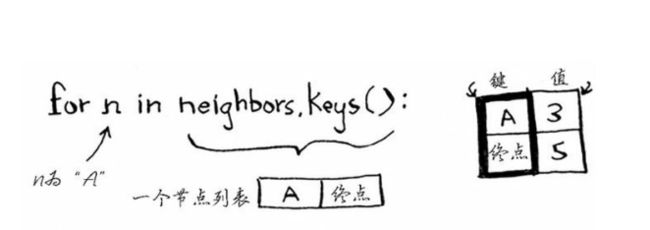
每个节点都要开销，开销指从起点到该节点需要多长时间，在这里，将计算从起点到B再到A的开销，而不是直接到A的开销

和原始开销进行对比

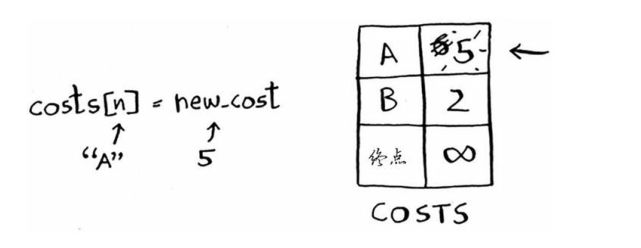
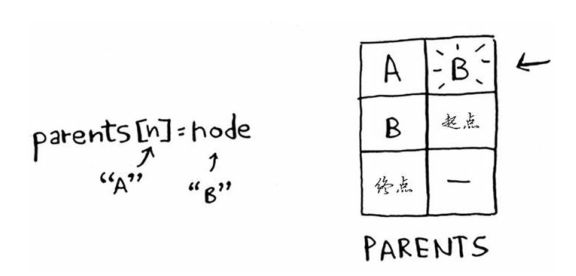
找到一条前往节点A的更短路径，更新节点A的开销 这条路径由B到A，由此更新节点A的父节点

现在回到for循环，下一个邻居是终点

经节点B前往终点需要7分钟，

原始终点节点开销为无穷大，现在7分钟，更新终点节点的开销和父节点

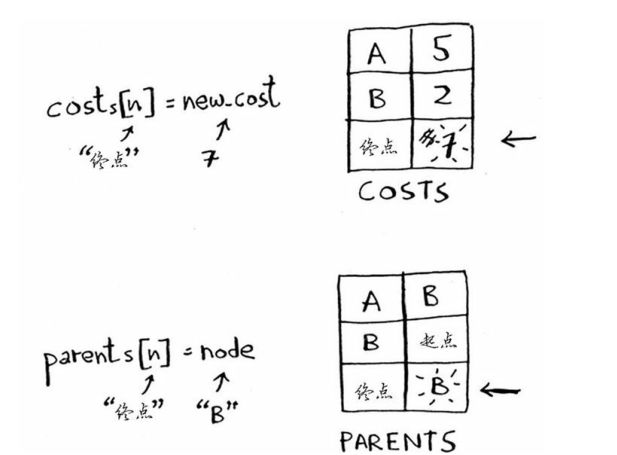
现在将节点B设为被处理过的

接下来要处理的点

获取节点A的开销和邻居

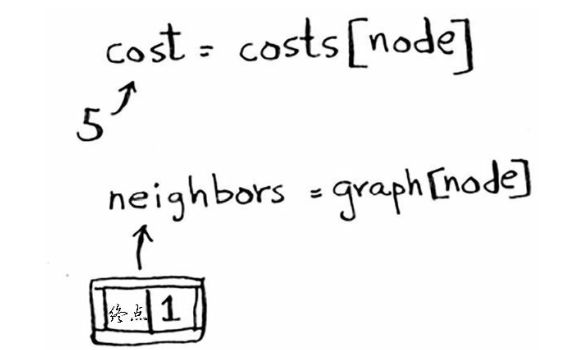
节点A只有一个邻居，终点。当前前往终点需要7分钟，经过节点A需要多久，见图

更短，更新终点的开销和父节点

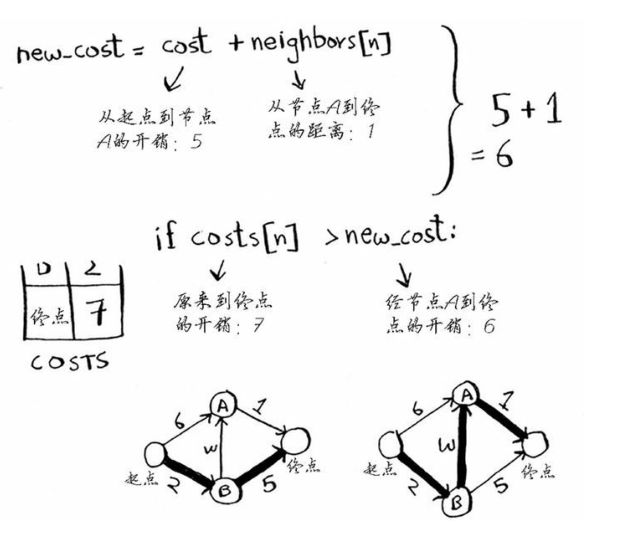
节点A被添加进处理过的。
接下来要处理的点为终点fin。
终点fin没有邻居，不更新，然后显示终点也被添加进处理过的。
node变为空，退出while循环。结束。

如果要改变起点，如起点改到A，再来探讨该问题。只需修改costs和parents散列表即可。

工具包讲解

参考我以前的博文
最短路径Dijkstra讲解，工具包使用 python


参考：《算法图解》。本文是我的学习笔记。个人博文有些是学习笔记，有些是自己做的。此文为学习笔记。
作者：电气-余登武