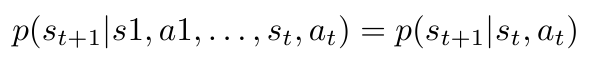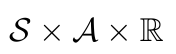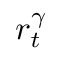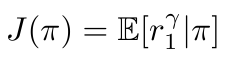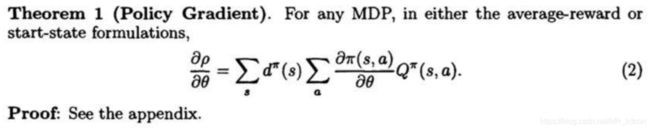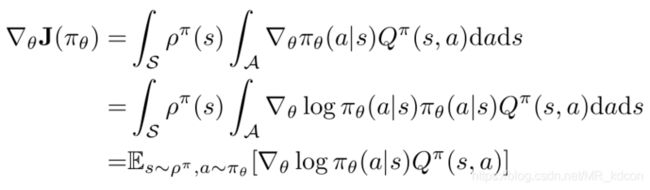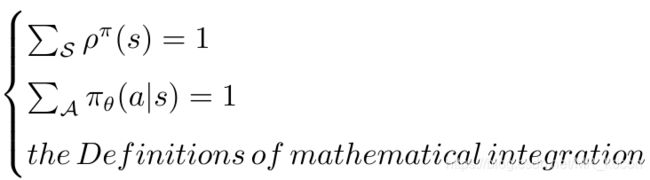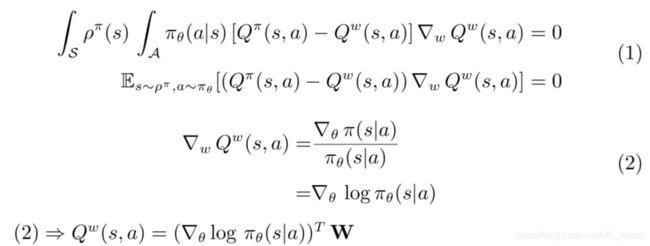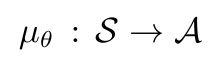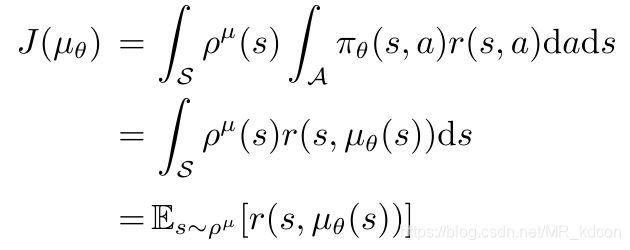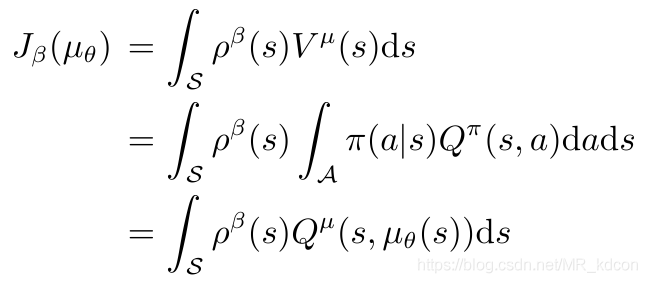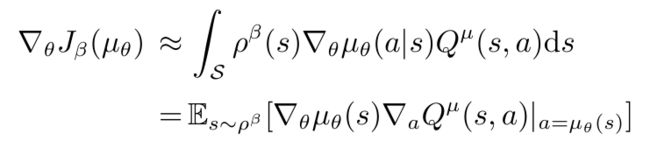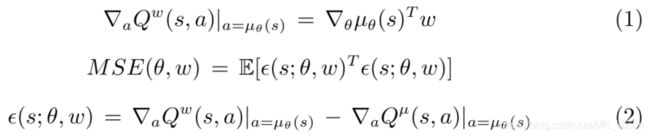Deterministic Policy Gradient Algorithms(以下简称DPG)论文笔记
Abstract：
①：作者首先指出一种叫DPG的算法用于连续动作空间的强化学习任务。与DPG相对得是随机策略梯度即Stochastic Policy Gradient(以下简称SPG)，在DPG之前，我们用高斯策略解决连续动作空间问题，用softmax策略解决离散动作空间问题，他们都是在一定概率空间内去选择动作， 而DPG是一种输出确定性策略的算法。
②：在SPG中，我们策略网络参数θ是向着期望累计奖励梯度上升的方向去更新，即
，即动作值函数梯度的期望。
③：DPG由于输出的是确定性策略，那么自然会损失一定的探索，而探索在RL中是避免陷入局部最小的重要方法，因此作者David Silver引入了一种off-policy Actor-Critic算法（OPDAC），Q-learning就是一种典型的off-policy算法，OPDAC仿照Q-learning的思想，从随机探索的行为策略中学习目标确定性策略。
④：作者最后提出DPG在高维空间中可以表现得比SPG更好！
1、Introduction
SPG广泛用于连续动作空间的RL问题（当然离散空间也可用），SPG对参数为θ策略网络的输出分布中中随机选取动作action。网路输出分布为：。
可以是softmax或者高斯策略。策略参数θ的更新是沿着期望累计奖励梯度的方向。
DPG网络输出的为一个确定的action：
，其网络参数θ的更新沿着动作值函数的梯度的方向。
此外，作者还证明了DPG是SPG的特殊情况，即当SPG的策略方差趋于0的时候，SPG就是DPG。
在随机策略梯度SPG中，我们需要对状态、动作同时积分：
，然后需要对状态和动作在相应分布下采样，当维度很高的时候，采样量就会随着增大，换句话说，SPG需要有足够的采样量才能正确输出正确的策略分布来选择正确的动作，一旦动作维度很高，那么花费的工作量还是很大的。
但是作者引入的DPG只需要对状态求积分，少了对动作的积分，即不用对动作大量的采样，提升了效率。
2、Background
2.1、Preliminaries
强化学习的任务建立在Agent在随机的环境中与环境交流随机选择动作，从而在产生的一串串时间步组成的序列中最大化期望累计奖励。
我们将强化学习的任务建立在马尔科夫决策模型上，即MDP，MDP由状态空间
。
MDP需要满足马尔科夫性质：
。
基于MDP会形成一串串轨迹
。
。
状态值函数
。
RL的目标就是最大化从初始状态开始的期望累计奖励
。
目标函数可以选择V或者Q都行，value-based就是在对最大的Q值扣出相应的动作作为最优策略。而policy-based绕开了中间那步求估计值函数并求最大值函数的过程，直接去寻找最优策略。
接下来作者定义从状态s到状态s'，经历t步的转移概率为
。
Note:
1、
是在策略π下访问过的折扣状态分布，因为策略是随机的，所以每次的状态分布都是动态变化的，因此其是一个分布。
2、r(s,a)是奖励函数。
2.2、Stochastic Policy Gradient Theorem
SPG最基本的思想就是，既然我的目标是最大化目标函数，那么就直接调整策略参数往目标函数梯度
的方向去（梯度的方向就是变化率大的方向），即梯度上升，得到了调整后的策略网络的参数，那么就相当于得到了最优策略。
Sutton在1999年发表了_policy gradient theorem_：在论文Policy gradient methods for reinforcement learning with function approximation的原理1：
和下面是等价的（
），上面是的s、a是以离散R.V表示的，对于连续的R.V：
。
这里第二步到第三步是期望的定义得来的，s和a都是随机变量，期望是由R.V的分布决定的，X属于哪个分布，就说EX是这个分布的数学期望。此外这里
。
通过
证明他两的积分为1，即可作为概率密度。
Note：
如果将公式中的
，那么就是REFORCEMENT算法，关于REFORCEMENT可以看看我的另一篇。
2.3、Stochastic Actor-Critic Algorithms
SAC算法由2部分组成，一部分策略网络Actor，另一部分是值函数网络Critic，
，可以采用TD算法去估计。
Sutton在论文Policy gradient methods for reinforcement learning with function approximation的原理2中的证明表明了若值函数近似器满足以下2个条件：
那么perfomance objective就可以改写成：
，和2.2节对比，就是用值函数近似器代替了Q真值。
从条件1中可以看出，Critic网路通过TD算法可以实现条件(1)，基于Q表的TD算法采用软更新近似Q真实值。基于nn的TD算法采用最小化二乘误差的方法近似Q值，常见的值函数近似器有nn、线性拟合等。从条件(2)可以看出，值函数近似器是关于
的线性函数。
值函数近似本来是会引入bias的，当满足上述2个条件后，值函数近似器
代替Q真值将不会引入bias。
（这个地方一直有疑惑，感觉nn符合条件1没问题，但是条件2怎么去理解就不清楚了，有知道的同学麻烦指点一下）
2.4、Off-Policy Actor-Critic
off-policy算法有2个不同的策略组成，典型的off-policy就是Q-learning算法。一个是行为策略，一个是目标策略，并且
。
定义目标函数为：
对目标函数求梯度：
为重要性采样修正因子，这是off-policy特有的，关于重要性采样，可以看我的另一篇介绍重要性采样。
Off-PolicyActor-Critic(以下简称OffPAC)：
使用行为策略
去环境交流产生一串串轨迹。
Critic网络利用轨迹采样，通过V-learning
（注意这个真实值的上标是π，说明是在最终目标策略下的真实值）作为Critic。显然Critic需要IS修正因子。
Actor网络利用轨迹采样，通过
，利用随机梯度上升去调整网络参数θ。由于随机策略下需要对action采样，故也需要IS修正因子,这里和为什么V-learning需要重要性采样原理是一样的。因为如果不加这个修正因子的话，那么就不能确保说行为策略产生的动作a会使得策略网络参数θ的更新朝着正确的方向进行，注意到公式中的Critic是V。
因此Critic和Actor网络都需要修正因子，即2个IS修正因子。
3、Gradients of Deterministic Policies
（总算开始引入正题了！）
作者在3.1和3.2节分别给出了非正规和正规的导出方式。
3.1、Action-Value Gradients
在RL任务中，策略评估负责预测值函数，通常可以采用DP、MC或者TD，策略改善通常使用贪心策略，即
表示第k轮轨迹的策略，式子体现了策略的更新，注意上标这个策略还不是目标策略π，而是前往目标策略过程中的策略。
但是这种策略改善方式在离散动作空间还能使用，如果在连续的动作空间，那么你就得去找值函数的全局最大，显然是不切合实际的，因此作者提出了一种新的思路：调整策略参数θ朝着值函数Q梯度上升的方向，对于每一个遍历的状态s，都将对参数θ进行更新。考虑到状态的单步更新的程度都不同，因此会采用小批量更新，即求策略
来提高更新的稳定性。
（
表示在策略下遍历到的状态分布，由于每个轨迹遍历的状态都不一样，故他是个分布）
因此，确定性策略下策略改善的方式为：
3.2、Deterministic Policy Gradient Theorem
正式定义如下：确定性策略：
其余和随机性策略类似，目标函数performance objective：
然后给出确定性策略梯度定理：
从这个公式中我们看出：梯度只对状态积分，相比于随机性策略，对动作的积分空间大大减少，意味着无需对动作进行采样了，大大提高了效率。
3.3、Limit of the Stochastic Policy Gradient
作者证明了确定性策略梯度是随机性策略梯度的极限情况，即策略方差趋于0的时候。
4、Deterministic Actor-Critic Algorithms
确定性策略可用于on-policy算法，也可以用于off-policy算法。对于on-policy算法，我们可以采用Sarsa作为Critic，对于off-policy算法，我们可以采用Q-learning作为Critic。作者还提出了类似于随机性策略中的消除bias的2个条件。
4.1、On-Policy Deterministic Actor-Critic
确定性策略一大弊端就是输出是确定性的值，缺乏探索性，容易陷入局部最优，因此可以在输出上人为增加一点点噪声（OrnsteinUhlenbeck噪声）干扰，以体现探索性。
On-policy Deterministic Actor-Critic由2部分组成：一部分是on-policy的Critic，如Sarsa用于预测Q值，策略改善部分由Actor不断提升Q值，对于s1，能输出确定性的a1来；另一部分是Actor网络，确定性Actor网络参数的提升不再是以策略梯度与critic相乘的形式，而是朝着Q值梯度上升的方向。和随机性策略一样，我们还是用一个值函数近似器来代替Q真实值
。
2个网络参数更新如下：
Note：w和θ的更新都是单样本更新。如果像确定性策略梯度定理那样，则θ的更新就是小批量梯度上升。
4.2、Off-Policy Deterministic Actor-Critic
off-policy由2个策略组成，记
上增加一定的噪声。
定义performance objective：
Note：
1、第二步到第三步是因为目标策略π是确定性策略。因为
看成冲激函数形式。
2、确定性策略的目标函数只对状态积分
其梯度为：
确定性策略中梯度只与状态有关，不需要对动作采样，故就不需要IS修正因子了。
Off-policy Deterministic Actor-Critic：轨迹由
。另一部分是Actor，和4.1节的on-policy Deterministic AC算法一样，参数的更新沿着Q值梯度上升的方向。
2个网络参数更新如下：
由于Critic使用Q-learning，Actor使用确定性策略，其对动作不积分不采样。故两者都不需要重要性采样，不需要IS修正因子。
4.3、Compatible Function Approximation
延续随机策略的2个条件，对于确定性策略，作者也提出了2个条件：
