Java实现:HMM+维特比算法词性标注
目录
一、前言:词性标注
二、经典维特比算法(Viterbi)
三、算法实现
四、完整代码
五、效果演示:
六、总结
一、前言:词性标注
词性标注(Part-Of-Speech tagging, POS tagging),是语料库语言学中将语料库中单词的词性按其含义和上下文内容进行标记的文本数据处理技术。词性标注可以由人工或特定算法完成,使用机器学习(machine learning)方法实现词性标注是自然语言处理(NLP)的研究内容。常见的词性标注算法包括隐马尔可夫模型(Hidden Markov Model, HMM)、条件随机场(Conditional random fields, CRFs)等。
在进入本篇算法的应用和实践之前,建议学习以下两篇内容,会有更好更容易的理解。
1、隐马尔可夫模型(HMM)来龙去脉(一)(https://blog.csdn.net/Charzous/article/details/108111860)
2、隐马尔可夫模型(HMM)来龙去脉(二)(https://blog.csdn.net/Charzous/article/details/108111860)
本篇实践的目标:
除了用jieba等分词词性标注工具,不如自行写一个算法实现同样的功能,这个过程可以对理论知识更好地理解和应用。下面将详细介绍使用HMM+维特比算法实现词性标注。在给定的单词发射矩阵和词性状态转移矩阵,完成特定句子的词性标注。
二、经典维特比算法(Viterbi)
词性标注使用隐马尔可夫模型原理,结合维特比算法(Viterbi),具体算法伪代码如下:
维特比算法正是解决HMM的三个基本问题中的第二个问题:在给定的观察序列中,找出最优的隐状态序列。应用在词性标注上,就是找到概率最大化的单词的词性。
下面是对维特比算法更加容易的解释:
- 观察序列长度 T,状态个数N
- for 状态s from 1 to N:do
- //计算每个状态的概率,相当于计算第一观察值的隐状态t=1
- v[s,1] = a(0,s)*b(O1|s) //初始状态概率 * 发射概率
- //回溯保存最大概率状态
- back[s,1]=0
- //计算每个观察(词语)取各个词性的概率,保存最大者
- for from 观察序列第二个 to T do:
- for 状态s from 1 to N:do
- //当前状态由前一个状态*转移*发射(该状态/词性下词t的概率),保存最大者
- v[s,t]=max v[i,t-1]*a[i,s]*b(Ot | s)
- //保存回溯点,该点为前一个状态转移到当前状态的最大概率点
- back[s,t]=arg{1,N} max v[i,t-1]*a(i,s)
- //最后
- v[T]=max v[T]
- back[T] = arg{1,N} max v[T]
- //回溯输出隐状态序列
三、算法实现
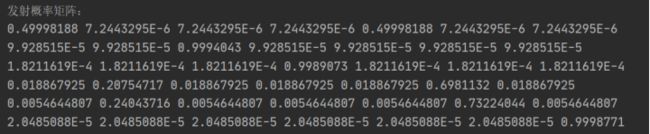
第一步,拆分算法计算问题,计算状态转移概率矩阵和符号发射概率矩阵方法:
根据给出的单词出现次数和词性状态矩阵,使用computeProp()方法计算得到发射概率矩阵和状态转移矩阵。
public void computeProp(float[][] A) {//计算概率矩阵
int i, j;
float[] t = new float[A.length];
//平滑数据,对数组每个元素值加一
for (i = 0; i < A.length; i++) {
for (j = 0; j < A[i].length; j++) {
A[i][j] += 1;
t[i] += A[i][j];
}
}
//计算当前元素在该行中的概率
for (i = 0; i < A.length; i++)
for (j = 0; j < A[i].length; j++)
A[i][j] /= t[i];
}
第二步,核心算法。本程序的关键部分是维特比算法的实现,计算得到最大概率的隐状态,然后保存最佳状态转移位置。对于每个观察值,先计算对应的可能的隐状态。
public int[] Viterbi(float[][] A, float[][] B, String[] O,double[] init) {
int back[][] = new int[A.length][O.length];
float V[][] = new float[A.length][O.length];
int i, s, k, t;
for (i = 0; i < A.length; i++) {
V[i][0] = (float) (init[i] * B[i][0]);
back[i][0] = i;
}
//计算每个观察值的取隐状态中的最大概率
for (t = 1; t < O.length; t++) {
int[][] path = new int[A.length][O.length];
//遍历每个隐状态,计算状态转移到当前状态的概率,得到最大概率状态
for (s = 0; s < A.length; s++) {
float maxSProb = -1;
int preS = 0;
for (i = 0; i < A.length; i++) {
float prob = V[i][t - 1] * A[i][s] * B[s][t];//B[s][t]为隐状态s到观察值t的发射概率
if (prob > maxSProb) {
maxSProb = prob;
preS = i;
}
}
//保存该状态的最大概率
V[s][t] = maxSProb;
//记录路径
System.arraycopy(back[preS],0,path[s],0,t);
path[s][t]=s;//最大概率状态转移记录
}
back=path;//更新最优路径
}
//回溯路径,找到最后状态
float maxP = -1;
int lastS = 0;
for (s = 0; s < A.length; s++) {
if (V[s][O.length - 1] > maxP) {
maxP = V[s][O.length - 1];
lastS = s;
}
}
return back[lastS];//返回最佳路径
}以上是维特比算法,重要的代码语句解析可见注释。算法实现了将待标注句子使用维特比算法计算最大概率,得到最佳路径。
网上大部分使用了python实现该算法,python写起来简单,所以我尝试使用java实现,期间遇到了一些小问题,后来不断debug解决问题。得到正确的java编写的维特比算法。
四、完整代码
/*
* hmm_viterbi.java
* Copyright (c) 2020-10-17
* author : Charzous
* All right reserved.
*/
public class hmm_viterbi {
public int[] Viterbi(float[][] A, float[][] B, String[] O) {
int back[][] = new int[A.length][O.length];
float V[][] = new float[A.length][O.length];
double[] init = {0.2, 0.1, 0.1, 0.2, 0.3, 0.1};
int i, s, k, t;
for (i = 0; i < A.length; i++) {
V[i][0] = (float) (init[i] * B[i][0]);
back[i][0] = i;
}
//计算每个观察值的取隐状态中的最大概率
for (t = 1; t < O.length; t++) {
int[][] path = new int[A.length][O.length];
//遍历每个隐状态,计算状态转移到当前状态的最大概率
for (s = 0; s < A.length; s++) {
float maxSProb = -1;
int preS = 0;
for (i = 0; i < A.length; i++) {
float prob = V[i][t - 1] * A[i][s] * B[s][t];//B[s][t]为隐状态s到观察值t的发射概率
if (prob > maxSProb) {
maxSProb = prob;
preS = i;
}
}
//保存该状态的最大概率
V[s][t] = maxSProb;
//记录路径
System.arraycopy(back[preS],0,path[s],0,t);
path[s][t]=s;
}
back=path;
}
//回溯路径
float maxP = -1;
int lastS = 0;
for (s = 0; s < A.length; s++) {
if (V[s][O.length - 1] > maxP) {
maxP = V[s][O.length - 1];
lastS = s;
}
}
return back[lastS];
}
public void computeProp(float[][] A) {
int i, j;
float[] t = new float[A.length];
//平滑数据,对数组每个元素值加一
for (i = 0; i < A.length; i++) {
for (j = 0; j < A[i].length; j++) {
A[i][j] += 1;
t[i] += A[i][j];
}
}
//计算当前元素在该行中的概率
for (i = 0; i < A.length; i++)
for (j = 0; j < A[i].length; j++)
A[i][j] /= t[i];
System.out.println();
// for (i = 0; i < A.length; i++) {
// for (j = 0; j < A[i].length; j++)
// System.out.print(A[i][j] + " ");
// System.out.println();
// }
}
public static void main(String[] args) {
//状态转移矩阵
float A[][] = {
{0, 0, 0, 48636, 0, 19}, {1973, 0, 426, 187, 0, 38}, {43322, 0, 1325, 17314, 0, 185}, {1067, 3720, 42470, 11773, 614, 21392}, {6072, 42, 4758, 1476, 129, 1522}, {8016, 75, 4656, 1329, 954, 0}};
//发射矩阵
float B[][] = {
{0, 0, 0, 0, 0, 0, 69016, 0}, {0, 10065, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 5484, 0, 0, 0, 0}, {10, 0, 36, 0, 382, 108, 0, 0}, {43, 0, 133, 0, 0, 4, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 48809}};
int i, j;
//语料库词语
String[] word = {"bear", "is", "move", "on", "president", "progress", "the", "."};
//待标注句子
String O[] = {"The", "bear", "is", "on", "the", "move", "."};
//语料库词性
String Q[] = {"/AT ", "/BEZ ", "/IN ", "/NN ", "/VB ", "/PERIOD "};
String seq="Bear move on the president .";
String Os[]=seq.split(" ");
for (String w:O)
System.out.println(w);
float emission[][] = new float[B.length][O.length];
hmm_viterbi hmmViterbi = new hmm_viterbi();
hmmViterbi.computeProp(A);
//计算观察序列的转移矩阵
//根据待标注句子的词计算出每个单词的出现次数矩阵
for (i = 0; i < O.length; i++) {
int r = 0;
for (int t = 0; t < word.length; t++) {
if (O[i].equalsIgnoreCase(word[t]))
r = t;
}
for (j = 0; j < B.length; j++)
emission[j][i] = B[j][r];
}
hmmViterbi.computeProp(emission);
int path[];
path=hmmViterbi.Viterbi(A, emission, O);
for (i=0;i五、效果演示:
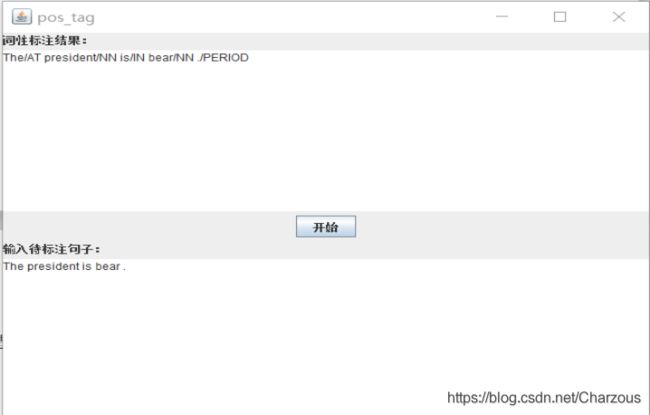
对于本实验的词性标注,简单设计了交互界面,方面测试不同句子的标注结果。在给定的测试句子”The bear is on the move .”上,实验结果如下:
The/AT bear/NN is/BEZ on/IN the/AT move/NN ./PERIOD
然后根据语料库自己造了一个句子,仅供测试用:”The president is bear .”实验结果:The/AT president/NN is/IN bear/NN ./PERIOD
感觉还可以,当然这只是一个例子,更确切需要更大的语料库。
六、总结
本篇详细介绍Java实现的HMM+维特比算法实现词性标注。在给定的单词发射矩阵和词性状态转移矩阵,完成特定句子的词性标注。这个任务可以在刚接触HMM和维特比算法进行词性标注作为实践,为之后实现特定语料库的词性标注铺垫。在完成本任务时,java编程实现算法时遇到了一些的问题,如:最佳路径的保存,回溯路径的返回。经过了一段时间的debug,实现了最基本的算法对句子进行词性标注。完成这个任务后,对HMM+Viterbi 算法的词性标注有了更深刻的理解,之后准备完成第三个任务:基于人民日报数据集的中文词性标注,可以对该算法进行更实际的应用,加深知识的理解。
我的CSDN博客:https://blog.csdn.net/Charzous/article/details/109138830