小谈Buddy System
Buddy System是一种经典的内存管理算法. 在Unix和Linux操作系统中都有用到. 其作用是减少存储空间中的空洞, 减少碎片, 增加利用率.
在Webus空间管理组件(WSM)中, 我也提供了Buddy System的实现, 关于这种算法的详细描述, 建议大家看经典教材 " 数据结构" 一书第8章第4节.
呵呵, 蓝色经典!
我在此仅谈谈如下三个问题:
1. Buddy System的基本原理?
2. 如何分配空间?
3. 如何回收空间?
对以上三个问题的说明:
Buddy System把系统中的可用存储空间划分为存储块(Block)来进行管理, 每个存储块的大小必须是2的n次幂(Pow(2, n)), 即1, 2, 4, 8, 16, 32, 64, 128...
假设系统全部可用空间为Pow(2, k), 那么在Buddy System初始化时将生成一个长度为k + 1的可用空间表List, 并将全部可用空间作为一个大小为Pow(2, k)的块挂接在List的最后一个节点上, 如下图:
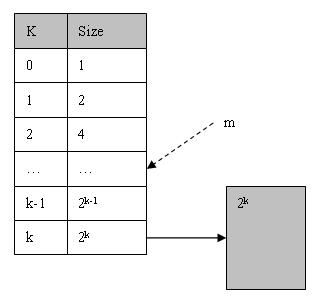
当用户申请size个字的存储空间时, Buddy System分配的Block大小为Pow(2, m)个字大小(Pow(2, m-1) < size < Pow(2, m)).
此时Buddy System将在List中的m位置寻找可用的Block. 显然List中这个位置为空, 于是Buddy System就开始寻找向上查找m+1, m+2, 直到达到k为止. 找到k后, 便得到可用Block(k), 此时Block(k)将分裂成两个大小为Pow(k-1)的块, 并将其中一个插入到List中k-1的位置, 同时对另外一个继续进行分裂. 如此以往直到得到两个大小为Pow(2, m)的块为止, 如下图所示:
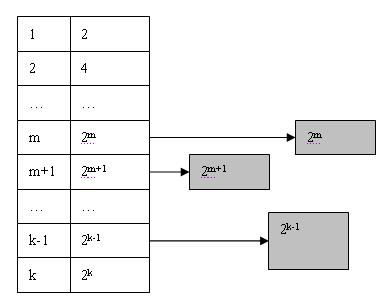
如果系统在运行一段时间之后, List中某个位置n可能会出现多个块, 则将其他块依次链接可用块链表的末尾:
当Buddy System要在n位置取可用块时, 直接从链表头取一个就行了.
当一个存储块不再使用时, 用户应该将该块归还给Buddy System. 此时系统将根据Block的大小计算出其在List中的位置, 然后插入到可用块链表的末尾. 在这一步完成后, 系统立即开始合并操作. 该操作是将"伙伴"合并到一起, 并放到List的下一个位置中, 并继续对更大的块进行合并, 直到无法合并为止.
何谓"伙伴"? 如前所述, 在分配存储块时经常会将一个大的存储块分裂成两个大小相等的小块, 那么这两个小块就称为"伙伴".在Buddy System进行合并时, 只会将互为伙伴的两个存储块合并成大块, 也就是说如果有两个存储块大小相同, 地址也相邻, 但是不是由同一个大块分裂出来的, 也不会被合并起来. 正常情况下, 起始地址为p, 大小为Pow(2, k)的存储块, 其伙伴块的起始地址为: p + Pow(2, k) 和 p - Pow(2, k).
下面把数据结构一书中Buddy算法分配存储块的C++伪码帖出来以供大家参考:
Space AllocBuddy(FreeList
&
avail,
int
n)
{
//avail[0..m]为可利用空间表, n为申请分配量, 若有不小于n的空闲块,
//则分配相应的存储块, 并返回其首地址, 否则返回NULL
for(k=0; k<=m && (avail[k].nodesize < n+1 || !avail[k].first); ++k);//查找满足分配要求的子表
if(k>m) return NULL;//分配失败, 返回NULL;
else {//可进行分配
pa = avail[k].first;//指向可分配子表的第一个节点
pre = pa->llink; suc = pa->rlink;//分配指向前驱和后继
if(pa == suc) avail[k].first = NULL;//分配后该子表变为空表
else {//从子表删除*pa节点
pre->rlink = suc; suc->llink = pre; avail[k].first = suc;
}
}
for(i = 1; avail[k-i].nodesize >= n+1; ++i) {
pi = pa + pow(2, k-i); pi-> rlink = pi; pi ->llink = pi;
pi -> tag = 0; pi -> kval = k-i; avail[k-i].first = pi;
}//将剩余块插入相应子表
pa -> tag = 1; pa -> kval = k-(--i);
return pa;
}
关于存储块回收算法, 书上没有现成的, 日后笑侃一定提供给大家, 呵呵, 今日工作繁忙, 精力不济, 要挂起了. 感谢大家的关注!
, sleeping...
相关资料:
Buddy算法认识（草稿）
Linux存储管理
Linux内存管理算法源码
在Webus空间管理组件(WSM)中, 我也提供了Buddy System的实现, 关于这种算法的详细描述, 建议大家看经典教材 " 数据结构" 一书第8章第4节.
呵呵, 蓝色经典!
我在此仅谈谈如下三个问题:
1. Buddy System的基本原理?
2. 如何分配空间?
3. 如何回收空间?
对以上三个问题的说明:
Buddy System把系统中的可用存储空间划分为存储块(Block)来进行管理, 每个存储块的大小必须是2的n次幂(Pow(2, n)), 即1, 2, 4, 8, 16, 32, 64, 128...
假设系统全部可用空间为Pow(2, k), 那么在Buddy System初始化时将生成一个长度为k + 1的可用空间表List, 并将全部可用空间作为一个大小为Pow(2, k)的块挂接在List的最后一个节点上, 如下图:
当用户申请size个字的存储空间时, Buddy System分配的Block大小为Pow(2, m)个字大小(Pow(2, m-1) < size < Pow(2, m)).
此时Buddy System将在List中的m位置寻找可用的Block. 显然List中这个位置为空, 于是Buddy System就开始寻找向上查找m+1, m+2, 直到达到k为止. 找到k后, 便得到可用Block(k), 此时Block(k)将分裂成两个大小为Pow(k-1)的块, 并将其中一个插入到List中k-1的位置, 同时对另外一个继续进行分裂. 如此以往直到得到两个大小为Pow(2, m)的块为止, 如下图所示:
如果系统在运行一段时间之后, List中某个位置n可能会出现多个块, 则将其他块依次链接可用块链表的末尾:
当Buddy System要在n位置取可用块时, 直接从链表头取一个就行了.
当一个存储块不再使用时, 用户应该将该块归还给Buddy System. 此时系统将根据Block的大小计算出其在List中的位置, 然后插入到可用块链表的末尾. 在这一步完成后, 系统立即开始合并操作. 该操作是将"伙伴"合并到一起, 并放到List的下一个位置中, 并继续对更大的块进行合并, 直到无法合并为止.
何谓"伙伴"? 如前所述, 在分配存储块时经常会将一个大的存储块分裂成两个大小相等的小块, 那么这两个小块就称为"伙伴".在Buddy System进行合并时, 只会将互为伙伴的两个存储块合并成大块, 也就是说如果有两个存储块大小相同, 地址也相邻, 但是不是由同一个大块分裂出来的, 也不会被合并起来. 正常情况下, 起始地址为p, 大小为Pow(2, k)的存储块, 其伙伴块的起始地址为: p + Pow(2, k) 和 p - Pow(2, k).
下面把数据结构一书中Buddy算法分配存储块的C++伪码帖出来以供大家参考:
Space AllocBuddy(FreeList
&
avail,
int
n)
{ //avail[0..m]为可利用空间表, n为申请分配量, 若有不小于n的空闲块, //则分配相应的存储块, 并返回其首地址, 否则返回NULL for(k=0; k<=m && (avail[k].nodesize < n+1 || !avail[k].first); ++k);//查找满足分配要求的子表 if(k>m) return NULL;//分配失败, 返回NULL; else {//可进行分配 pa = avail[k].first;//指向可分配子表的第一个节点 pre = pa->llink; suc = pa->rlink;//分配指向前驱和后继 if(pa == suc) avail[k].first = NULL;//分配后该子表变为空表 else {//从子表删除*pa节点 pre->rlink = suc; suc->llink = pre; avail[k].first = suc; } } for(i = 1; avail[k-i].nodesize >= n+1; ++i) { pi = pa + pow(2, k-i); pi-> rlink = pi; pi ->llink = pi; pi -> tag = 0; pi -> kval = k-i; avail[k-i].first = pi; }//将剩余块插入相应子表 pa -> tag = 1; pa -> kval = k-(--i); return pa;}
关于存储块回收算法, 书上没有现成的, 日后笑侃一定提供给大家, 呵呵, 今日工作繁忙, 精力不济, 要挂起了. 感谢大家的关注!
, sleeping...
相关资料:
Buddy算法认识（草稿）
Linux存储管理
Linux内存管理算法源码