数据结构与算法学习笔记
文章目录
-
- 文章介绍
- 稀疏数组学习
- 环形列队学习
- 单链表的使用与创建
- 栈的学习与字符型计算器
- 递归加八皇后问题解析
- 排序算法
-
-
-
- 冒泡排序
- 选择排序
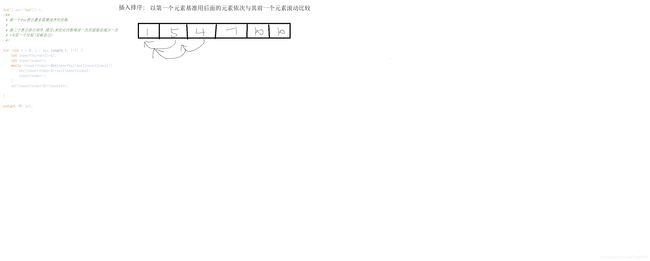
- 插入排序
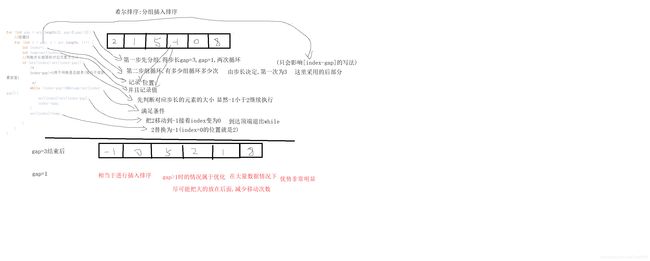
- 希尔排序(优化版插入)
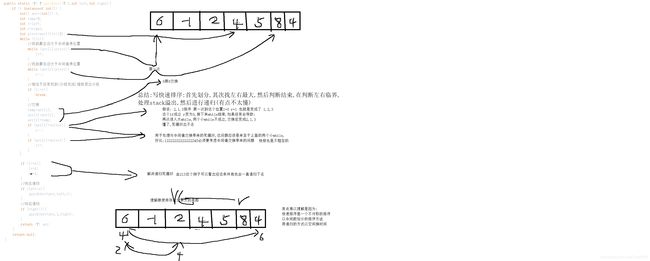
- 快速排序(分组比较递归(边分边比较))(空间换时间)
- 归并排序(递归分组比较(先分后比较))(空间换时间)
-
-
- 查找算法
-
-
-
-
- 线性查找
- 二分查找
- 二分插值查找
-
-
-
文章介绍
我将会在这篇博客中记录所有的数据结构与算法的所有学习内容
稀疏数组学习
稀疏数组就是使用n*3二维数组去更加简洁的保存数据
// An highlighted block
public class SparseArray {
public static void main() {
int[][] mapArr = new int[11][11];
mapArr[0][1] = 1;
mapArr[2][3] = 2;
int y = mapArr.length;
int x = mapArr[1].length;
int sum = 0;
for (int[] ints : mapArr) {
for (int value : ints) {
if (value > 0) {
sum++;
}
}
}
System.out.println("============================");
System.out.println(Arrays.deepToString(mapArr));
int[][] sparseArr = new int[sum + 1][3];
sparseArr[0][0] = y;
sparseArr[0][1] = x;
sparseArr[0][2] = sum;
int count = 1;
for (int i = 0; i < y; i++) {
for (int i1 = 0; i1 < x; i1++) {
if (mapArr[i][i1] > 0) {
sparseArr[count][0] = i;
sparseArr[count][1] = i1;
sparseArr[count][2] = mapArr[i][i1];
count++;
}
}
}
System.out.println(Arrays.deepToString(sparseArr));
}
}
环形列队学习
适用场景排队
public class CircleArrayQueue {
private int maxSize;//最大值
private int front;//第一个数位置
private int rear;//最后一个位置
private int[] arr;//数组
public CircleArrayQueue(int maxSize) {
this.maxSize = maxSize;
arr=new int[maxSize];
}
public boolean isFull(){
return (rear+1)%maxSize==front;
}
public boolean isEmpty(){
return front==rear;
}
public boolean addQueue(int value){
if (isFull()){
return false;
}else {
arr[rear]=value;
rear=(rear+1)%maxSize;
return true;
}
}
//front模拟>> 上移类似于消费,相当于arr[front]已被移除
public int getQueue(){
if (isEmpty()){
throw new RuntimeException("队列为空");
}
int value = arr[front];
front=(front+1)%maxSize;
return value;
}
public void showQueue(){
if (isEmpty()){
throw new RuntimeException("队列为空");
}
for (int i = front; i < front+size(); i++) {
System.out.println(i%maxSize+"AA"+arr[i%maxSize]);
}
}
public int size(){
//rear=1 front=2 maxsize =4
return (rear+maxSize-front)%maxSize;
}
public int headQueue(){
if (isEmpty()){
throw new RuntimeException("队列为空");
}else {
return arr[front];
}
}
}
单链表的使用与创建
public class MyLinkList<Type> {
//用于代理,虚拟链表
private MyNode temp;
private MyNode head = new MyNode(null);
//添加到尾部
public void add(Type o) {
temp = head;
while (true) {
if (temp.next == null) {
break;
}
temp = temp.next;
}
temp.next = new MyNode(o);
}
//定义一个按照tostring长度排序的添加规则方法
public void addOfOrder(Type o) {
temp=head;
while (true){
if (temp.next==null){
break;
}
if (temp.next.o.toString().length()>o.toString().length()){
break;
}
temp=temp.next;
}
MyNode myNode = new MyNode(o);
myNode.next=temp.next;
temp.next=myNode;
}
//修改没考虑重新排序
public boolean update(Type o,Type o2){
temp=head;
while (true){
if (temp.next==null){
return false;
}
if (temp.next.o==o){
temp.next.o=o2;
return true;
}
temp=temp.next;
}
}
//删除
public boolean delete(Type o){
temp=head;
while (true){
if (temp.next==null){
return false;
}
if (temp.next.o==o){
temp.next=temp.next.next;
return true;
}
temp=temp.next;
}
}
//获得第index个节点
public MyNode getNode(int index){
if (head.next==null||!(getLength()>index)){
return null;
}
temp=head.next;
for (int i = 0; i < index; i++) {
temp=temp.next;
}
return temp;
}
//链表反转
public boolean reverseSelf(){
//用于存储反转过程的节点
MyNode reverseTemp=new MyNode(null);
//用于记住下一个节点
MyNode reverseTempTemp;
if (getLength()<2){
return false;
}
temp=head.next;
while (true){
if (temp.next==null){
break;
}
/**
* // 举例子:
* temp=1->2->3->null
* reverseTemp.next=null
* 第一步 reverseTempTemp=2->3->null
* 第二步 temp=1->null
* 第三步 reverseTemp.next=1->null
* 第四步 temp=2->3->null
* 重复
*/
//保存temp下一个节点
reverseTempTemp=temp.next;
//当前节点的下一个变为reverseTemp的下一个,也就是说把原来已经反转或者null赋值给temp的下一个节点
// (上一步就是这不的伏笔,不然后面的节点找不到了)
temp.next=reverseTemp.next;
reverseTemp.next=temp;
temp=reverseTempTemp;
}
head.next=reverseTemp.next;
return true;
}
//使用栈反向打印
public void reversePrint(){
if (head.next==null){
return;
}
Stack<MyNode> myNodes = new Stack<>();
temp=head.next;
while (temp!= null) {
myNodes.add(temp);
temp=temp.next;
}
while (!myNodes.empty()) {
System.out.println(myNodes.pop());
}
}
//获得长度
public int getLength(){
int length=0;
temp=head;
while (temp.next != null) {
length++;
temp=temp.next;
}
return length;
}
//显示
public void showList() {
if (head.next == null) {
return;
}
temp = head.next;
while (true) {
System.out.println(temp);
temp = temp.next;
if (temp == null) {
break;
}
}
}
private class MyNode {
public Object o;
public MyNode(Object o) {
this.o = o;
}
public MyNode next;
@Override
public String toString() {
return "MyNode{" +
"o=" + o +
'}';
}
}
}
public static void main(String[] args) {
MyLinkList<String> myLinkList=new MyLinkList<String>();
myLinkList.addOfOrder("AAAA1");
myLinkList.addOfOrder("AAAA2a");
myLinkList.addOfOrder("AAAA3");
myLinkList.addOfOrder("AAAA4");
myLinkList.showList();
System.out.println("=======测试更新删除=======");
myLinkList.update("AAAA1","啊啊啊啊啊啊啊啊");
myLinkList.delete("AAAA4");
myLinkList.showList();
System.out.println("=========测试长度&&获得节点========");
System.out.println(myLinkList.getLength());
System.out.println(myLinkList.getNode(4));
System.out.println("========反转测试=========");
System.out.println(myLinkList.reverseSelf());
myLinkList.showList();
System.out.println("========使用stack反打印测试=========");
myLinkList.reversePrint();
}
打印结果
MyNode{o=AAAA1}
MyNode{o=AAAA3}
MyNode{o=AAAA4}
MyNode{o=AAAA2a}
测试更新删除
MyNode{o=啊啊啊啊啊啊啊啊}
MyNode{o=AAAA3}
MyNode{o=AAAA2a}
测试长度&&获得节点
3
null
反转测试
true
MyNode{o=AAAA3}
MyNode{o=啊啊啊啊啊啊啊啊}
使用stack反打印测试
MyNode{o=啊啊啊啊啊啊啊啊}
MyNode{o=AAAA3}
双向链表实现
public class MyDoubleLinkList<Type> {
//用于代理,虚拟链表
private MyNode temp;
private MyNode head = new MyNode(null);
//添加到尾部
public void add(Type o) {
temp = head;
while (true) {
if (temp.next == null) {
break;
}
temp = temp.next;
}
temp.next = new MyNode(o);
temp.next.pre=temp;
}
//修改没考虑重新排序
public boolean update(Type o,Type o2){
temp=head;
while (true){
if (temp.next==null){
return false;
}
if (temp.next.o==o){
temp.next.o=o2;
return true;
}
temp=temp.next;
}
}
//删除
public boolean delete(Type o){
temp=head.next;
while (true){
if (temp==null){
return false;
}
if (temp.o==o){
temp.pre.next=temp.next;
if (temp.next!=null){
temp.next.pre=temp.pre;
}
return true;
}
temp=temp.next;
}
}
//获得第index个节点
public MyNode getNode(int index){
if (head.next==null||!(getLength()>index)){
return null;
}
temp=head.next;
for (int i = 0; i < index; i++) {
temp=temp.next;
}
return temp;
}
//获得长度
public int getLength(){
int length=0;
temp=head;
while (temp.next != null) {
length++;
temp=temp.next;
}
return length;
}
//显示
public void showList() {
if (head.next == null) {
return;
}
temp = head.next;
while (true) {
System.out.println(temp);
temp = temp.next;
if (temp == null) {
break;
}
}
}
private class MyNode {
public Object o;
public MyNode(Object o) {
this.o = o;
}
public MyNode next;
public MyNode pre;
@Override
public String toString() {
return "MyNode{" +
"o=" + o +
'}';
}
}
}
栈的学习与字符型计算器
自定义栈
public class MyArrayStack<Type> {
private final int maxSize;
private final Object[] stack;
private int top=-1;
public MyArrayStack(int maxSize){
this.maxSize=maxSize;
stack=new Object[this.maxSize];
}
public boolean isFull(){
return top==maxSize-1;
}
public boolean isEmpty(){
return top==-1;
}
//查看顶部元素
public Type peekTop(){
@SuppressWarnings("unchecked")
Type o = (Type)stack[top];
return o ;
}
//进栈
public void push(Type value){
if (isFull()) {
throw new RuntimeException("栈满");
}
top++;
stack[top]=value;
}
//出栈
public Type pop(){
if (isEmpty()){
throw new RuntimeException("栈空");
}
//去除强转警告
@SuppressWarnings("unchecked")
Type value= (Type) stack[top];
top--;
return value;
}
public void showStack(){
if (isEmpty()){
return;
}
for (int i=top;i>=0;i--){
System.out.println(i+"=="+stack[i]);
}
}
}
计算器
public static void main(String[] args) {
MyArrayStack<Integer> numberStack=new MyArrayStack<Integer>(10);
MyArrayStack<Character> opStack=new MyArrayStack<Character>(10);
String expression="355+2+4*5/2+1";
String keepNumber = "";
int index=0; //
int num1=0;
int num2=0;
int op=0;
int res=0;
char ch=' ';
while (true){
ch=expression.substring(index,index+1).charAt(0);
//判断是否为符号
if (isOp(ch)){
//判断是否为空
if (!opStack.isEmpty()){
/**
* 思路:如果当前符号优先级小:就相等于把前面的计算了,如果大计算
*/
//判断符号优先级
if (priority(ch)<=priority(opStack.peekTop())){
num1=numberStack.pop();
num2=numberStack.pop();
op=opStack.pop();
res=cal(num1,num2,op);
numberStack.push(res);
opStack.push(ch);
}else {
opStack.push(ch);
}
}else {
opStack.push(ch);
}
}else {
//字符转数值-48等于对应的10进制数值
//numberStack.push(ch-48);
/**
* 用于解决多位数
*/
keepNumber+=ch;
if (index==expression.length()-1){
numberStack.push(Integer.valueOf(keepNumber));
}else if (isOp(expression.substring(index+1,index+2).charAt(0))){
numberStack.push(Integer.valueOf(keepNumber));
keepNumber="";
}
}
index++;
if (index>=expression.length()){
break;
}
}
/**
* 剩下的:从上到下符号优先级从大到小,所以直接取出计算
*/
while (true){
if (opStack.isEmpty()){
break;
}
num1=numberStack.pop();
num2=numberStack.pop();
op = opStack.pop();
res=cal(num1,num2,op);
numberStack.push(res);
}
System.out.println("结果="+numberStack.pop());
}
//*************************计算器功能拓展************************
//优先级
public static int priority(int op){
if(op=='*'||op=='/'){
return 1;
}else if (op=='+'||op=='-'){
return 0;
}else {
return -1;
}
}
//运算符
public static boolean isOp(char val){
return val=='*'||val=='/'||val=='+'||val=='-';
}
//计算方法
public static int cal(int num,int num2,int op){
int res=0;
switch (op){
case '+':
res=num+num2;
break;
case '-':
res=num2-num;
break;
case '*':
res=num*num2;
break;
case '/':
res=num2/num;
break;
default:
break;
}
return res;
}
}
前缀,中缀(正常),后缀表达式
中缀表达式 (3+4)5-2
前缀表达式 -+3452(从右向左进行入栈计算)
后缀表达式34+5*2-(从左向右进行入栈计算–推荐)
总的来说就是先排好符号的优先级,前缀没有后缀好用
中转后的思路
1.初始化一个栈s1,一个列队q2
2.从左到右扫描
3.遇到操作数,将其放入列队
4.遇到运算符,比较其与s1栈顶的运算符优先级:
如果s1为空,或为"(",则直接入栈
否则,运算符优先级比栈顶的高,也直接入栈s1
否则,将s1栈顶运算符放入q2中,再次回到如果重复判断
5.遇到括号时:
如果是左括号"(",直接入栈s1
如果十四右括号")",依次取出s1栈顶元素放入s2,直到遇到左括号
6.重复2-5,直到表达式的最右边
7.把s1中所有运算符放入q2
8.依次取出q2元素,结果为后缀表达式
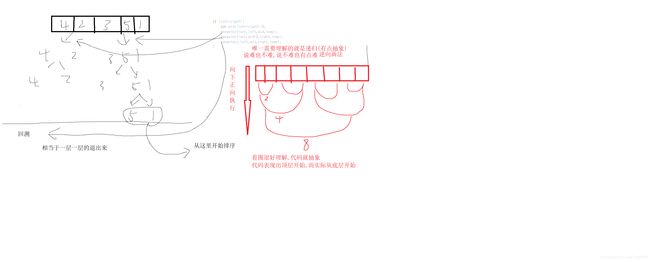
递归加八皇后问题解析
递归的理解
八皇后递归回溯解析
排序算法
冒泡排序
public static void main(String[] args) {
System.out.println(Arrays.toString(BubbleSortingOFMinToMax(new int[]{
1, 5, 4, -1})));
}
public static <T> T BubbleSortingOFMinToMax(T t){
if (t instanceof int[]) {
int[] arr=(int[]) t;
int temp=0; //用于交换
boolean isTransfer=false;//用于判断是否进行过交换,如果没有就结束了(证明摆好了)
/**
* 第一个for表示最多需要排序的次数,通过isTransfer来优化
*
* 第二个表示进行排序,通过i来优化次数每排一次后面就会减少一次
* -1是因为双指向(j+1)
*/
for (int i = 0; i < arr.length-1; i++) {
for (int j = 0; j < arr.length-1-i; j++) {
if (arr[j]>arr[j+1]){
isTransfer=true;
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
if (isTransfer){
isTransfer=false;
}else {
break;
}
}
return (T) arr;
}
return null;
}
选择排序
public static<T> T chooseSortingOFMinToMax(T t){
if (t instanceof int[]) {
int[] arr=(int[]) t;
int temp=0; //用于交换
int index=0;//用于记录当前交换者
/**
* 第一个for表示最多需要排序的次数,
*
* 第二个表示进行排序,通过i来优化次数每排一次后面就会减少一次
* +与后一个比较(忽略自己)
*/
for (int i = 0; i < arr.length-1; i++) {
temp=arr[i];
index=i;
for (int j = i+1; j < arr.length; j++) {
if (arr[j]<temp){
temp=arr[j];
index=j;
}
}
arr[index]=arr[i];
arr[i]=temp;
}
return (T) arr;
}
return null;
}
插入排序
public static<T> T insertSortingOFMinToMax(T t){
if (t instanceof int[]) {
int[] arr=(int[]) t;
for (int i = 0; i < arr.length-1; i++) {
int insertVal=arr[i+1];
int insertIndex=i;
while (insertIndex>=0&&insertVal<arr[insertIndex]){
arr[insertIndex+1]=arr[insertIndex];
insertIndex--;
}
arr[insertIndex+1]=insertVal;
}
return (T) arr;
}
return null;
}
希尔排序(优化版插入)
public static <T> T shellSortOfMinToMax2(T t){
if (t instanceof int[]) {
int[] arr=(int[]) t;
//分组排序
//收敛2分循环
for (int gap = arr.length/2; gap>0;gap/=2){
//组循环
for (int i = gap; i < arr.length; i++) {
int index=i;
int temp=arr[index];
//判断步长相等的对应元素大小()
if (arr[index]<arr[index-gap]){
/*
index-gap>=0用于判断是否越界(相当于排到最前面)
*/
while (index-gap>=0&&temp<arr[index-gap]){
arr[index]=arr[index-gap];
index-=gap;
}
arr[index]=temp;
}
}
}
return (T) arr;
}
return null;
}
快速排序(分组比较递归(边分边比较))(空间换时间)
public static <T> T quickSort(T t,int left,int right){
if (t instanceof int[]) {
int[] arr=(int[]) t;
int temp=0;
int l=left;
int r=right;
int pivot=arr[(l+r)/2];
while (l<r){
//找到最左边大于中间值得位置
while (arr[l]<pivot){
l++;
}
//找到最右边大于中间值得位置
while (arr[r]>pivot){
r--;
}
//相当于没有找到(分组完成)提前退出分组
if (l>=r){
break;
}
//交换
temp=arr[l];
arr[l]=arr[r];
arr[r]=temp;
if (arr[l]==pivot){
r--;
}
if (arr[r]==pivot){
l++;
}
}
if (l==r){
l+=1;
r-=1;
}
//向左递归
if (left<r){
quickSort(arr,left,r);
}
//向右递归
if (right>l){
quickSort(arr,l,right);
}
return (T) arr;
}
return null;
}
有点难啊
归并排序(递归分组比较(先分后比较))(空间换时间)
/**
*需要会递归回溯才能看得懂,懂就不难,不懂就呵呵呵
* @param arr
* @param left
* @param right
* @param temp
*/
public static void mergeSort(int[] arr,int left,int right,int[] temp){
if (left<right){
int mid=(left+right)/2;
//向左
mergeSort(arr,left,mid,temp);
//向右
mergeSort(arr,mid+1,right,temp);
//合并
merge(arr,left,mid,right,temp);
}
}
public static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i=left;
int j=mid+1;
int t=0;
//两边都有
while (i<=mid&&j<=right){
if (arr[i]<=arr[j]){
temp[t]=arr[i];
t++;
i++;
}else {
temp[t]=arr[j];
t++;
j++;
}
}
//左边有
while (i<mid){
temp[t]=arr[i];
t++;
i++;
}
//右边有
while (j<=right){
temp[t]=arr[j];
t++;
j++;
}
t=0;//回到0下标
int tempLeft=left; //arr当前组第一个位置
//temp数组值赋值给arr数组对应的位置段
while (tempLeft<=right){
arr[tempLeft]=temp[t];
t+=1;
tempLeft+=1;
}
}
查找算法
线性查找
public static int seqSearch(int[] arr,int value){
for (int i=0;i<arr.length;i++){
if (arr[i]==value){
return i;
}
}
return -1;
}
二分查找
public static int binarySearchOfMinToMax(int[] arr,int value,int left,int right){
if(left>right||value<arr[left]||value>arr[right]){
return -1;
}
int mid=(left+right)/2;
int midVal=arr[mid];
if (value>midVal){
return binarySearchOfMinToMax(arr, value, mid+1, right);
}else if (value<mid){
return binarySearchOfMinToMax(arr, value, left, mid-1);
}else {
return mid;
}
}
二分插值查找
public static int insertSearchOfMinToMax(int[] arr,int value,int left,int right){
if(left>right||value<arr[left]||value>arr[right]){
return -1;
}
//计算插值,插值只适用与线性数据
int mid=left +(right-left)*(value-arr[left])/(arr[right]-arr[left]);
int midVal=arr[mid];
if (value>midVal){
return insertSearchOfMinToMax(arr, value, mid+1, right);
}else if (value<mid){
return insertSearchOfMinToMax(arr, value, left, mid-1);
}else {
return mid;
}
}