【学习笔记】平衡树(1)

一、排序二叉树
排序二叉树的性质

1. 对于一个结点，若它的左子树不为空，那么它的左子树中所有结点的权值都小于这个结点的权值。
2. 对于一个结点，若它的右子树不为空，那么它的右子树中所有结点的权值都大于这个结点的权值。
   也就是说，排序二叉树的中序遍历就是它所有结点的权值排序后的结果。
   下图就是一棵排序二叉树。
   
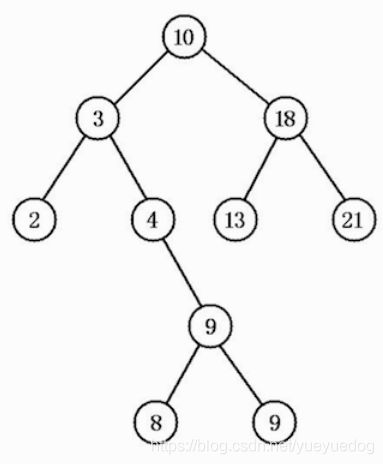
   排序二叉树的查找
   在排序二叉树中查找一个值x时，先从根结点开始考虑。
   如果根结点的权值等于x，那么直接返回根结点，若x小于根结点的权值，则递归处理左子树，反之递归处理右子树。
   如果需递归处理的左子树或右子树不存在，则说明排序二叉树中没有权为x的结点。
   在排序二叉树中查找第k个数（k小于等于排序二叉树的结点个数）时，先从根结点开始考虑。
   我们记录每个结点为根的子树的结点个数size。
   如果根结点的左儿子的size[l]大于等于k，那么递归处理左子树。如果k=size[l]+1，那么第 个结点就是根结点。否则将k减去size[l]+1，递归处理右子树。
   排序二叉树的插入
   将一个结点插入排序二叉树时，先从根结点开始考虑。
   对于一棵子树，如果它为空，则将待插入的结点置为它的根结点。否则，将待插入结点的权值与根结点的权值进行比较。
   若待插入结点的权值小于（等于）根结点的权值，则递归处理左子树，否则，递归处理右子树。
   排序二叉树的删除
   从排序二叉树中删除一个结点 A 分为两种情况。
   若结点 A 没有子结点或只有一个子结点，直接将它的子结点连到它的父亲结点，并删除结点 A 。若结点 A 有两个子结点，我们可以用它右子树中最小的结点取代它，并将它删除。查找排序二叉树的最小结点时，从根结点一直往左儿子走，直到走到某个没有左儿子的结点，这个结点就是这棵排序二叉树的最小结点。
   排序二叉树的实现

#include 
struct node {
     
    node* lc;
    node* rc;
    node* fa;
    int val, size;
} * root;
node* search(node* x, int val) {
     
    if (x == NULL)
        return NULL;
    else if (val == x->val)
        return x;
    else if (val < x->val)
        return search(x->lc, val);
    else
        return search(x->rc, val);
}
node* kth(node* x, int k) {
     
    if (x->lc != NULL) {
     
        if (k <= x->lc->size)
            return kth(x->lc, k);
        else
            k -= x->lc->size;
    }
    if (k == 1)
        return x;
    else
        k--;
    return kth(x->rc, k);
}
void insert(node* x, int val) {
     
    if (val <= x->val) {
     
        if (x->lc == NULL) {
     
            node* y = new node;
            y->val = val;
            y->fa = x;
            x->lc = y;
        } else
            insert(x->lc, val);
    } else {
     
        if (x->rc == NULL) {
     
            node* y = new node;
            y->val = val;
            y->fa = x;
            x->rc = y;
        } else
            insert(x->rc, val);
    }
}
void del(node* x) {
     
    if (x->lc == NULL) {
     
        if (x->rc == NULL) {
       // no child
            if (x->fa != NULL) {
     
                if (x == x->fa->lc)
                    x->fa->lc = NULL;
                else
                    x->fa->rc = NULL;
            }
        } else {
       // only right child
            x->rc->fa = x->fa;
            if (x->fa != NULL) {
     
                if (x == x->fa->lc)
                    x->fa->lc = x->rc;
                else
                    x->fa->rc = x->rc;
            }
        }
    } else {
     
        if (x->rc == NULL) {
       // only left child
            x->lc->fa = x->fa;
            if (x->fa != NULL) {
     
                if (x == x->fa->lc)
                    x->fa->lc = x->lc;
                else
                    x->fa->rc = x->lc;
            }
        } else {
       // both child
            node* y = kth(x->rc, 1);
            x->val = y->val;
            y->rc->fa = y->fa;
            if (y == y->fa->lc)
                y->fa->lc = y->rc;
            else
                y->fa->rc = y->rc;
            x = y;
        }
    }
    while (x != NULL) {
       // update size
        x->size--;
        x = x->fa;
    }
}

平衡树和Treap
我们知道，排序二叉树的复杂度是O(n log n)的，除非我们遇到了极端数据。
例如，我们通过特定的插入顺序，把二叉搜索树变成一整条链，这时候我们每次操作的复杂度就很不幸变成了O(n)的。
所以我们要用平衡树来维护，它的特点在于如果它不平衡的时候就会自己旋转，
然后想办法让这个树趋于平衡。
我们只要保证它的深度是O(log n)级别的，那么每个操作的复杂度也就有了保障。
下面我们来介绍一下 Treap。
什么叫 Treap？Treap = Tree + Heap 。
我们发现，二叉搜索树的复杂度爆炸的原因是被针对了，那么我们给每个结点一个权值，让这个权值组成一个堆，在此基础上我们维护的二叉平衡树就不再是与输入顺序有关，而是与我们给的权值有关。
具体来说，每个结点都在存储数值的同时，另外存储了一个值，这个值叫做每个结点的 权值，每个结点的权值一定大于等于（或小于等于，取决于你自己的实现方式）它的两个孩子。
下图是一个大根堆的 Treap，左边是数值，右边是权值。

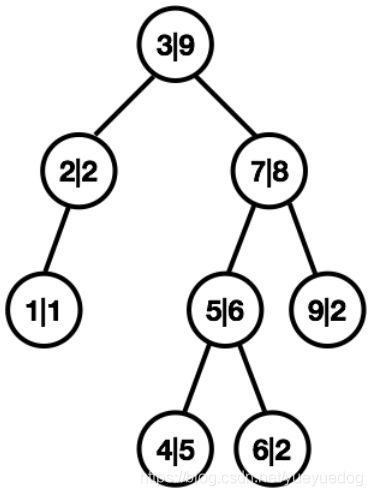
那么我们该如何维护一个同时满足二叉搜索树和堆性质的东西呢？
我们先假设当前的 Treap 是合法的（显然空树是合法的），我们只要保证在插入和删除结点的时候，它依旧合法，那么它就是合法的。
首先我们引入一个基础操作：旋转

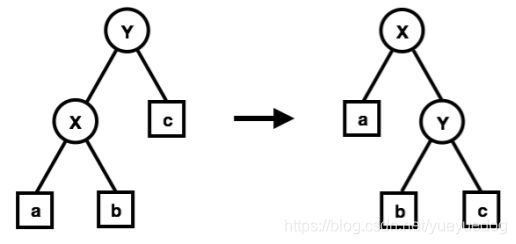
其中， a,b,c三个是子树（可以为空），X,Y 是结点。
在旋转的时候，我们可以保持住这个二叉搜索树的性质。我们通过这个操作可以维护堆的性质而不破坏二叉搜索树的性质。
如何实现插入？
有了旋转操作就很简单了，我们首先插入一个结点，按照二叉搜索树的方式插
入，在插入完成以后我们可能发现它现在不满足堆的性质。
那么我们开始将这个结点旋转，直到它满足堆的性质。
这一个操作与“堆的插入”操作非常的相似。不同之处在于堆的插入是直接交换，而我们需要旋转。
如何实现删除？
如果按照二叉搜索树的方式也是可以的，不过较为麻烦。这里介绍一个稍微简单点的方式。
我们可以将要删除的结点旋转到叶子然后删除。
对于一个结点，比较它的左右儿子，哪个权值较大就换到哪里去（注意判断有儿子为空的情况，这时候就要换到另一个儿子上），直到到达一个叶子结点，然后我们将它父亲指向它的指针改为空即可。
举个栗子

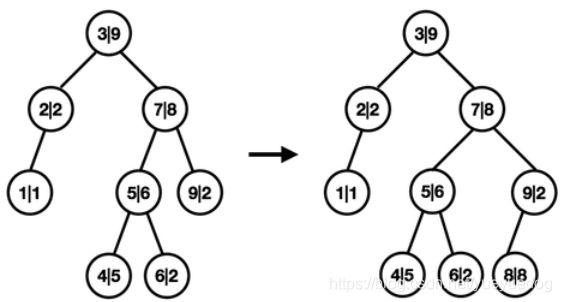
我们决定插入一个结点，数值为8 ，权值我们随机到了8 。（实际上建议权值随机范围大一点，这里因为写不下所以权值均为10以内）
我们比较后，发现它应当是插入在9的左孩子。
之后我们就要开始旋转了。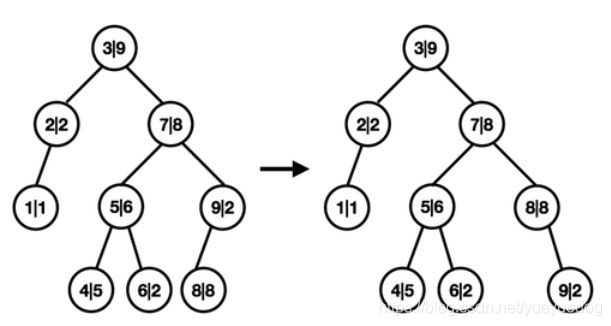
求前驱/后继
以前驱为例，后继是相似的求法。
我们首先访问根。
如果根的数值比x小，那么就访问根的右子树，并递归下去。
如果根的数值比x大或相等，那么就访问根的左子树，并递归下去。
如果我们发现我们访问到了 空结点 ，那么我们就返回一个 无解 。
一旦我们在某个结点向 右子树 递归并且发现右子树是 无解 的，那么就返回这个结点本身。
否则我们就返回当前得到的解。
注意：如果我们访问了某个结点的左子树并得到无解，那么说明在整个子树内是无解的。
我们最终访问的点数仅与深度有关，所以复杂度是O(log n)的。
求第 k 小
我们需要在 Treap 的结点中维护它的子树大小，并且需要在旋转的时候正确维护子树大小。
我们首先访问根。
如果根的左子树的大小==k-1，那么我们可以直接返回根的值。
如果根的左子树的大小 j-size[l]-1小即可。（ 表示左子树的大小）
如果根的左子树的大小>k-1，那么就直接递归到左子树。
最多访问的点数也仅仅与深度有关，所以复杂度是O(log n)的。
求第k大与第k小是相似的，甚至你可以直接将第k大改为第k小来求。
求 rank（比 x 小的数有几个）
我们需要在 Treap 的结点中维护它的子树大小，并且需要在旋转的时候正确维护子树大小。
我们首先访问根。
如果根的值比x小，那么根和左子树都比size[l]+1小，所以就返回 再加上右
子树递归下去得到的值。（size[l]表示左子树的大小）
如果根比x大或者相等，那么直接递归左子树就行。
其他操作（略）
求第 1 ~ k 小的和
我们需要在 Treap 的结点中维护它的子树大小和子树和，并且在旋转的时候正确维护它们。
与求第k大的情况相似。
修改单点的数值
先删除这个点，再插入回来。
可以考虑重复利用这个指针。
查询一个数是否存在
与求rank相似。
Treap的实现

#include 
#include 
using namespace std;
struct node {
     
    int size;
    int weight;
    int val;
    node *ch[2];
};
node *root;
node *null;
node *new_node(int x) {
     
    static node a[100005];
    static int top = 0;
    node *t = &a[top++];
    t->size = 1;
    t->weight = rand();
    t->val = x;
    t->ch[0] = null;
    t->ch[1] = null;
    return t;
}
void rotate(node *&x, int c) {
     
    node *y = x->ch[c];
    x->ch[c] = y->ch[!c];
    y->ch[!c] = x;
    y->size = x->size;
    x->size = x->ch[0]->size + x->ch[1]->size + 1;
    x = y;
}
void insert_node(node *&x, node *y) {
     
    if (x == null) {
     
        x = y;
        return;
    }
    x->size++;
    int c;
    if (y->val > x->val) {
     
        c = 1;
    } else {
     
        c = 0;
    }
    insert_node(x->ch[c], y);
    if (x->ch[c]->weight > x->weight) {
     
        rotate(x, c);
    }
}
void delete_node(node * &x, int k) {
     
    if (x == null) {
     
        return;
    }
    x->size--;
    if (x->val == k) {
     
        int c;
        if (x->ch[0]->weight > x->ch[1]->weight) {
     
            c = 0;
        } else {
     
            c = 1;
        }
        rotate(x, c);
        delete_node(x->ch[!c], k);
    } else {
     
        int c;
        if (x->val > k) c = 0;
        else c = 1;
        delete_node(x->ch[c], k);
    }
}
int find_maxxer_node_val(node *&now, int k) {
     
    // 不可以相等
    if (now == null) return 999999999;  // inf
    if (now->val > k) {
     
        return min(now->val, find_maxxer_node_val(now->ch[0], k));
    } else {
     
        return find_maxxer_node_val(now->ch[1], k);
    }
}
int find_minner_node_val(node *&now, int k) {
     
    // 可以相等
    if (now == null) return -999999999;  // -inf
    if (now->val <= k) {
     
        return max(now->val, find_minner_node_val(now->ch[1], k));
    } else {
     
        return find_minner_node_val(now->ch[0], k);
    }
}
bool find(node * &now,int k) {
     
    if (now == null) {
     
        return false;
    }
    if (now->val == k) {
     
        return true;
    } else if (now->val < k) {
     
        return find(now->ch[1], k);
    } else {
     
        return find(now->ch[0], k);
    }
}
int get_kth(node *&now, int k) {
     
    if (k == now->ch[0]->size + 1) {
     
        return now->val;
    } else if (k <= now->ch[0]->size) {
     
        return get_kth(now->ch[0], k);
    } else {
     
        return get_kth(now->ch[1], k - now->ch[0]->size - 1);
    }
}
int get_rank(node *now, int k) {
     
    if (now == null) return 1;
    if (now->val < k) {
     
        return now->ch[0]->size + 1 + get_rank(now->ch[1], k);
    }
    return get_rank(now->ch[0], k);
}
int main() {
     
    null = new_node(0);
    null->ch[0] = null;
    null->ch[1] = null;
    null->size = 0;
    null->weight =- 1;
    return 0;
}