python 一维数组所有元素是否大于_Python数据分析第二节 NumPy进阶

上一节我们学习了一维数组生成和计算，这一节将引入多维数组。难度会有所加大，请大家认真阅读，下载安装好Anaconda进行python练习～

第二节 NumPy进阶

目录

一. 多维数组

二. 二维数组的加减乘除

三. 二维数组的通用方法

四. 二维数组的索引和分片

五. 实用方法

➡ 一. 多维数组

多维数组的学习可以联想多维坐标系，比如一维、二维、三维坐标。下面的图很形象的反映的多维数组的样子

创建一组二维数组，如下

# 二维数组

import numpy as npnested_list = [[1, 2], [3, 4]]data = np.array(nested_list)print(data)

# 输出的结果如下：[[1 2]
 [3 4]]

可以看到，二维数组也是用空格分隔的，并且分成了两行。列表中的第一个元素 [1, 2] 在第一行，第二个元素 [3, 4] 在第二行。

那么问题来的：还记得上一节学过的ones()和zeros()方法吗？(忘记的话要记得复习哟)怎么用这两个方法创建二维数组呢？

与之前的区别在于，创建二维数组要传入一个包含行和列信息的元组。比如：np.ones((m, n)) 表示创建一个 m 行 n 列且元素全为 1 的二维数组；np.zeros((m,n))表示创建一个m行n列且元素全为0的二维数组。

ones = np.ones((3, 2))print(ones)

输出的结果就为：

[[1. 1.]
 [1. 1.]
  [1. 1.]]

接下来我们来认识几个描述多维数组的属性：

⚫ ndim：多维数组维度的个数。例如：二维数组的 ndim 为 2；

⚫ shape：多维数组的形状。它是一个元组，每个元素分别表示每个维度中        数组的长度。对于 m 行和 n 列的的数组，它的 shape 将是 (m, n)。因此，shape 元组的长度(元素个数)就是 ndim 的值；

⚫ size：多维数组中所有元素的个数。shape 元组中每个元素的乘积就是 size 的值；

⚫ dtype：多维数组中元素的类型。

import numpy as npdata = np.array([[1, 2, 3], [4, 5, 6]])print('ndim:', data.ndim)print('shape:', data.shape)print('size:', data.size)print('dtype:', data.dtype)

输出的结果为：

ndim: 2
shape: (2, 3)
size: 6
dtype: int64

注意：int64 是 numpy 提供的类型，表示 64 位的整数

还需要强调的是，对于 [1 2 3] 这样的一维数组，它的 shape 是 (3,)，表示有三个元素，且后面的逗号是不能省略的，否则会被认为是加了括号的 3。

➡ 二. 二维数组的加减乘除

维数组间的加减乘除和一维数组间的并无大致，也是对应位置的元素进行计算。这里不再赘述，我们直接来看图解：

减法、乘法和除法也都是如此。二维数组和数学中的 矩阵 很相似，常被用于进行矩阵间的运算。但二维数组间直接用 * 进行计算的方式和矩阵乘法计算的方式并不相同，应该用 @ 符号进行矩阵间的乘法计算。

维度一样的数组可以进行计算的条件是形状shape一样，也就是说m行n列的数组需要和m行n列的数组进行计算。否则将会报错。

如果二维数组和一维数组进行加减乘除运算，会不会报错呢？

答案是不会报错！

这里需要介绍一下numpy中的广播规则，当运算中的 2 个数组的形状不同时，numpy 将自动触发广播机制，它具体的规则是：在较小维度数组的 shape 元组前补 1，直到两个数组的 shape元组长度相同。接着将元素在值为 1 的维度上进行复制，直到两个数组的形状相同。

如下图所示，一维数组[1 1]会自动变成每一行都是[1 1]再进行计算！

这种触发广播机制进行计算的前提还要有相同的列数。即shape(m,n)的n要相同。

import numpy as npdata = np.array([[1, 2, 3], [4, 5, 6]])ones = np.ones(3)print(data + ones)

输出结果为：

[[2. 3. 4.]

 [5. 6. 7.]]

➡ 三. 二维数组的通用方法

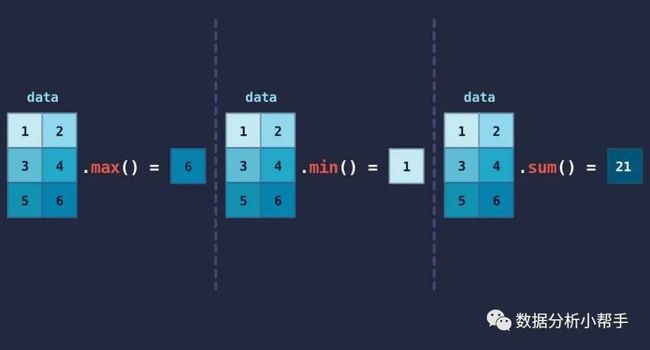
二维数组的通用方法和一维数组的通用方法的基本用法类似，只是多了一个维度的数据而已。这里不再细说，看个图解你就明白了。

上面讲的是对整个维度所有数值进行的操作。当然也可以对某一个维度进行相应的计算，比如找出每一行的最大值或者每一列的最大值。想要达到这个目的，还需要再引入一个概念---轴(axis).

在 numpy 中，我们可以用 axis 参数来指定轴，从 0 开始依次增加递增的数分别对应着不同的轴。

在一维数组中，axis=0 就代表着它唯一的轴；二维数组中 axis=0 和 axis=1 代表其中的行轴和列轴；在三维数组中，axis=0、axis=1 和 axis=2 分别代表对应的三条轴。下图清晰的展示了 axis 和对应轴的关系：

在一维数组中因为只有一个轴，一般用不到 axis。需要注意的是，在二维数组中 axis=0 的轴是向下的，和一维数组中有所不同，千万不要混淆。

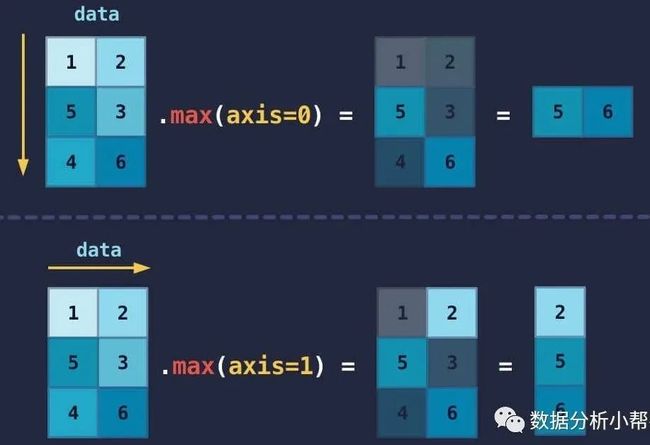
在通用方法中，通过 axis 参数可以指定计算方向。以二维数组中的 max() 方法为例，指定 axis=0 将会在行轴方向求最大值，指定 axis=1 将会在列轴方向求最大值。

import numpy as npdata = np.array([[1, 2], [5, 3], [4, 6]])# 不指定 axisprint(data.max())# 输出：6#指定 axis# axis=0print(data.max(axis=0))# 输出：[5 6]# axis=1print(data.max(axis=1))# 输出：[2 5 6]

看代码可能比较抽象，我们用图示来展示一下：

对于其他通用方法，axis 的作用是一样的。希望大家在理解后能够举一反三，这里就不再举更多的例子了。

➡ 四. 二维数组的索引和分片

二维数组的索引和分片同样和一维数组类似，只是在行索引的基础上再加上列索引。形如 data[m, n]，其中 data 是二维数组，m 是行索引或分片，n 是列索引或分片。

那么，data[0, 1] 就表示获取 data 中第一行第二列的元素。如果省略第二个参数 n 的话表示获取所有列，data[0] 就表示获取整个第一行，相当于 data[0, :]。

如果想要获取第一列则可以写成 data[:,0]；如果想获取 2、3 两行可以写成 data[1:3]，相当于 data[1:3, :]。你可以将索引和分片结合起来，以获取二维数组中你想要的任意数据。

下面看一个代码举例：

import numpy as npdata = np.array([[1, 2], [3, 4], [5, 6]])print(data)# 输出：[[1 2] [3 4] [5 6]]# 输出第一行第二列的数字print(data[0, 1])# 输出：2# 输出第一列组成的数组print(data[:, 0])# 输出：[1 3 5]# 输出第二到三行数组print(data[1:3])# 输出：# [[3 4]#  [5 6]]

是不是感觉索引和分片变得有些抽象了呢，不要着急，多体会体会就能记住了，加油

➡ 五. 实用方法

1. arange()方法

arange()是可以直接生成数组的，不再需要array()来生成

我们直接看几个例子：

import numpy as np# 生成 1-9 的数组print(np.arange(1, 10))# 输出：[1 2 3 4 5 6 7 8 9]# 生成 0-9 的数组print(np.arange(10))# 输出：[0 1 2 3 4 5 6 7 8 9]# 生成 1-9 的数组，步长为 2print(np.arange(1, 10, 2))# 输出：[1 3 5 7 9]

总结：

生成m到n的数组就用arange(m, n+1)

生成0到n的数组就用arange(n+1)

生成m到n的数组且步长为z的数组就用arange(m, n+1, z)

2. 随机方法

Python 中有 random 模块来生成随机数，numpy 针对多维数组也集成了 random 模块，并且更加方便好用。

这里只介绍其中的 rand() 方法和 randint() 方法，更多方法大家可以在需要时查询使用。

numpy 中的 np.random.rand() 方法和 Python 中 random.random() 方法类似，都是生成 [0, 1) 之间的随机小数。不同的是，numpy 中的 np.random.rand() 方法可以生成多个 [0, 1) 之间的随机小数，只需我们传入要生成的随机数组的形状(shape)即可。

来看一下相应代码：

import numpy as np# 不传参数时print(np.random.rand())# 输出：0.1392571183916036# 传入一个参数时(传入shape为(3，)print(np.random.rand(3))# 输出：[0.7987698  0.52115291 0.70452156]# 传入多个参数时(传入shape为2行3列)print(np.random.rand(2, 3))# 输出：# [[0.08539006 0.97878203 0.23976172]#  [0.34301963 0.48388704 0.63304024]]

同理，numpy 中的 np.random.randint() 方法和 Python 中的 random.randint() 类似，不同之处在于，random.randint(m, n) 生成的是 [m, n] 之间的整数，而 np.random.randint(m, n) 生成的是 [m, n) 之间的整数，这点一定注意要区分。

除此之外，np.random.randint() 方法第三个参数支持传入生成的数组的形状，例子如下：

import numpy as np# 不传入形状时print(np.random.randint(0, 5))# 输出：3# 形状为一维数组时(shape为(3，))print(np.random.randint(0, 5, 3))# 输出：[4 0 1]# 形状为二维数组时(shape为(2，3))print(np.random.randint(0, 5, (2, 3)))# 输出：# [[0 2 1]#  [4 2 0]]

这就是第二节多维数组的全部内容大家可以下载好Anaconda进行代码的相应练习，熟能生巧，实操才能快速掌握理论

?

长按关注公众号

欢迎留言交流