决策树算法模型的归类与整理(ID3&C4.5&CART&线性二分类&非线性二分类)
决策树算法模型的归类与整理(ID3&C4.5&CART&线性二分类&非线性二分类)
一、 总结摘要
决策树模型在监督学习中非常常见,可用于分类(二分类、多分类)和回归。虽然将多棵弱决策树的Bagging、Random Forest、Boosting等tree ensembel 模型更为常见,但是“完全生长”决策树因为其简单直观,具有很强的解释性,也有广泛的应用,而且决策树是tree ensemble 的基础。一般而言一棵“完全生长”的决策树包含,特征选择、决策树构建、剪枝(包括预剪枝和后剪枝)三个过程,接下来我将简要地梳理并比较ID3、C4.5、CART这3个算法。
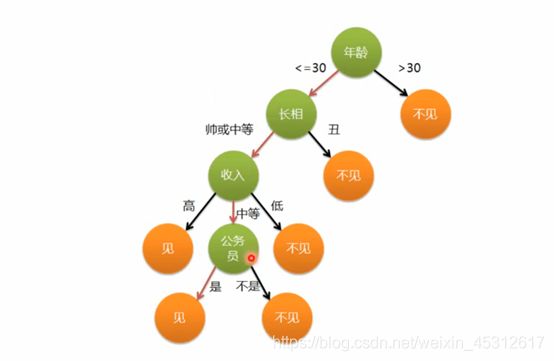
例如上图即为一棵简单的决策树模型,可以用来简单判定并预测一位女孩是否要去见她的相亲对象,这个过程与评判标准即可用上面的决策树模型来加以辅助判定。
决策树的优点与缺点
优点:
- 决策树算法中简单的决策规则建立决策树模型的过程非常容易理解;
- 决策树模型可以可视化,非常直观;
- 应用范围广,可用于分类和回归,而且非常容易做多类别的分类;
- 能够处理数值型和连续的样本特征。它比较适合分析离散型数据,若数据为连续型,则要先转换成离散的数据再进行分析。
缺点: - 很容易在训练数据中生成复杂的树结构,造成过拟合情况(overfitting)。剪枝可以缓解过拟合带来的的负作用,常用方法是限制树的高度、叶子节点中的最少样本数量;
- 学习一棵最优的决策树被认为是NP-Complete问题。实际中的决策树是基于启发式的贪心算法建立的,但这种算法不能保证建立全局最优的决策树。Random Forest 引入随机能缓解这个问题。
时间复杂度与空间复杂度分析
时间复杂度O(NMD):O(NMD), N是sample的大小,M是feature的数量,D是树的深度。cart生长时,把所有feature内的值都作为分裂候选,并为其计算一个评价指标(信息增益、增益比率、gini系数等),所以每层是O(NM),D层的树就是O(NM*D)。
空间复杂度o(N + M * Split * TreeNum ):N为样本数量,M为特征数量,Split为平均每个特征的切分点数量,TreeNum为如果为随机森林,随机森林的数目数量。
70年代后期至80年代,Quinlan开发了ID3算法,后来,他将ID3算法进行改进,得到了C4.5算法,到1984年,由多位统计学家共同研究,又得出了CART算法。因此,ID3到C4.5再到CART算法,都是建立在决策树模型的基础之上的迭代和更新,通过算法内部的调整不断对决策模型进行优化和改进。接下来,我将详细介绍并比较这三种算法的用途及原理。
二、 ID3算法
ID3由Ross Quinlan在1986年提出。ID3决策树可以有多个分支,但是不能处理特征值为连续的情况。决策树是一种贪心算法,每次选取的分割数据的特征都是当前的最佳选择,并不关心是否达到最优。在ID3中,每次根据“最大信息熵增益”选取当前最佳的特征来分割数据,并按照该特征的所有取值来切分,也就是说如果一个特征有4种取值,数据将被切分4份,一旦按某特征切分后,该特征在之后的算法执行中,将不再起作用,所以有观点认为这种切分方式过于迅速。
ID3算法十分简单,核心是根据“最大信息熵增益”原则选择划分当前数据集的最好特征,信息熵是信息论里面的概念,是信息的度量方式,不确定度越大或者说越混乱,熵就越大。在建立决策树的过程中,根据特征属性划分数据,使得原本“混乱”的数据的熵(混乱度)减少,按照不同特征划分数据熵减少的程度会不一样。在ID3中选择熵减少程度最大的特征来划分数据,也就是“最大信息熵增益”原则。
由于决策树会根据最大信息增益来对结点进行划分,因此信息增益的计算尤为重要,公式如下:
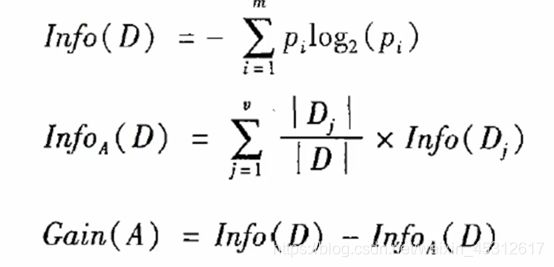
注明:p(i)为某种情况出现的概率值,Info(D)为整体的信息熵,InfoA(D)表示在选取属性A作为节点对整体进行划分后信息熵值,Gain(A)为属性A的信息增益大小。
接下来我们通过具体实例来说明ID3算法的运行过程
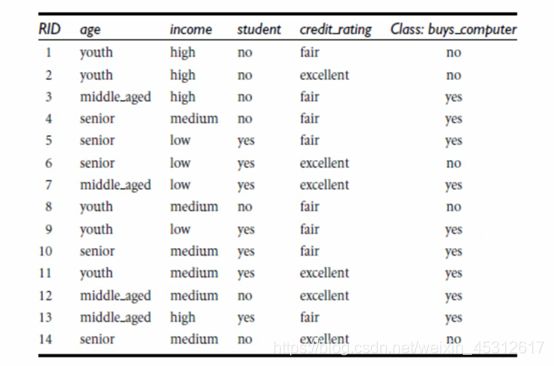
图中表示的数据为年龄,收入,是否为学生与信用等级对买电脑这个动作的决策和影响,及通过表中的4个不同属性对最终的行为进行判断和预测,我们用ID3算法来进行描述。
根据我的观察可以大致画出的决策树模型如下,等下可以与python所画出的进行比较,观察人为构建与机器建模的差异何在。
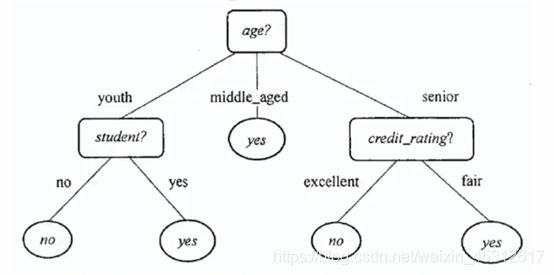
选择age作为根节点后可以继续向下画图,得出图如下

到此处可见,该模型的决策树已经大体成型,接下来通过python代码来做机器建模,绘制决策树。
编程环境我选择了Anaconda中的jupyter Notebook编译器作为运行平台,好处是jupyter是一个在线编辑器,并且可以利用Anaconda中内置的多种数据包,包括了决策树所需要的numpy、math、pandas等等,后续的C4.5和CART算法均使用此平台环境,后面将不再赘述。
代码执行情况如下:
首先将上述表格的内容整理到excel中,标记好各个属性和结果,以便后续的代码调用。
开始建立树模型并通过CSV包来读取数据内容
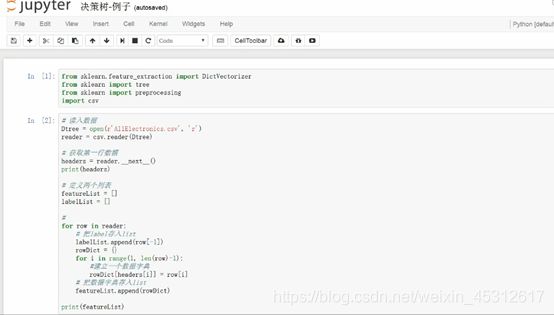
读入数据后建立字典来存储数据内容,根据属性来建立键值对,一一对应,将此部分运行即可得到图中下方的一条条字典数据。

字典数据如下

将上述的字符数据转换为1和0的表示,方便计算机的运算,转换后的结果如下图所示
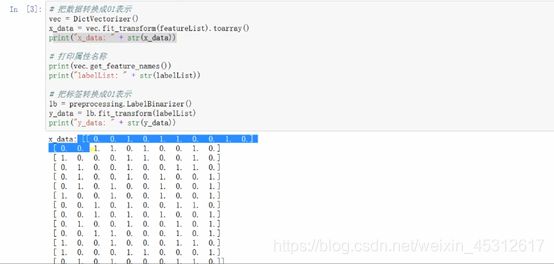
可以将excel中的数据与上述1、0矩阵进行比较,确实是一一对应的关系,1和0都代表了不同属性下面的不同状态

准备工作完成后,开始创建决策树模型并导出测试
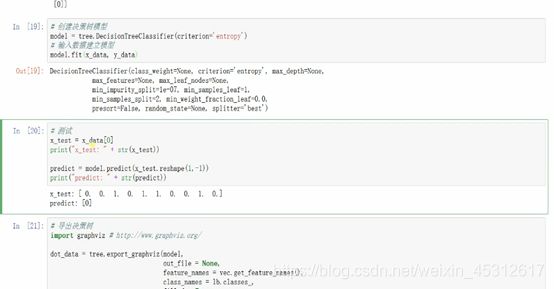
测试结果如下,此处还没有将决策树图形化展现出来,而是得出了数字化的结果,下面我会将图形化的一同展现。

最后一步,导出决策树,通过graphviz将决策树模型具象化导出,同时保存为PDF格式的图片,方便后续的使用和研究。
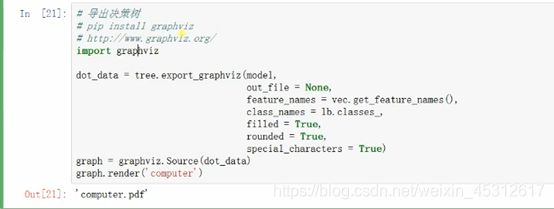
最终决策树如下
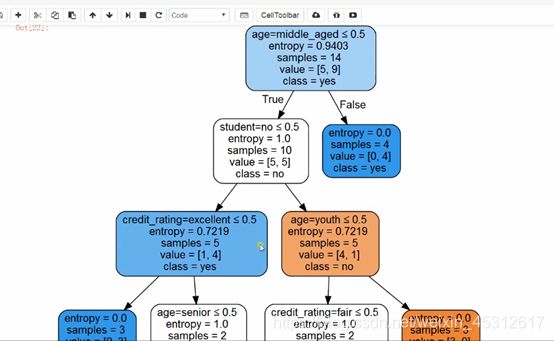
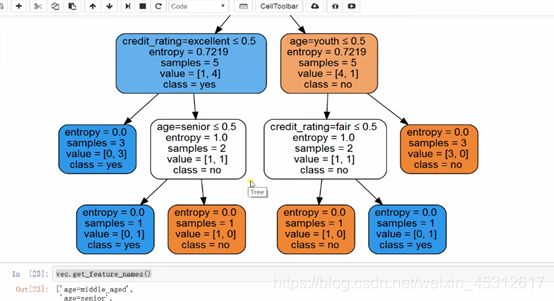
由此图可见,python所绘制的决策树与我上图中人为手绘的有所差别
python所建立的决策树模型中左边的子树都是True,而右边的子树都是False,而且整棵树是一个只有二分支的二叉树,并非是有多个分支的决策树;
其次,最终图并没有按照先前分析的,选取最大增益的属性进行节点的划分,因此树模型的整体结构看起来较为复杂,树的深度和复杂度有所增加。但是最终的分析结果完全无误,且运算过程遵循最大增益的判定规则。
经过分析,原因可能是ID3算法的提出距今已经有几十年的时间,中间必定经历过数次的更新和迭代,在不断优化和探索中,因此python所绘制的ID3模型图与人为构想的有些许差别,但是本质还是一样的。
三、 C4.5算法
C4.5是Ross Quinlan在1993年在ID3的基础上改进而提出的。ID3采用的信息增益度量存在一个缺点,信息增益的方法倾向于首先选择因子数较多的变量,因为属性值多的Feature会有相对较大的信息增益(信息增益反映的给定一个条件以后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大)。
为了避免这个不足,C4.5中将信息增益作为节点划分的标准摒弃,改为使用信息增益率(gain ratio)来作为选择分支的准则。信息增益率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的Feature。除此之外,C4.5还弥补了ID3中不能处理特征属性值连续的问题。但是,对连续属性值需要扫描排序,会使C4.5性能下降。
具体的算法公式如下:信息增益率的计算也是建立在信息增益的基础上改进和使用的,C4.5算法即是将ID3算法中选择特征的标准用信息增益比代替。
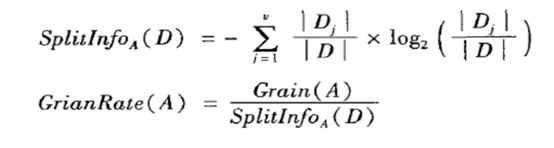
具体的实例在此不再描述,改进后的C4.5在准确率方面有所提高,同时在ID3算法的基础之上有4项改进:
第一就是用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多的属性的不足;
第二就是在树构造过程中进行剪枝,有效抵抗了决策树模型中过拟合问题带来的准确率低下的问题;
第三就是能处理非离散的数据,减少了将连续数据转换成离散数据处理的步骤,提高了算法效率;
第四就是能处理不完整的数据。
四、 CART算法
经过迭代和演化,决策树模型已经从ID3改进到C4.5,后来,经过统计学家的共同研究,又提出了CART算法。
CART(Classification and Regression tree)分类回归树算法是由L.Breiman,J.Friedman,R.Olshen和C.Stone于1984年提出。ID3中根据属性值分割数据,之后该特征不会再起作用,这种快速切割的方式会影响算法的准确率。而CART是一棵二叉树,采用二元切分法,每次把数据切成两份,分别进入左子树、右子树。而且每个非叶子节点都有两个孩子,所以CART的叶子节点比非叶子多1。
相比ID3和C4.5,CART应用要多一些,既可以用于分类也可以用于回归。CART分类时,使用基尼指数(Gini)来选择最好的数据分割的特征,gini描述的是纯度,与信息熵的含义相似。CART中每一次迭代都会降低GINI系数。下图显示信息熵增益的一半,Gini指数,分类误差率三种评价指标非常接近。回归时使用均方差作为loss function。基尼系数的计算与信息熵增益的方式非常类似,公式如下:

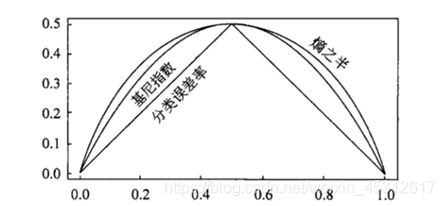
由此可知,CART决策树的生成就是递归的构建二叉决策树的过程,同时使用基尼系数最小化准则来进行特征选择,生成二叉树。
下面通过实例(通过人的不同属性值来判定是否会拖欠贷款)来具体研究CART算法在时间中的应用。
表格数据如下图所示:
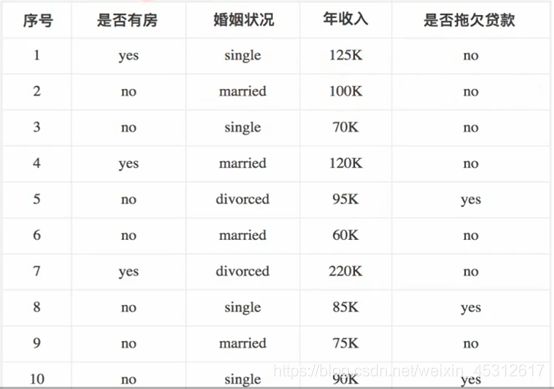
首先要根据表格数据,分别计算不同属性它们的Gini系数增益,取Gini系数增益最大的属性来作为决策树的根节点属性。
若根据是否有房来进行划分时,基尼指数的增益计算过程如下,二叉树的左节点表示Yes,右节点表示No。
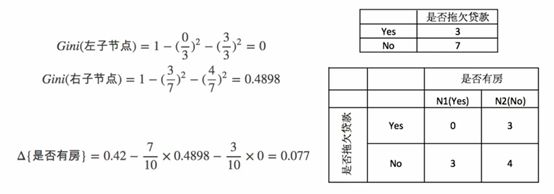
按照此方法即可依次计算其他各个属性的Gini系数

由此比较可得,婚姻状况与是否有房的Gini系数大小相同,故根节点采用这两种属性值来进行划分均可,对后续无影响。根据年收入来划分时,由于年收入的数字是连续型变量,因此在计算Gini系数时需要将其转化为离散型变量来计算,过程如下:
将列表中相邻两个的年收入的平均值都计算出来,在依次以各个平均数作为划分标准来进行Gini系数的计算,选择其中最大的值所对应的年收入平均值来作为高低收入的分界限,这样即解决了连续变量与离散变量的转换问题。

由图可知,将80和110作为高低收入的分界点是可行的。
选出根节点并按照该顺序递归推导,最终得出的CART如下图:
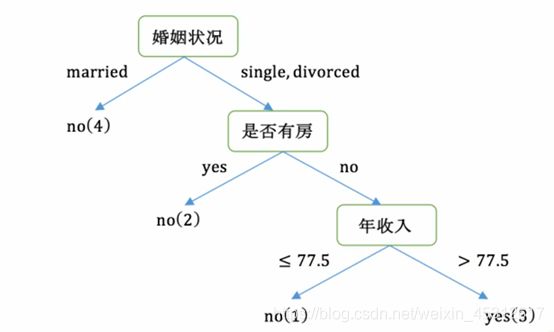
python构建CART的过程与上述ID3类似,在此不再进行赘述,jupyter notebook中的部分过程如截图所示:

最终绘制的CART如下:


为了削减过拟合问题给最终的预测结果带来的影响,我们可以对二叉树进行剪枝的操作,剪枝分为两种,分别是预剪枝和后剪枝,顾名思义,区别在于剪枝先后顺序的不同。具体情况如下:
下面为两棵二叉树

预剪枝:根据日常经验在众多属性值当中人为的去掉一些不太重要的属性,即在建立决策树之前去掉一些属性;
例如在某项列表中共有20个属性,在编程建模之前通过观察,可以人为去掉10个不重要的属性,只用剩下10个来进行判断。
后剪枝:在建立决策树之后根据二叉树的数据观察,去掉一部分支树;
例如在上左图中,经过A3的共100个数据,其中90个为No,10个为Yes,故A5里有10个数据,再经过判断,选择Yes的有9个,No的有1个,综上计算,经过A3后,99个数据为类B,只有1个为类A,因此我们对其进行后剪枝得到了右图。
去掉的部分只有1个A类,属于少数的特殊情况,实际上可能是由于过拟合造成的,也可以视为噪音或者干扰所造成的。
以上即为决策树中剪枝操作的叙述和举例,在实际应用中,剪枝操作可以抵抗过拟合的情况,同时可以降低决策树的复杂度。
五、 线性二分类与非线性二分类
在决策树的实际应用中,可以进行预测和分类,因此二叉树也分为回归树和分类树,出上述三种算法外,决策树还可以用于做线性二分类与非线性二分类。
下面将会通过点阵划分来具体分析这两种方法,编程环境依旧为Anaconda中的Jupyter Notebook编译器。
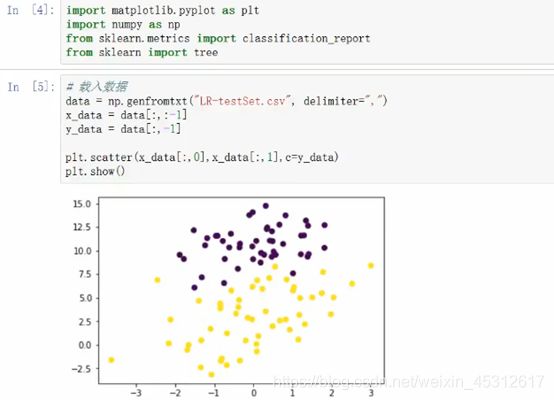
点阵的划分实际上也需要用到决策树的判定过程,我们将随机点阵进行坐标化,给了每个点一个确切的定位,之后即可设定判定规则,根据坐标X和Y值的范围来将不同颜色的点集划分出来。结果如图:


同样为很复杂的决策树,需要再次将其图形化即可得到最终的划分点集

最终结果如下图:

上述过程中通过修改其中的部分参数值,比如决策树的深度或者节点所需的最小样本数等等参数会得到不同的划分边界,同时划分的精准度也会有所不同,如果想要得到良好的划分结果往往需要不断的调整参数值,这里存在一个试的过程。
非线性二分类的简要演示
具体代码部分与上述类似,在此我们不再赘述
以下为非线性二分类的点阵图:
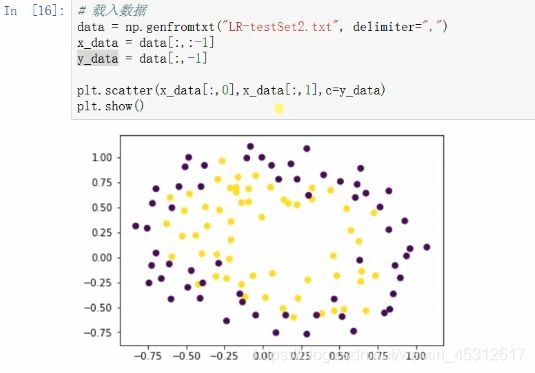
同理,我们需要将决策树转化为可视化的图片,具体操作过程与二分类中大同小异,代码截图见下方:
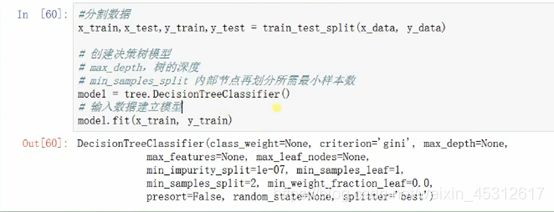
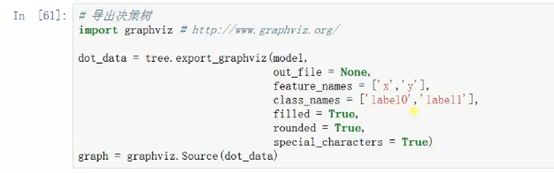

导出最终决策树的划分模型如下图:

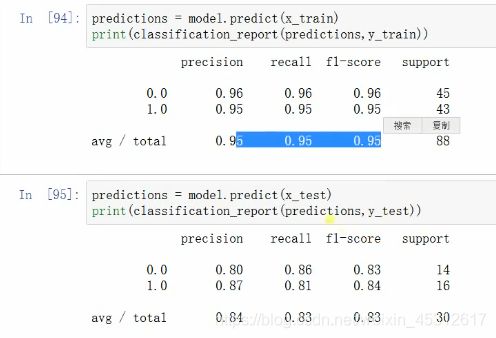
根据上下两张图划分的对比,我们可以粗略看出,在对非线性二分类的划分中,由于边界情况较为复杂,划分的效果不如线性划分的结果好,运行刚才的代码,我们可以看出数字化的结果。
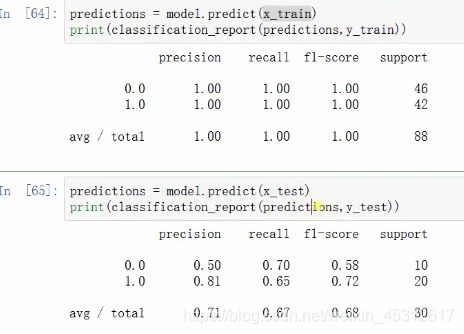
由此结果可得,数据在训练集中的准确率比在测试集当中的要高,原因是可能出现了过拟合的现象,由于非线性点集的划分边界较复杂,因此判定的决策树的分支也会比较多,决策树深度和复杂度都比较高,容易出现过拟合的现象,因此,若想提高最终划分集合的准确率,我们需要对决策树进行剪枝操作。
为此,我在这里进行了预剪枝的操作,不断调整和改进决策树中Max Depth(最大树深度)和Min Samples Split(内部节点再划分所需的最小样本数)这2个参数的值,最终得到了较好的分类结果。
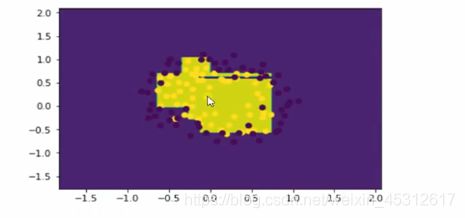
六、 优缺点总结(第一部分也有,此处再次总结)
经过对上述几种算法分类的探究实践,可以得出决策树模型的优缺点如下:
优点:
(1)速度快: 计算量相对较小,且容易转化成分类规则,只要沿着树根向下一直走到叶子节点, 沿途的分裂条件就能够唯一确定一条分类的谓词;
(2)准确性高: 挖掘出来的分类规则准确性高,便于理解,决策树可以清晰的显示哪些字段比较重要,即可以生成可以理解的规则;
(3)可以处理连续和种类字段;
(4)不需要任何领域知识和参数假设;
(5)适合高维数据。
缺点:
(1)对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征;
(2)容易出现过拟合现象;
(3)会忽略掉属性之间的相关性。