人工智能基础整理
人工智能基础整理
考前复习 随便整了一下
填空题
- 目前人工智能的主要学派有三家:符号主义、进化主义、连接主义
- 知识图谱本质上是结构化的语义知识库,是一种由节点和边组成的图数据结构,以符号形式描述物理世界中的概念及其相互关系
- 实现搜索过程的三大要素 搜索对象 扩展规则 目标测试
- 搜索的基本策略:盲目搜索 启发式搜索 随机搜索
- A*算法的特性可采纳性 : 如果问题有解,一定能找到最优解
- 遗传算法的基本定义:个体、适应性、群体、遗传操作(选择、交叉和变异)
- 遗传算法的基本流程:参数编码、初始群体设定、适应度函数设计、遗传操作设计和控制参数设定
- 知识表示是指将知识符号化并输入给计算机的过程和方法
- 逻辑表示法的优点 自然,明确,灵活,模块化
chapter3 搜索的基本策略
盲目搜索,启发式搜索,随机搜索
随机搜索,广度搜索,宽度搜索
盲目搜索算法又叫非启发式搜索,是一种无信息搜索
分支有界搜索也是一种深度优先搜索
启发式函数是一组映射函数
chapter4 图搜索策略
图搜索策略是一种在图中寻找解路径的方法
或图为搜索扩展时,可在若干分支中选择其一
与/或图为搜索拓展时,有可能要同时搜索若干分支,也可能在若干分支中选择其中之一
open表 考察节点
A*算法是当h(n)<=h*(n)时的A算法
A*算法的特性可采纳性 : 如果问题有解,一定能找到最优解
大的问题变换成若干子问题,… 分解到可以直接求解为止 问题的规约
chapter6 演化搜索算法
GA 遗传算法 是受遗传学中自然选择和遗传机制启发发展起来的一种搜索算法
遗传操作包括选择,交叉,重组
遗传算法基本流程 参数编码,初始种群设定,适应度函数设计,遗传操作设计,控制参数设定
选择是从当前群体中选出个体以生成交配池的过程
选择机制有基于适应值比例的选择和基于排名的选择和基于局部竞争机制的选择
交叉操作是将两个个体的遗传物质交换产生新的个体
变异是在个体中遗传物质被改变,它可以使运算过程中丢弃的个体的某些重要特性得以恢复
控制参数有位串长度,群体规模,交叉概率,变异概率
chapter10 知识表示与处理方法
知识分类方法有 过程式,陈述式
知识表示方法有 逻辑表示,产生式表示语义网络表示,连接词和量词表示,框架表示,过程式知识表示
逻辑表示法的优点 自然,明确,灵活,模块化
要使计算机具有智能,系统应具备 关于对象和物体的知识,事件,行为,元知识;
chapter15 人工神经网络
PDP模型 人工神经网络由8个方面的因素组成 处理单元,处理单元的激活状态,每个处理单元的输出函数,处理单元之间的接连模式,传递规则,激活规则,学习规则,系统运行的环境(样本集合)
人工神经网络在神经元及其连接和信息的存储和处理方面具有大脑的基本特征
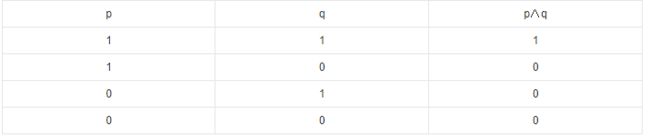
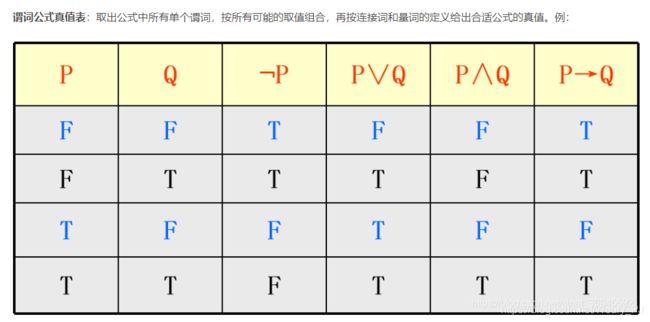
大题 真值表
大题 算法
宽度优先搜索算法
算法分析
ArrayList<int[]> open = new ArrayList<>();
ArrayList<int[]> close = new ArrayList<>();
open.add(new int[]{
0,0})
while(true){
1.取队首元素
2.执行操作,得到操作后的结果 x1,x2
3.判断x1,x2的状态
if(xi == 目标状态) break;
if(xi已经在close队列中){
// 不进行操作;
continue;
} else {
// 将xi加入open表中;
open.add(xi)
}
}
宽度优先搜索的优点是:若问题有解,则可找出最优解;
宽度优先搜索的缺点是:效率低,组合爆炸问题难以解决。
深度优先搜索的优点:节省大量时间和空间;
深度优先搜索的缺点:不一定能找到解。因为在无限 搜索树的情况下,最坏的情况可能是不停机。
水壶问题
给定两个水壶,一个可以装4升水,一个能装3升水,水壶上没有任何度量标记。有一水龙头可以用来往壶中灌水。问题是怎样在能装4升的水壶里面恰好只装2升水。
- 状态空间
- (x,y)
- x :4升
- y :3升
- (x,y)
- 定义操作
- x 倒入 y
// x:4 ; y:3 ; x倒入y if (x + y >= 3){ x -= 3 - y; y = 3; }else{ y = x + y; x = 0; } - y 倒入x
- x 倒满
- y 倒满
- x 清空
- y 清空
- x 倒入 y
倒啤酒问题
分啤酒问题:现有8升、5升、3升的容器各一个,均无任何度量标记,其中8升的容器装满啤酒,其他两个为空。要求用上述容器倒来倒去,分成两份4升的啤酒。
- 状态空间
- (x,y,z)
- x: 8升
- y :5升
- z : 3升
- (x,y,z)
- 定义操作
- x倒入y
- x倒入z
- y倒入x
- y倒入z
- z倒入x
- z倒入y
其中由于x是8升的,且啤酒总量为8升,所以倒入x的操作一定是可以全倒入的
// y 倒入 x
x += y;
y = 0;
y 倒入 z这种需要讨论
// y 倒入 z
if ( y + z >= 3){
y -= 3 - z;
z = 3;
}else{
z += y;
y = 0;
}
A* 算法分析
1. 创建open表和close表
2. 设S0位初始状态,Sg位目标状态
3. 将s0加入open表中,计算其评估值
while(true){
取出open表中评估值最小的节点S
将S加入close表中
if(S==Sg) break;
对S进行操作 (左右上下)得到S'
if(S'在close表中) continue;
else if(S'在open表中) 计算他们的评估值,将小的替换留下;
else 加入open表
}
优点: 一定能找到最优解,如果以搜索的节点各个为效率的评估原则,那么当h(n)单调递增的时候,其效率也不断增高
缺点: 当h(n)过低估计h*(n)的时候,其复杂性很高
评估函数的定义
八数码问题
f ( n ) = g ( n ) + w ( n ) f(n)=g(n)+w(n) f(n)=g(n)+w(n)
w ( n ) w(n) w(n) 采用曼哈顿距离来计算,或者取不一样的点的个数
野人传教士问题
m,c,b代表野人,传教士,船的位置(±1)
f ( n ) = g ( n ) + w ( n ) f(n)=g(n)+w(n) f(n)=g(n)+w(n)
w ( n ) = m + c − k ∗ b w(n) = m + c - k * b w(n)=m+c−k∗b
遗传算法
算法分析
- 编码
- 初始化种群
- 选择
- 交叉
- 变异
极大极小值问题
解码
public float[] decode(String num){
// 对输入的二进制编码转换为2个小数
float []result = new float[]{
0.0f,0.0f};
// 操作
int tmp_X = Integer.parseInt("",2)
return result;
}
选择
交叉
变异