免疫算法（01背包、TSP、函数极值）

免疫算法（01背包、TSP、函数极值）

​ 笔者是一位大一的萌新，这篇算法是自己查阅文献以及参考别人的博客再加上自身的理解写出来的。有错误的地方希望及时指正。这篇文章我使用的是Matlab，后续会给出python版本。以后会陆续出其他的优化算法以及人工智能算法，机器学习，深度学习等。

---

目录

1. 理论

2. 应用

3. 函数极值

4. TSP

5. 01背包

---

理论

背景介绍

在讲解免疫算法前，先来讲一下它的背景吧！在很久很久以前，1986年Farmal等人利用一组随机产生的微分方程建立起了人工免疫系统，再通过采用适应度阈值得过滤的方法去掉方程组中哪些不适合的微分方程，对保留的微分方程进行免疫系统的操作，也就是交叉、变异、逆转等等产生新的微分方程，不断迭代，直到找到一组最佳的微分方程为止。

免疫算法的概念

生物免疫系统	免疫算法
抗原	待优化的问题
抗体	可行解
亲和度	可行解的质量，相当于遗传算法的fitness
细胞活化	免疫选择
细胞分化	个体克隆
亲和度成熟	变异
克隆抑制	克隆抑制
种群刷新	种群刷新

算法主要包括以下几个模块：

(1) 抗原识别和初始抗体的产生，即审题和选择合适的抗体编码规则。

(2) 抗体评价。对抗体的质量进行评价，评价的准则包括抗体的亲和度和个体浓度，评价得出的优质抗体进行免疫操作。

(3) 免疫操作。利用免疫选择、克隆、变异、克隆抑制、种群刷新等算子模拟生物免疫应答中的各种免疫操作，寻求最优解。

参数和公式

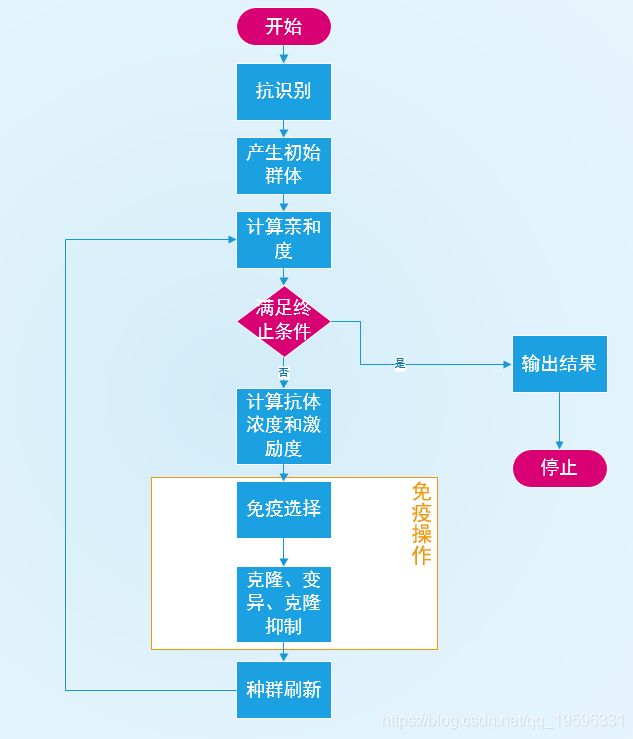
流程介绍

应用

函数极值

这个考虑了个体的浓度和亲和度。

clear;
close all;
clc;
Upper_1 = 5;
Lower_1 = -5;
Upper_2 = 5;
Lower_2 = -5;
m = 100;
Dimension = 2;
iter_max = 1000;
Pm = 0.7;
alfa = 1;
belta = 1;
iter = 1;
delta = 0.2;
produce = 10;
delta0_1 = 1*Upper_1;
delta0_2 = 1*Upper_2;
XX = rand(m,1)*(Upper_1 - Lower_1) + Lower_1;
YY = rand(m,1)*(Upper_2 - Lower_2) + Upper_2;
individual = [XX,YY];
for i = 1:m
    fitnesses(i) = func1(XX(i),YY(i));
end

for i = 1:m
    temp = zeros(m,1);
    for j = 1:m
        for k = 1:Dimension
            temp(j) = temp(j) + (individual(i,k)-individual(j,k))^2;
        end
        temp(j) = sqrt(temp(j));
        if temp(j) > delta
            temp(j) = 1;
        else
            temp(j) = 0;
        end
    end
    den(i) = sum(temp) / m;
end
Sim = alfa*fitnesses - belta*den;
[SortedSim,Index] = sort(Sim);
SortedIndividual = individual(Index,:);
while iter < iter_max
    
    
    
    for i = 1:m/2
        a = SortedIndividual(i,:);
        Na = repmat(a,produce,1);
        deta_1 = delta0_1 / iter;
        deta_2 = delta0_1 / iter;
        for j = 1:produce
            for ii = 1:Dimension
                if ii == 1
                    Na(j,ii) = Na(j,ii) + (rand-0.5)*deta_1;
                    if (Na(j,ii) > Upper_1) || (Na(j,ii) < Lower_1)
                        Na(j,ii) = rand*(Upper_1 - Lower_1) + Lower_1;
                    end
                else
                    Na(j,ii) = Na(j,ii) + (rand-0.5)*deta_2;
                    if (Na(j,ii) > Upper_2) || (Na(j,ii) < Lower_2)
                        Na(j,ii) = rand*(Upper_2 - Lower_2) + Lower_2;
                    end
                end
                
            end
        end
        Na(1,:) = SortedIndividual(i,:);
        for j = 1:produce
            Nafitnesses(j) = func1(Na(j,1),Na(j,2));
        end
        [SortedNafitness,Index] = sort(Nafitnesses);
        afitness(i) = SortedNafitness(1);
        NaSorted = Na(Index,:);
        aIndividual(i,:) = NaSorted(1,:);
    end
    
    
    for i = 1:m/2
    temp = zeros(m,1);
    for j = 1:m/2
        for k = 1:Dimension
            temp(j) = temp(j) + (aIndividual(i,k) - aIndividual(j,k))^2;
        end
        temp(j) = sqrt(temp(j));
        if temp(j) > delta
            temp(j) = 1;
        else
            temp(j) = 0;
        end
    end
    aden(i) = sum(temp) / (m / 2);
    end
    aSim = alfa*afitness - belta*aden;
    
    
    XX = rand(m/2,1)*(Upper_1 - Lower_1) + Lower_1;
    YY = rand(m/2,1)*(Upper_2 - Lower_2) + Upper_2;
    bIndividual = [XX,YY];
    for i = 1:m/2
        bfitnesses(i) = func1(bIndividual(i,1),bIndividual(i,2));
    end
    
    
    for i = 1:m/2
    temp = zeros(m,1);
    for j = 1:m/2
        for k = 1:Dimension
            temp(j) = temp(j) + (bIndividual(i,k) - bIndividual(j,k))^2;
        end
        temp(j) = sqrt(temp(j));
        if temp(j) > delta
            temp(j) = 1;
        else
            temp(j) = 0;
        end
    end
    bden(i) = sum(temp) / (m/2);
    end
    bSim = alfa*bfitnesses - belta*bden;
    
    NewIndividual = [aIndividual;bIndividual];
    NewSim = [aSim,bSim];
    [SortedNewFitnesses,Index] = sort(NewSim);
    SortedNewIndividual = NewIndividual(Index,:);
    SortedIndividual = SortedNewIndividual;
    trace(iter) = func1(SortedIndividual(1,1),SortedIndividual(1,2));
    iter
    
    
    iter = iter + 1;
end

BestIndividual = SortedIndividual(1,:);
BestValue = trace(end);
plot(trace);

function result = func1(x,y)
    result = 5*cos(x*y) + x*y+y^3;
end

TSP

这里只考虑了个体的亲和度没有考虑浓度，感兴趣的同学可以自己加上。（博主懒了，见谅）

clear;
close all;
clc;
n = 31;
x = rand(1,n)*100;
y = rand(1,n)*100;
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i~=j
            D(i,j) = sqrt(power(x(i)-x(j),2)+power(y(i)-y(j),2));
        else
            D(i,j) = 1e-3;
        end
    end
end
m = 200;
iter_max = 1000;
iter = 1;
produce = 10;
generation = zeros(m,n);
for i = 1:m
    generation(i,:) = randperm(n);
end
len = zeros(m,1);
for i = 1:m
    Route = generation(i,:);
    for j = 1:(n-1)
        len(i) = len(i) + D(Route(j),Route(j+1));
    end
    len(i) = len(i) + D(Route(n),Route(1));
end
[SortedLen,index] = sort(len);
SortedGeneration = generation(index,:);
while iter <= iter_max
    for i = 1:m/2
        a = SortedGeneration(i,:);
        ca = repmat(a,produce,1);
        for j = 1:produce
            p1 = floor(1+n*rand());
            p2 = floor(1+n*rand());
            while p1 == p2
                p1 = floor(1+n*rand());
                p2 = floor(1+n*rand());
            end
            temp = ca(j,p1);
            ca(j,p1) = ca(j,p2);
            ca(j,p2) = temp;
        end
        ca(1,:) = SortedGeneration(i,:);
        CaLen = zeros(produce,1);
        for j = 1:produce
            Route = ca(j,:);
            for k = 1:(n-1)
                CaLen(j) = CaLen(j) + D(Route(k),Route(k+1));
            end
            CaLen(j) = CaLen(j) + D(Route(n),Route(1));
        end
        [SortedCaLen,index] = sort(CaLen);
        SortedCa = ca(index,:);
        aGeneration(i,:) = SortedCa(1,:);
        aLen(i) = SortedCaLen(1);
       
    end
    blen = zeros(m/2,1);
    for i = 1:m/2
        bGeneration(i,:) = randperm(n);
        Route = bGeneration(i,:);
        for j = 1:(n-1)
            blen(i) = blen(i) + D(Route(j),Route(j+1));
        end
        blen(i) = blen(i) + D(Route(n),Route(1));
    end
    Generation = [aGeneration; bGeneration];
    len = [aLen'; blen];
    [SortedLen,index] = sort(len);
    SortedGeneration = Generation(index,:);
    trace(iter) = SortedLen(1);
    iter
    iter = iter + 1;
end
plot(trace)

01背包

这里只考虑了个体的亲和度没有考虑浓度，感兴趣的同学可以自己加上。（博主懒了，见谅）

clear;
close all;
clc;
n = 50;
V = 1000;
u = [80 82 85 70 72 70 66 50 55 25 50 55 40 48 50 32 22 60 30 32 40 38 35 32 25 28 30 22 25 30 45 30 60 50 20 65 20 25 30 10 20 25 15 10 10 10 4 4 2 1];

p = [220 208 198 192 180 180 165 162 160 15 8 155 130 125 122 120 118 115 110 105 101 100 100 98 9 6 95 90 88 82 80 77 75 73 72 70 69 66 65 63 60 58 56 5 0 30 20 15 10 8 5 3 1];

m = 100;
produce = 10;
possibility = 0.5;
Generation = zeros(m,n);
iter_max = 500;
iter = 1;
weight = zeros(m,1);
value = zeros(m,1);
for i = 1:m
    for j = 1:n
        if rand > possibility && weight(i)+ u(j) <= V
            Generation(i,j) = 1;
            weight(i) = weight(i) + u(j);
            value(i) = value(i) + p(j);
        end
    end
end
[SortedValue,index] = sort(value,1,'descend');
SortedWeight = weight(index);
SortedGeneration = Generation(index,:);
while iter <= iter_max
    for i = 1:m/2
        a = SortedGeneration(i,:);
        
        Ca = repmat(a,produce,1);
        
        for j = 1:produce
            p1 = floor(1+n*rand());
            if Ca(j,p1) == 0
                maxTime = 100;
                Time = 1;
                while u(p1) + SortedWeight(i) > V && Time <= maxTime
                    p1 = floor(1+n*rand());
                    Time = Time + 1;
                end
                if Time <= maxTime && u(p1) + SortedWeight(i) <= V
                    Ca(j,p1) = 1;
                end
            else
                Ca(j,p1) = 0;
            end
        end
        Ca(1,:) = SortedGeneration(i,:);
        CaValue = zeros(produce,1);
        CaWeight = zeros(produce,1);
        for j = 1:produce
            Route = Ca(j,:);
            for k = 1:n
                if Ca(j,k) == 1
                    CaValue(j) = CaValue(j) + p(k);
                    CaWeight(j) = CaWeight(j) + u(k);
                end
            end
        end
        [SortedCaValue,index] = sort(CaValue,1,"descend");
        SortedCaWeight = CaWeight(index,:);
        SortedCa = Ca(index,:);
        aGeneration(i,:) = SortedCa(1,:);
        aValue(i) = SortedCaValue(1);
        aWeight(i) = SortedCaWeight(1);
    end
    bGeneration = zeros(m/2,n);
    bValue = zeros(m/2,1);
    bWeight = zeros(m/2,1);
    for i = 1:m/2
        for j = 1:n
            if rand > possibility && bWeight(i)+ u(j) <= V
                bGeneration(i,j) = 1;
                bWeight(i) = bWeight(i) + u(j);
                bValue(i) = bValue(i) + p(j);
            end
        end
    end
    Genration = [aGeneration;bGeneration];
    Value = [aValue';bValue];
    Weight = [aWeight';bWeight];
    [SortedValue,index] = sort(Value,1,"descend");
    SortedGeneration = Genration(index,:);
    SortedWeight = Weight(index);
    trace(iter) = SortedValue(1);
    iter
    iter = iter + 1;
end
plot(trace)