若干种降维方法的实现与比较(PCA、MDS)

若干种降维方法的实现与比较(PCA、MDS)

新学到一种降维方式MDS，想到之前学过PCA但是也忘得差不多了，心想干脆这次来个包圆儿，一块再学习一遍，以后如果忘记还可以来这里再翻阅顺便编程给实现了，然后结合sklearn包里面提供的降维的方法进行了一些对比

---

---

1、降维

参考西瓜书里面的讲法，降维是从KNN算法这里引入的，如果大家对KNN算法还不太了解的话，其实就一句话，给定一个新样本，其类别是由原有样本中最接近的$k$个样本决定的。然后当原有样本数量的维数比较高，可能相隔非常远才有样本，这样跟近邻的概念有些背道而驰了。所以会考虑降低样本的维度，以增加样本在样本空间的密度。

维数灾难，curse of dimensionality，是困扰机器学习在一些场景适用性的一大问题。有的场景中数据分布非常稀疏、维数特别高，会带来距离比较难计算，结果不好解释等问题。所以降维，dimension reduction，是一个有效的途径。

那么为什么可以降维呢，这跟图片压缩差不多的意思，用更加少而精炼的部分来代替整体。降维就是通过一些数学的变换，将原始高位的属性空间转变为一个低维的子空间。样本虽然在观察的时候是高维的，但是跟学习任务相关的也许仅仅是某个低微分布，即高维空间的一个低维“嵌入”（embedding）。

---

2、MDS降维

2.1、原理介绍

MDS，多维缩放，Multiple Dimensional Scaling，一种经典的降维算法。

主要的特点是能够保持原始样本空间中样本之间的距离和降维后空间相等（或者十分近似）

由于自己也是第一次学习这个概念，还是把推导的过程给敲一遍吧，加深印象。

有$m$个样本在原始空间的距离矩阵为$D\in {\mathbb{R}}^{m\times m}$，第$i$行$j$列元素$dis{t}_{ij}$是样本$x_i$到$x_j$之间的距离。MDS的目的是获取样本在$d_1$维空间的表示$Z\in {\mathbb{R}}^{d_1\times m}$，且任意两个距离在$d_1$维空间的欧氏距离等于原始空间的距离，即$\Vert z_i-z_j\Vert =dis{t}_{ij}$。

令$B=Z^{T}Z\in {\mathbb{R}}^{m\times m}$为降维后样本的内积矩阵，$b_{ij}=z_i^T{z}_j$，有$$dis{t}_{ij}^2=\Vert z_i{\Vert }^2+\Vert z_j{\Vert }^2-2z_i^T{z}_j=b_{ii}+b_{jj}-2b_{ij}$$

为便于讨论，令降维后的样本$Z$被中心化，即${\sum }_{i=1}^m{z}_i=0$，显然矩阵$B$的行、列之和均为0。记矩阵的迹$tr(B)={\sum }_{i=1}^m\Vert z_i{\Vert }^2$，有$$\sum _{i=1}^{m}dis{t}_{ij}^2=tr(B)+m{b}_{jj}$$ $$\sum _{j=1}^{m}dis{t}_{ij}^2=tr(B)+m{b}_{ii}$$ $$\sum _{i=1}^m\sum _{j=1}^{m}dis{t}_{ij}^2=2mtr(B)$$

下面令$$dis{t}_{i\cdot }^2=\frac{1}{m}\sum _{j=1}^{m}dis{t}_{ij}^2$$ $$dis{t}_{\cdot j}^2=\frac{1}{m}\sum _{i=1}^{m}dis{t}_{ij}^2$$ $$dis{t}_{\cdot \cdot }^2=\frac{1}{m^2}\sum _{i=1}^m\sum _{j=1}^{m}dis{t}_{ij}^2$$

可以推导得到$$b_{ij}=-\frac{1}{2}(dis{t}_{ij}^2-dis{t}_{i\cdot }^2-dis{t}_{\cdot j}^2+dis{t}_{\cdot \cdot }^2)$$

上面的式子就可以从原矩阵$D$求取内积矩阵$B$

接下来就对矩阵$B$做特征值分解即可（特征值分解这里就不细讲了，可以参考线性代数里面相关章节的介绍）。选择最大的$d_1$个特征值构成的对角矩阵$\Lambda$，以及对应的特征向量构成的矩阵$V$，那么降维后的样本表示为$$Z={\Lambda }^{\frac{1}{2}}{V}^T\in {\mathbb{R}}^{d_1\times m}$$

其中${\Lambda }^{\frac{1}{2}}$，由于$\Lambda$已然是对角矩阵，所以只需要对对角的值取开平方即可。

---

算法流程

输入距离矩阵$D$，元素$dis{t}_{ij}$为样本$x_i$到$x_j$的距离，低维空间的维数$d_1$

过程：
1:计算$dis{t}_i,dis{t}_j,dis{t}_{avg}$，分别为各列、行、矩阵的距离
2:计算矩阵$B$
3:对矩阵$B$进行特征值分解
4:取$d_1$各最大特征值构成的对角矩阵，找到对应的特征向量矩阵

输出降维的各个坐标

---

2.1、代码实现

其实实现也是挺简单的，当然后面的数学原理确实是有些复杂吼，但是流程上面已经写的蛮清楚了，只需要一步一步实现就好了

首先引入一些包

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

from sklearn.datasets import make_s_curve

接下来是主要的过程

## 数据
x, t = make_s_curve(2000, 0.1, random_state=42)
## 降维的维数
d1 = 2
## 距离矩阵
D = np.zeros(shape=(len(x), len(x)), dtype=np.float64)
for i in range(len(x)-1):
    for j in range(i+1, len(x)):
        D[i, j] = distance(x[i], x[j])
        D[j, i] = D[i, j]
        
# 计算D的列、行、整体均值
dist_i = D.mean(axis=1) # 行
dist_j = D.mean(axis=0) # 列
dist_avg = D.mean()

# 初始化矩阵B
B = np.empty(shape=D.shape, dtype=np.float64)
# 得到B
for i in range(len(B)):
    for j in range(len(B)):
        B[i, j] = -(D[i, j]**2 - dist_i[i]**2 - dist_j[j]**2 + dist_avg**2) / 2

# 求B的特征值和特征向量
val, vec = np.linalg.eig(B)
# 中间矩阵
m1 = np.diag(val[np.argsort(val)[-1:-3:-1]].real)
m1 = np.sqrt(m1)
m2 = vec[:,np.argsort(val)[-1:-3:-1]].real
# 降维后的矩阵
rs = np.dot(m1, m2.T).T

当然如果调用sklearn里面现成的包是很快的，见下面代码

from sklearn import manifold

mds = manifold.MDS(n_components=2, max_iter=100, n_init=1)  #建立MDS模型
y = mds.fit_transform(x) # 训练并返回结果

是不是很简洁！！！

2.3、绘图分析与对比

首先生成的样本数据如图所示

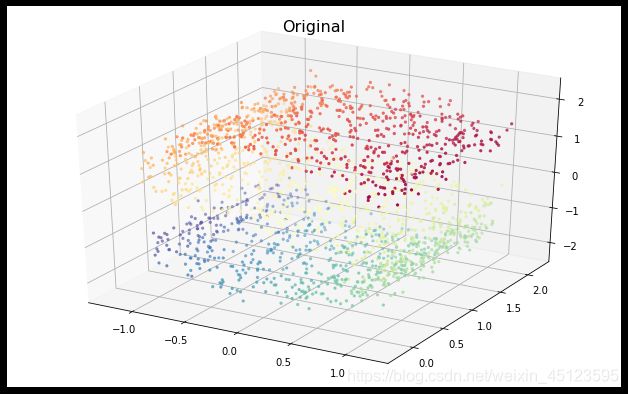
先看看用sklearn包降维得到的结果

可以看到在2000个样本点的情况下花了大概…18秒，还是挺长的哈，但是当我们去跑自己写的代码，emmm

自己的代码实现

好歹形状还是差不多的，甚至自己代码跑的还更正一点点，但是时间这里是封装模型的两倍多，优化做的还是不太够。然后在跑这个包代码的时候，发现每次运行的结果都是不一样的，我的直觉告诉我里面肯定有随机的影子，果不其然，给我抓了个正着，在MDS模型的参数中有一个random_state参数，但是当我兴致勃勃的随便设置了一个42之后，出现的结果还挺难看的，基本是看不出S的形状的。具体的原因如果有哪位小伙伴自己尝试之后发现了可以私信或者在下面评论哈。

3、PCA降维

关于PCA这里就不讲太多了，这个非常非常非常的常见，我们总是不假思索的提到降维就是主成分分析，他就是要寻找使得样本方差最大的投影方向。话不多说，直接上算法伪代码流程：

算法流程

输入样本集$D$，低维空间的维数$d_1$

过程：
1:对所有样本进行中心化：$x_i\leftarrow x_i-\frac{1}{m}{\sum }_{i=1}^m{x}_i$
2:计算样本的协方差矩阵$X{X}^T$
3:对矩阵$X{X}^T$进行特征值分解
4:取$d_1$各最大特征值构成的对角矩阵，找到对应的特征向量矩阵$W$

输出投影矩阵$W$

然后根据上面的步骤去写代码实现

## 中心化
delta = x.mean(axis=0)
x1 = x - delta
## 计算协方差矩阵
xie = np.dot(x1, x1.T)
## 对协方差矩阵进行特征值分解
val, vec = np.linalg.eig(xie)
# 投影矩阵
rs = vec[:,np.argsort(val)[-1:-(1+d1):-1]].real

好像也蛮简单的哦~

那如果用sklearn的包呢

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
rs2 = pca.fit_transform(x)

同样是非常简洁，接下里是结果的对比

首先先跑封装代码

结果非常Amazing啊，不得不说PCA是真的快，比起前面MDS花的十几秒来说

然后再跑自己实现的代码

貌似看起来也挺好的，不过自己写的跟模型训练的，跟上面MDS算法的结果好像有那么一点点不一样，但是好像问题也不太大，这个区分都是非常明显的，降维的效果是挺好的。可以看到上面的图片中写了一个Centralized，意思是已经进行过中心化的处理，也就是我们算法步骤的第一步，那我们想探究如果没有中心化呢，结果又是如何呢？

未进行中心化的结果就是…比较的难看，看不出优美的S曲线，但也能依稀看出PCA还是对原有的样本有些降维效果的，就是没有找到最合适的位置。

4、总结

上面介绍了两种降维的方法，供大家学习和参考。

文章原创不易，欢迎点赞收藏转发和打赏