对抗机器学习——Towards Evaluating the Robustness of Neural Networks

论文代码：

http://nicholas.carlini.com/code/nn_robust_attacks

论文motivation:

蒸馏网络说自己短小强撼，可以为目标网络模型提供很强的鲁棒性，号称自己能够把已经出现的攻击的成功率从95%锐减到0.5%。作者不信这个邪，于是基于L0,L2,L无穷范数提出三种新的攻击方法，尝试攻击蒸馏网络，而且还攻击成功了。而且作者认为，基于他们提出的三种攻击而生成的对抗样本具有很强的迁移性，新的防御模型应该要抵抗这些攻击。

作者还尝试使用不同的目标函数去生成对抗样本，实验发现不同的目标函数会大大影响攻击效果。===》白盒攻击，

===》 其实就是提出，攻击者还可以使用logit，而不是softmax后的数值来攻击。既然没有使用到softmax之后的概率，那么它自然可以把蒸馏网络攻击成功。

===》 例外提供使用tanh函数来平滑box约束。

蒸馏网络:Distillation

蒸馏网络一开始是提出来用于导师训练中把一个很大的导师模型降低为一个更小的蒸馏模型。蒸馏方法首先会以标准的方式训练得到一个导师模型，然后使用导师模型计算训练集里面所有样本的soft label,这里的soft label是指网络输出的各个类别的概率值（也就是softmax之后的输出结果），然后把整个softmax给的概率向量作为样本的标签变化整个训练集。这么做的好处是可以使得学生模型尽快的学习到导师的映射能力，相比hard label来说，soft label至少会包含更多的类别信息。

Defensive distillation 是指使用这种套路增强网络鲁棒性的一种防御方法。Defensive distillation与原始的distillation有两点不同：在defensive distillation中，学生模型和导师模型规模一样；defensive distillation会使用一个更大的蒸馏温度T，进而隐藏模型额外信息。

softmax函数是神经网络的最后一层，defensive distillation修改softmax 函数：

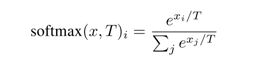
引入了一个温度参数T。显然有softmax(x,T)=softmax(x/T,1)。引入T的作用在于，当T很大的时候，T会把x之间的差异抹除掉，使得softmax(x,T)的输出接近于一个随机分布；而当T很小的时候，T会把x中最大的那个强调出来，其它分量给滤除掉。引入T后，各个分量之间的偏序关系还是保持不变的，即argmax softmax(x,T)=argmax softmax(x)。

举个例子：x=[1,2,3,4,5]

softmax(x) =[0.011656230956039607, 0.03168492079612427, 0.0861285444362687, 0.23412165725273662, 0.6364086465588308]

缩小10倍：
softmax(x/10)= [0.1621203478685732, 0.1791706936926544, 0.19801424004056153, 0.21883957945767904, 0.2418551389405318]

扩大10倍：
softmax(x*10)=[4.248161380306793e-18, 9.357198133414646e-14, 2.06106004620887e-09, 4.539786860886242e-05, 0.9999546000702375]

可以发现：
softmax(x)中各个量的差异很大，最后一个是最大的。
softmax(x/10)后，各个差异不大了。
softmax(x*10)后，各个量差异特别大，把最大的那个量的强调出来。
但是，这些结果中各个量的偏序关系是与x一致。

Defensive distillation 的步骤有四个：

• 1). 首先训练一个导师网络，最后一层softmax设置温度参数T。
• 2). 计算训练集里面的各个样本的soft label.把样本的y替换成soft label。
• 3). 训练学生网络，softmax也使用温度参数T。首先在训练学生网络的时候，受soft label的影响，输入到softmax之前的logit就被放大了T倍，
• 4). 学生网络在测试阶段，softmax中把温度设置为1。

最重要是这个学生网络中softmax把温度T设置为1。

测试的时候，温度T设置为1,相比于训练阶段，相似的x最后输入到softmax的值会扩大T倍，参考到上面的softmax(x*10)这个例子，这种扩大T倍会把softmax中正确标签的输出概率强制为1，而其他标签强制为0。这就是一个hard softmax了，很难获取梯度。想像一下，模型给出的probability是one hot的，那么$f(x+\delta )$和$f(x)$很有可能就是一样的，这样就根本没法指导对抗样本怎么生成。

一个想法：：：是不是，只需要hard softmax就可以了呢？也不用复杂的蒸馏了。
而logit就只会“扩大”T倍，这其实就是softmax(x,T)=softmax(x/T,1)的意思。测试阶段，温度设置为1，但是x还是x。

作者提出的方法

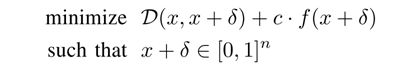
其中f()函数是一个很特别的函数，当C(x+δ)=t 的时候，f(x+δ)为非正数。

$C(x+\delta )$是分类器，$x+\delta \in [0,1{]}^n$是指作者把所有像素点的取值[0,255]线性变换到[0,1]了，然后要求对抗样本的每一个像素点都是合法的。
当这个目标函数取得最小值的时候，就会强迫 x+δ 这个对抗样本既使得分类错误、又使得$D(x,x+\delta )$ 最小，D是某个范数。

常数c是一个正数，用于衡量目标函数中两项的相对重要性。正是因为c是一个人为设置的参数，于是c的设置会显示出对这两项的偏好程度。然而，D,f是动态变化的，如果D,f的值不能与c反映的重要性相匹配就会出现很严重的问题。

作者使用了7种不同的f函数：

其中：

然后作者分别试了这些f函数下攻击的成功率，这里的攻击成功率是指能够从原始模型中找到对抗样本，这些模型还没被增强。

从结果来看，$f_6$ 效果最好。
为什么不同的f会有不同的效果，作者的理解是不同f的数值的scalar不一致，很难找到合适的c能够匹配f和D之间的比例。
例如：$\nabla f_1(x)$特别特别小，于是$f_1(x+\delta )-f_1(x)$ 特别小，那么x加上一个随机扰动对f的影响都巨小，没法指导这个扰动。要使得它发挥作用就只有把c取的特别大才行。

个人觉得，作者没有解释为啥f6/f7会好的那么多！f6和f2一样用了差值，但是f6的效果好上天，其根本原因在于：它使用了logit！而不是softmax后的probability！作者对于c的解释远不足以解释为啥f6/f7好。

作者的攻击

$L_2$ 攻击

$\frac{1}{2}(tanh(\omega )+1)$是 $x+\delta$，就是对抗样本，是为了自然而然的满足各维度取值在[0,1]的条件。$1/2(tanh(\omega )+1)-x$ 就是$\delta$ 。

$f(x^{\prime })=max(max\{Z(x^{\prime }{)}_i:i\ne t\}-Z(x^{\prime }{)}_t,-k)$是目标函数。这个函数就很有意思了。

我们把k设置为0 ，来分析。

$max\{Z(x^{\prime }{)}_i:i\ne t\}-Z(x^{\prime }{)}_t$ 表示把$Z(x’)$的所有非目标标签的logit中最大值减去目标标签的logit；如果x’被识别为目标标签t，那么$max\{Z(x^{\prime }{)}_i:i\ne t\}-Z(x^{\prime }{)}_t$ 是负的，于是$max(max\{Z(x^{\prime }{)}_i:i\ne t\}-Z(x^{\prime }{)}_t,0)=0$ 就没有对x’进行惩罚，但是如果x’被识别错误了，$max\{Z(x^{\prime }{)}_i:i\ne t\}-Z(x^{\prime }{)}_t$ 就是正数，x’就会被惩罚。

目标又是minimize 于是，那么没有被分类为目标标签的都会被惩罚。那么这里会不会一样有c的取值不能平衡D和f的问题呢？？ 这种方法最起码是更靠谱的，它相当于是在平衡∆x 和∆f(x)，而原来的函数是在平衡∆x和f(x)。个人认为f是一个差分，这个差值会比原来值更好一些？？？===》如果能设计出一个对F,D进行归一化的方法是不是也可以。

差值不是它能攻击蒸馏网络成功的主要原因。使用Logit才是！！！！！

$L_0$ 攻击

L_0攻击是指改动的像素个数最小的攻击。L0不可导，于是作者的方法是：一步步的找到那些对分类结果影响很小的像素点，然后固定这些像素点（因为改了它们也没有什么作用），直到无法再找到这样无影响的像素点了。

假设原图是x,L2攻击找到的对抗样本是$x+\delta$,于是计算$g=\nabla f(x+\delta )$,求得每个像素点的偏导。然后找出 $i=argmi{n}_i{g}_i{\delta }_i$,再把这个像素点丢掉。持续这个过程，直到L2攻击再也找不出样本了，此时剩下那些像素点就是必须得改的L0对抗样本。

$L_{\infty }$攻击

$L_{\infty }$也是不可导的，于是作者想出让δ的所有值都小于τ,然后逐步让τ越来越小，直到找不到对抗样本为止。