深度强化学习落地方法论(6)——回报函数篇
目录
- 前言
- 非要手工设计吗?
- 主线reward和稀疏回报问题
- 目标分解和辅助reward
-
- 目标分解实例
- 杜绝异常行为
-
- 贪婪
- 胆怯
- 鲁莽
- Reward Shaping
- Optimal Reward Problem
- 总结
- 参考文献
前言
回报函数(reward)设计在DRL应用中是极其重要的一环,通过将任务目标具体化和数值化,reward就如同一种特殊语言,实现了目标与算法之间的沟通,算法工作者在这里面承担了翻译的角色,翻译的好坏体现了其对任务逻辑的理解深度,决定了agent最终是否能学到期望的技能,并直接影响算法的收敛速度和最终性能。结合上一篇的内容,我们知道DRL算法中reward负责引导神经网络挖掘状态信息中的决策相关因素并经过提炼后用于action的计算生成。既然reward设计这么重要,想必分析起来又会是像状态空间那样的长篇大论吧。AI时代有了深度神经网络,也不缺数据和算力,难道这点人工就不能省下来吗?
非要手工设计吗?
鉴于强化学习算法对优秀reward函数设计的依赖,学术界提出了很多方法改善这一状况。比如逆向强化学习,利用expert demonstration(专家示范)学习到reward函数,再用这个reward函数训练RL策略。此外,还有一大堆模仿学习的方法,干脆抛开reward直接拟合专家策略。以上方法的前提是要有专家数据,不具备普适性,这里就不多说了。
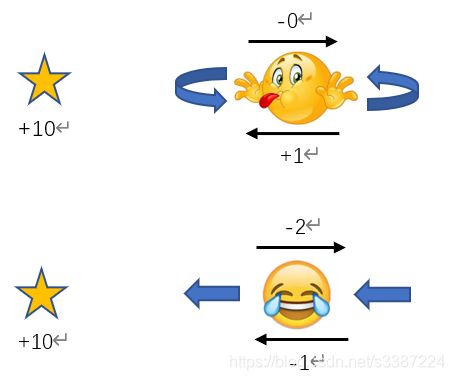
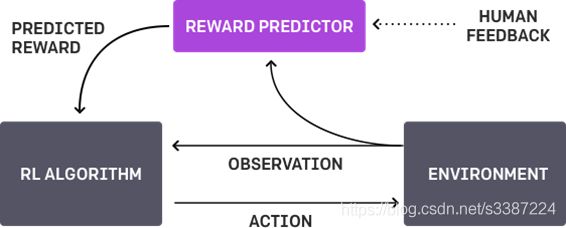
近年来学术界有个趋势,希望通过深度神经网络自动学习reward函数,从而代替手工设计。其中一篇比较有代表性的工作[1],在传统Actor-Critic框架的基础上,又增加了一个Reward网络,输入当前的状(state)和动作(action),输出这一步的reward值。Actor和Critic网络都依据最新的reward网络输出进行优化,而reward网络则依据人类(Supervisor)的喜好用有监督的方式进行更新,具体方法是周期性地采集一些episode片段并成对地让人类观看,后者反馈更喜欢哪个片段,再由reward网络拟合这个二分类问题。这篇paper的思想我非常欣赏,现实生活中确实存在很多难以分解和量化的目标,比如让agent学会后空翻,reward就很难设计;有些目标虽然是本身是量化的,但过于笼统难以分解成具体的reward,此时这种方法就很有吸引力。

可惜啊~~~,我们在现实中遇到的需求不大可能是第一种情况,比起“不能做→能做”,工业界更喜欢“能做→做得更好”,一般都会给出一个明确的指标用来最大化或最小化。假如这个指标能通过少量采样统计出来或体现出优劣关系,那就适合采用这种方法自动学习reward函数,而且不需要人的介入,全程自动化进行。但如果这个指标必须通过大量采样才能统计出来或者获得可靠的优劣关系,该方法的效率就非常低了,这种情况下就得老老实实地手工设计reward,走传统DRL路线了。
主线reward和稀疏回报问题
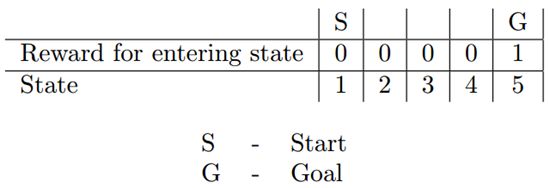
当我们拿到一个任务目标,往往能够简单分析就能找出与该目标紧密联系的主线事件,比如小车到达终点的任务中“到终点”就是这样的事件,拳皇里“KO”也是这样的事件,超级马里奥中“通关”还是这样的事件。此时我们就有了第一个reward项,我把它称之为主线reward,一般是正奖励,当主线事件发生时即反馈给agent。理论上,只要有主线reward就可以用强化学习算法进行训练了。在很多简单任务中,agent在探索过程中靠误打误撞就能以一定概率遇到主线事件,通过正反馈尝到甜头后通过更新policy逐渐提升得到奖励的概率直至收敛。可是当问题稍微复杂一些,通过随机方式探索到主线事件(正样本)的概率变得很低,而强化学习算法本身的数据效率不高,只靠这些少得可怜的正样本,算法难以收敛或收敛很慢。下面我引用伯克利RL大神Pieter Abbeel的课程CS294-40中的例子具体说明。
在上图中agent从最左端起始位置S处出发(state=1),目标是到达最右端的G位置(state=5),允许的动作包括向左一格和向右一格。在图中的reward系统下,agent只有到达G才能得到1分的奖励(主线reward),其他状态都没有任何反馈,那么仅靠随机探索agent是很难到达G的,因为中间缺乏有效信号来指导agent向正确的方向前进。在强化学习中,这一类问题被称作稀疏回报问题(Sparse Reward Problem),一直都是DRL领域研究的热点。显然,只定义了主线reward的任务几乎都是稀疏回报问题,对数据效率低下的RL算法而言,学习难度是很大的。
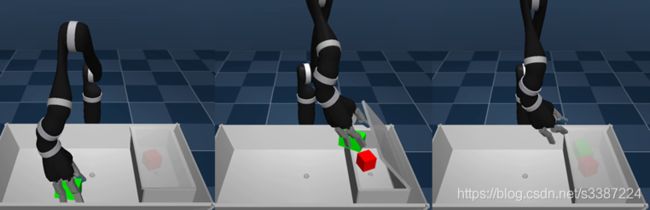
当稀疏回报问题遇上高难度探索(Hard Exploration)问题,DRL算法收敛更是难上加难,几乎是不可能完成的任务。比如让机器人学会打开盒子,抓起木块放到盒子里,然后再把盒子盖上,如果只在成功完成这一系列动作的时候才给出奖励,那么用一般的DRL算法和探索策略根本不可能学会目标技能,因为正样本产生的概率跟闭着眼用针尖扎到平面上一点的概率差不多,可以认为是0。
针对稀疏回报问题,学术界提出了很多方法,比如通过鼓励agent探索未见过的状态,提高正样本利用率,或者干脆用遗传算法或进化策略代替RL学习policy网络。这些方法不在本篇的讨论范围内,我们关心的是如何通过reward设计本身来规避稀疏回报问题,并尽可能提高训练效率和最终性能。
此外,联系上一篇状态空间设计的内容,由于主线事件通常难以一蹴而就,大部分状态信息相对于主线reward也就都属于间接相关信息,这也从另一个角度解释了为什么稀疏回报下算法训练难度高。
目标分解和辅助reward
既然只有主线reward不行,我们接下来就要将原始任务目标进一步分解成子目标,并分别给予合理的奖励或惩罚,从而达到引导agent趋利避害提高主线事件发生概率的目的,学术界一般称该过程为credit assignment,credit意译过来就是功劳,说的是某个子目标在达成总目标的过程中起了多大作用,是正向作用还是负向作用。这些子目标对应的reward可以称之为辅助reward,它们使reward不再稀疏。通常情况下,为了保证主线奖励的核心地位和吸引力,各种辅助reward的绝对值都设得相对较小,以免喧宾夺主。
目标分解实例
Agent在环境中探索时需要获得反馈,即刚刚的决策好不好,反馈越及时学得越快,理想情况是每一步都有反馈。以小车导航到终点的应用为例,除了抵达终点+10分,如果每次靠近终点也+1分,那么小车在抵达终点之前就学会主动靠近终点,这样探索到抵达终点的概率也大大提高了,RL算法收敛速度自然会加快。
除了抵达终点,小车还要避免与障碍物和其他小车发生碰撞,我们还要对碰撞事件做出惩罚。为了使agent更好地学会避免碰撞,我们除了对已经发生的碰撞事件给予惩罚,还可以再增加一个预防式的靠近惩罚,并利用状态空间里的直接相关信息——distance to nearest neighbor,提高算法学习效率,具体可以参考上一篇博客。
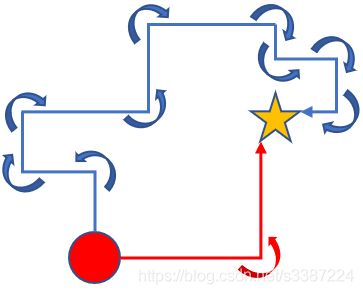
辅助reward的设计建立在对任务逻辑的深刻分析和理解之上,有很多细节都会对最终目标的实现产生正向或负向的影响,值得我们深入挖掘。比如,为了使小车尽快到达终点,就要求少绕路,而绕路的典型表现是转弯多,于是可以增加对转弯的惩罚。类似这样的链式思考有助于找到更好的辅助reward,帮助降低学习难度和提升最终性能。
此外,由于将最终目标分解成了子目标,在设计对应辅助reward时往往很容易找到与之即时联动的直接相关状态信息,或者相关性较强的间接相关信息。事实上,我们每设计一个reward项,就应该回过头去检查状态空间中是否包含了直接或间接相关信息,已经包含的信息是否足够高效(直接),有没有改进的空间。
杜绝异常行为
OK,让我们来捋一捋目前的reward项:抵达奖励,靠近终点奖励,碰撞惩罚和转弯惩罚。Reward项一多,我们就要特别注意它们之间的相对大小。首先,应该避免某个(些)reward项的绝对值过大,以至于淹没其他reward项的影响,必要时应使用系数加以调控;其次,应该避免reward项的不合理取值及多项reward之间的不合理相对大小,导致agent学到异常行为。因为不合理reward造成的常见异常行为主要包括三种类型:贪婪、胆怯和鲁莽,怎么感觉我在说炒股呢~~~
贪婪
靠近终点奖励使reward变稠密了,但这样做就够了吗?我们说过RL追求的是长期收益,事实上对小车来说收益最高的选择不是尽快抵达终点,而是不断重复“靠近-远离”的动作,如此一点点地累加,收益远超过抵达终点的一锤子买卖!很显然,agent钻了reward设计漏洞的空子,变得不思进取,贪得无厌。为了防止这种情况发生,我们还要对原地不动或远离终点的行为进行惩罚,而且相对于靠近奖励,扣分太少也不行,否则agent仍然会发现钻空子是划算的。一劳永逸的办法是,将靠近终点的正向奖励改成微小惩罚,绝对值小于原地不动或远离惩罚,这样做的好处是不仅不给agent钻空子的机会,而且还能督促小车尽快向终点行驶。
再比如在蒙特祖玛的复仇中,要想通关(主线事件,+10)必须先吃到钥匙,为了鼓励agent吃钥匙我们还可以为这个子目标提供专门的奖励(+1)。这种情况下房间只有一把钥匙还好,但如果到处都是钥匙呢?Agent很可能会变得乐不思蜀,一直留在房间里找新的钥匙,忘记通关这回事了。如果真是这样,那就不如不设吃钥匙奖励,只保留主线奖励,由Agent自己去发掘通关与吃钥匙之间的内在联系。


实际上,除了主线reward应该提供正向奖励以外,其他辅助reward最好都设置为惩罚项。除非某个子目标与主线事件之间存在强关联,而且该子目标的达成是一次性的或者数量可控,否则不应轻易设置额外奖励项,因为这样很容易诱导agent学习到短视的贪婪策略,只捡芝麻,不要西瓜。
胆怯
与贪婪相反的另一个异常行为是胆怯,如果惩罚项很多且绝对值相对于主线reward太大,那么agent在探索过程中会收到大量负反馈,从而变得畏首畏尾,学习到各种意想不到的“绥靖”策略。比如在小车到终点的例子中,假如碰撞惩罚和转弯惩罚绝对值过大,agent有可能宁愿选择原地不动,这是因为训练初期policy很差,需要经历大量转弯和碰撞后才可能出现主线事件(到达终点),而收到的负反馈完全湮没了主线奖励,因此在agent看来原地不动的长期累计收益暂时不比到终点差,尽管只是暂时的,但agent很可能陷在这个局部最优里出不来了。

在上述情况下,你会发现只需要将惩罚项绝对值减小,突出主线奖励的影响,其他什么也不用干,DRL模型就能顺利收敛了。当然,还可以适当降低折扣因子,让agent变成“近视眼”,更多关注眼前利益,忽略长期的负收益期望(靠后的负反馈都被折扣掉了),只要agent“迈开腿”出来探索,就有更大可能遇到主线事件,并在主线reward的奖励下学习到目标技能。折扣因子的设置技巧我将在训练篇中详细介绍。
鲁莽
鲁莽行为指的是reward中针对某个不希望出现的事件的惩罚太小,被其他reward项盖过,导致agent无法学到主动规避该事件或者权衡利弊后仍然选择接受该事件的惩罚以换取更大收益。比如碰撞惩罚相对于远离惩罚过小,小车可能为了尽快到达终点宁愿撞到其他小车上也不愿意绕远。
Reward Shaping
把任务目标分解得足够细,又避开了上述各种坑,这样就完美了吗?并没有~~~如果你读过Andrew Ng在2002年发表的关于reward shaping的paper,你就会发现还可以让RL算法收敛得更快一些。Reward shaping技术的证明这里就不赘述了,喜欢手推公式的朋友可以去读原著。我大概说下原理,在原有reward基础上增加一项shaping reward,该项代表某种势能函数,与最终目标的差距决定了势能大小。对于我们上一节举过的例子,如果把reward修改为下图中的形式,agent每向右移动一格都会获得奖励,且离G越近奖励越高,那么agent就很容易被引导到G位置,从而大大加速算法收敛。

Ng从理论上证明了理想势能函数就是V(s),这很好解释,我们前边说过V(s)是对长期收益的期望,policy就是根据它优化的,如果一开始就把完美的V(s)提供给小车,那也就不用学了。对小车到终点的应用而言,用小车当前位置与终点的距离作为势能函数,增加一个惩罚项 − α ⋅ d i s t -\alpha\cdot dist −α⋅dist,离终点较远时惩罚得多一些,较近时惩罚得小一些,这样就能起到reward shaping的作用。此外,参考上一篇状态空间设计的内容,你会发现增加的惩罚项可以与状态空间中描述小车与终点相对位置的信息即时联动,从而使后者由间接相关信息转变为直接相关信息,这就从另一个角度解释了reward shaping为什么能提高算法训练的效率。

Optimal Reward Problem
看到这里你可能会问,针对特定任务,比如小车导航到终点,是否存在一组最优reward使得DRL算法在同等条件下收敛最快、性能最高?答案是肯定的,但要想找到它是困难的,该问题在学术界被称为Optimal Reward Problem(ORP),解决方案包括暴力搜索[2]、基于在线策略梯度的PGRD [3]、分层强化学习[4]、遗传算法[5]、Bayes方法[6]等等,有兴趣的朋友可以找来相关paper读一读,相关参考文献我列到最后。
总结
总结一下,reward设计的原则是:尽可能稠密(最好每步都有反馈),能够反映任务目标/子目标逻辑,与状态空间相呼应,控制好各项取值和相对大小,避免异常行为,适时采用reward shaping。当算法选择好,动作空间定义好,状态空间和回报函数都设计好,接下来就该进入训练环节了。
参考文献
[1] Christiano, P. F.; Leike, J.; Brown, T. B.; Martic, M.; Legg, S.; and Amodei, D. 2017. Deep Reinforcement Learning from Human Preferences. Neural Information Processing Systems: 4299-4307.
[2] Sorg, J.; Singh, S. P.; and Lewis, R. L. 2010. Internal Rewards Mitigate Agent Boundedness. International Conference on Machine Learning: 1007-1014.
[3] Sorg, J.; Lewis, R. L.; and Singh, S. P. 2010. Reward Design via Online Gradient Ascent. Neural Information Processing Systems: 2190-2198.
[4] Bratman, J.; Singh, S. P.; Sorg, J.; and Lewis, R. L. 2012. Strong Mitigation: Nesting Search for Good Policies within Search for Good Reward. Adaptive Agents and Multi Agents Systems: 407-414.
[5] Niekum, S.; Barto, A. G.; and Spector, L. 2010. Genetic Programming for Reward Function Search. IEEE Transactions on Autonomous Mental Development 2(2): 83-90.
[6] Hadfield-Menell, D.; Milli, S.; Abbeel, P.; Russell, S.; and Dragan, A. D. 2017. Inverse Reward Design. Neural Information Processing Systems: 6765-6774.