利用pytorch搭建你的神经网络
利用pytorch搭建你的神经网络
1、理解pytorch中Numpy、Tensor与Variable
Numpy是一个数学库,主要用于数组的计算。而我们使用Numpy也是可以手动去编写神经网络进行反向传播深度学习的,但是有两个问题,一是利用Numpy手动去编写神经网络很繁琐,代码量较大,不利于大规模开发;二是Numpy是利用CPU运算,而无法直接使用GPU加速计算。
Tensor,中文名叫张量,如果一个物理量,在物体的某个位置上只是一个单值,那么就是普通的标量,比如密度。如果它在同一个位置、从不同的方向上看,有不同的值,而且这个数恰好可以用矩阵乘观察方向来算出来,就是张量。几何代数中定义的张量是基于向量和矩阵的推广,通俗一点理解的话,我们可以将标量视为零阶张量,矢量视为一阶张量,那么矩阵就是二阶张量。
在PyTorch中,Tensor是重要的数据结构,可认为是一个高维数组。Tensor和Numpy中的ndarrays类似,但Tensor可以使用GPU进行加速计算。PyTorch中有许多不同的方法可以创建Tensor或者将Numpy数据转换成Tensor。
PyTorch为了实现GPU加速功能,引入了Tensor,为了实现自动求导功能引入了Variable。顾名思义,Variable就是 变量 的意思。实质上也就是可以变化的量,区别于int变量,它是一种可以变化的变量,这正好就符合了反向传播,参数更新的属性。在torch中的Variable就是一个存放会变化的值的地理位置。里面的值会不停发生变化,就像一个装鸡蛋的篮子,鸡蛋数会不断发生变化。那谁是里面的鸡蛋呢,自然就是torch的Tensor了(换言之就是torch是用tensor计算的,tensor里面的参数都是variable的形式),如果用Variable进行计算,那返回的也是一个同类型的Variable。
Varibale对Tensor进行了封装,包含三个属性:
- data:存储了Tensor,是本体的数据
- grad:保存了data的梯度,本事是个Variable而非Tensor,与data形状一致
- grad_fn:指向Function对象,用于反向传播的梯度计算之用
并且tensor不能反向传播,variable可以反向传播。在Variable计算时,它会逐渐地生成计算图。这个图就是将所有的计算节点都连接起来,最后进行误差反向传递的时候,一次性将所有Variable里面的梯度都计算出来,而tensor就没有这个能力。
import numpy as np
import torch
from torch.autograd import Variable
np_data = np.arange(6).reshape((2, 3))#得到numpy数组
torch_data = torch.from_numpy(np_data)#numpy数组转为tensor张量
tensor2array = torch_data.numpy()#tensor张量转为numpy数组
tensor = torch.FloatTensor([[1,2],[3,4]])#创建Tensor
variable = Variable(tensor, requires_grad=True)#创建variable
v_out = torch.mean(variable*variable)
v_out.backward()
print('v_out:\n', v_out)
'''
v_out:
tensor(7.5000, grad_fn=)
'''
print('variable.grad:\n',variable.grad)
'''
variable.grad:
tensor([[0.5000, 1.0000],
[1.5000, 2.0000]])
'''
print(variable.data)
'''
variable.data:
tensor([[1., 2.],
[3., 4.]])
'''
print('variable.grad_fn:\n', variable.grad_fn)
'''
variable.grad_fn:
None
'''
Pytorch与Numpy类似,具有很多操作方法,详见:https://pytorch.org/docs/stable/torch.html
backward()的理解:
2、实例1:利用pytorch搭建神经网络用于回归或者分类
2.1导入库与数据
主要导入torch库,导入的数据类型应该是tensor,详见实例1代码。
2.2搭建多层神经网络
搭建多层神经网络有常用方法,将神经网络层和激活函数分别写,也可以利用sequential快速搭建神经网络,按照“输入——输出”次序,将神经网络的隐藏层和激活函数一行行写出,笔者推荐快速搭建法便于理解和使用。下面的代码是通过两种方法搭建一个三层神经网络,输入节点为1,隐藏层节点为10,输出节点为1,激活函数采用ReLU函数。

import torch
import torch.nn.functional as F
# 2.2.1常用方法
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_feature, n_hidden) # hidden layer
self.predict = torch.nn.Linear(n_hidden, n_output) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
net1 = Net(1, 10, 1)
# 2.2.2快速方法Sequential(推荐)
net2 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
2.2.3激活函数
在神经网络搭建中,可供选择的激活函数有很多,详情可见pytorch官网关于激活函数的描述,点击此处即可跳转。这里主要介绍常用的几个:
(1)ReLU
其函数表达式为:Relu=max(0,x)。在x<0时,取0;在x>=0时,取x的值。ReLU虽然简单,但却是最常用的激活函数。它的计算速度和收敛速度远高于sigmoid和tanh,但是ReLU函数的确存在一些问题,比如:ReLU的输出不是zero-centered、Dead ReLU Problem等。
sigmoid的表达式:
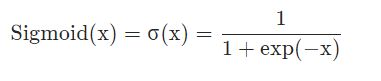
可以看出,当x由负无穷到正无穷变化时,函数值由0向着1逐渐增加。sigmoid函数在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失,其中梯度爆炸发生的概率非常小,而梯度消失发生的概率比较大,因此应用越来越少。

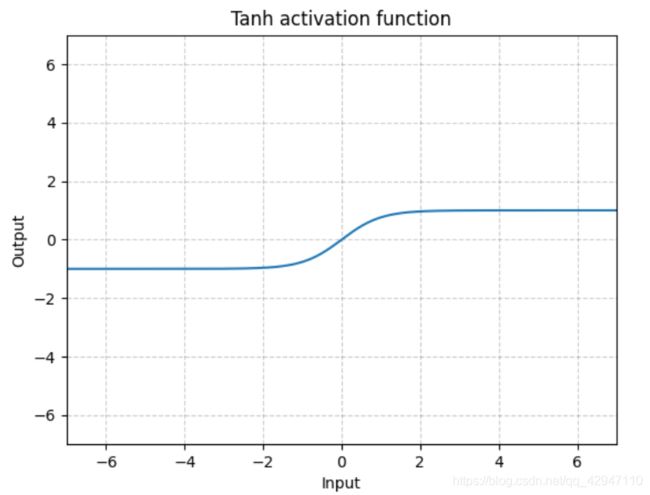
(3)tanh
tanh函数解决了Sigmoid函数的不是zero-centered输出问题,但是仍然存在梯度消失(gradient vanishing)的问题和幂运算的问题。其函数表达式如下:
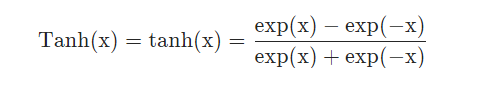](http://img.e-com-net.com/image/info8/66b174f412c1487a8915530faf4a1132.jpg)
2.3设置损失函数和优化器
2.3.1损失函数
2.3.2优化器
官网:https://pytorch.org/docs/stable/optim.html
2.4训练与批训练
批训练用于数据量较大,每次训练时占用的硬件内容较大,因此可以将数据分批次传入神经网络中进行训练。比如笔者之前进行过17万数据量的回归分析,因为直接将17万条数据传入网络进行处理需要的物理内容远远超过设备的内存,因此可以选择将数据分为17批次,每批1万数据量进行训练,会降低对物理内存的要求,节省训练时间。
示例代码:
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
dataset=torch_dataset, # 待训练的数据集
batch_size=BATCH_SIZE, # 每批次最小的数据量
shuffle=True, #在训练时是否将数据进行随机打乱
num_workers=2, # 处理数据时的线程数
)
def show_batch():
for epoch in range(3): # 训练次数,即将全部的数据训练多少次
for step, (batch_x, batch_y) in enumerate(loader): # 进行批训练,step是批次的序号
# 此处放置训练数据的代码
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
batch_x.numpy(), '| batch y: ', batch_y.numpy())
2.5保存(提取)神经网络
为了便于将训练过后的神经网络进行保存,这里提供一种方法,直接保存训练过后的神经网络的参数。这种方法与直接保存整个神经网络模型相比,会占用更少的空间。在提取较大的神经网络时,读取速度会比较快。
例如:
torch.save(net.state_dict(), 'net_params.pkl')#保存训练的神经网络net的参数
net.load_state_dict(torch.load('net_params.pkl'))#net为搭建的神经网络
实例1参考代码
#####################################实例1参考代码##############################
import torch
import torch.nn.functional as F
import torch.utils.data as Data
#2.1导入库与数据
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = x.pow(2) + 0.2*torch.rand(x.size())
torch_dataset = Data.TensorDataset(x, y)
#2.2搭建多多层神经网络
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden1, n_hidden2, n_output):
super(Net, self).__init__()
self.hidden1 = torch.nn.Linear(n_feature, n_hidden1) # hidden layer1
self.hidden2 = torch.nn.Linear(n_hidden1, n_hidden2) # hidden layer2
self.predict = torch.nn.Linear(n_hidden2, n_output) # output layer
def forward(self, x):
x = F.relu(self.hidden1(x)) # activation function for hidden layer
x = F.relu(self.hidden2(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
net = Net(1, 5, 2, 1)
#2.3损失函数与优化器
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)#优化器,lr学习效率
loss_func = torch.nn.MSELoss()#损失函数
loader = Data.DataLoader(
dataset=torch_dataset, # torch TensorDataset format
batch_size=50, # 每批训练50条数据
shuffle=True, # 训练时候随机打乱顺序
num_workers=2, # 使用2个线程
)
#2.4定义批训练函数
def show_batch():
for epoch in range(5): # 进行200次训练
for step, (batch_x, batch_y) in enumerate(loader):
prediction = net(x)
loss = loss_func(prediction, y)
optimizer.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
batch_x.numpy(), '| batch y: ', batch_y.numpy())
print('LOSS:', loss)
if __name__ == '__main__':
show_batch()
#2.5存取训练后神经网络的参数
torch.save(net.state_dict(), 'net_params.pkl')
net2 = Net(1, 5, 2, 1)
net2.load_state_dict(torch.load('net_params.pkl'))
print(net2.state_dict())
3、常用的神经网络
在深度学习和强化学习异常火热的今天,神经网络模型层出不穷,听过老师讲述,一种模型无论简单或者复杂,都有其优缺点和常用的应用领域。一种模型的效果好往往会伴随着其应用范围小和应用场景较少的特点,而有的模型虽然效果差一些但是其对环境的适应性会强一些。例如:卷积神经网络(CNN)常常用于计算机图像处理,循环神经网络(RNN)常用于自然语言处理等等。建议初学神经网络还是优先了解各个模型的应用领域和优缺点,鉴于笔者对于这些模型还没有到位的理解,这里推荐一篇文章:
一文看懂25个神经网络模型
望读者批评指正
参考文献(以下均为超链接,读者可以点击跳转):
1、[开发技巧]·PyTorch中Numpy,Tensor与Variable深入理解与转换技巧
2、PyTorch学习笔记(二):Tensor操作
3、PyTorch中的Variable变量详解
4、pytorch Variable变量
5、task4: 多层神经网络–pytorch实现
6、Pytorch之搭建神经网络的四种方法
7、【PyTorch】torch.nn.Module 源码分析
8、pytorch官网
9、常用激活函数(激励函数)理解与总结