基于python的简单KNN算法(K- Nearest Neighbor)的实现与改进
最近在自学python的数据分析,还想稍微蹭一蹭深度学习,于是不可避免地接触到了最简单的机器学习算法——KNN算法。该方法的思路非常简单直观:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
用人话说就是:如果要对一个样本进行分类,就看看这个样本周围都是些什么东西。要是跟样本比较接近的人是一群小混混,那么,这个样本估计比小混混也好不到哪儿去,要是跟样本比较接近的都是一群酒肉朋友,那样本估计就是朱一旦本旦了(非洲警告) 。
所以具体要怎么实现KNN算法呢?
其实,python的sklearn库中是内置了KNN算法的,我也尝试着把鸢尾花数据集放进去跑了一下,然而,随着硬盘的一声嗡鸣,计算结果一览无余,眼前的一切突然变得索然无味,进入了贤者模式的我开始反思自己的所作所为: 连这么一个简单的算法都要调库进行实现的我配敲代码吗?(调库的代码很无脑,所以我没有保留,但是我把有关的博客链接放到了文末,看官老爷们要是感兴趣的话可自行移步学习)
所以,我开始尝试自己自己实现KNN算法
算法的大体思路就是提取待分析样本的特征,然后将特征与原有的特征库进行比对,量化样本与原有数据之间的差距,找出与样本最接近的K个点,哪一类的点最多,这个样本归属于哪一类的概率也就越大
当然了,为了节省看官老爷们的时间,该调的辅助计算库还得调:)
from scipy.spatial import distance#这是为了简化计算,方便调用内置计算函数
import matplotlib.pyplot as plt #这是为了做一点基本的可视化图表
import numpy as np #这是因为np.array骚操作太多太快乐了
import operator #这个就厉害了,用途我后面再说
一、首先我得有个样本库,并对样本库的特征进行提取。但是特征提取可是一门大学问,作为还没有达到朋友圈平均水平的菜鸡本鸡只好用最简单的距离特征作为今天的主要测试材料:
好了,下面是我费尽九牛二虎之力提取(编造)的距离信息
#我的数据库,有亿点点寒酸
x1 = np.array([3,2,1,6,5,4])
y1 = np.array([104,100,81,110,105,103])
x2 = np.array([101,99,98,97,96,95])
y2 = np.array([10,5,2,1,3,1])
#为了让数据变得好看一点,同时便于计算,用坐标形式保存
#知道有些看官老爷们没仔细研究过numpy库,我在下面对我用的一些骚函数进行一下解释
A_data = np.concatenate((x1.reshape(6,1),y1.reshape(6,1)), axis = 1)
B_data = np.concatenate((x2.reshape(6,1),y2.reshape(6,1)), axis = 1)
#1、reshape函数,作用是对numpy数组进行维度的升降变化
#参数只有两个,分别是想让数组变成的行数以及列数
#2、concatenate函数,作用是灵活地对数组进行拼接
#原型大概长这样:concatenate((a1, a2, ...), axis=0, out=None)
#a1、a2...就是待拼接的数组
#out参数就是你想要输出的数组名
#axis参数就比较复杂了,简而言之,就是沿着axis所指定的轴进行操作
#最外层的是0轴,往内依次是1轴,2轴…
#待分类数据
x = np.array([18])
y = np.array([90])
#变成坐标形式
C_data = np.append(x,y)
A_size = A_data.shape[0]#求出目标点的组数
B_size = B_data.shape[0]#起码我得知道我的数据库有多大呀
这里对上面的一些迷惑操作进行一波解释:
-
为什么待分类数据就一个坐标我还要用三行语句去变换和赋值?
其实我写这个KNN算法是为了处理大量的数据并对大量样本进行分类的,但是我并没有那么多样本与数据,所以我只能假装我有很多的数据【facepalm】。那么在这个假设下,为了代码的简洁性以及执行的效率(毕竟python的执行效率在编程语言中是出了名的低,而KNN的计算量在机器学习算法里也是出了名的大),我将在后面的代码中尽量调用numpy库而非for循环进行计算
-
那么为什么你不能多编几个数据来扩大数据库的容量呢?
别问,问就是懒
-
axis参数到底怎么用?
详见https://blog.csdn.net/ksws0292756/article/details/80192926
(码龄六年的大佬的文章)
二、那么既然已经把数据库以及待检测样本处理好了,我们对数据稍微进行一下可视化处理:
scatter1 = plt.scatter(x1,y1,c='r',marker = 'v')#散点组合一
scatter2 = plt.scatter(x2,y2,c='b',marker = '*')#散点组合二
scatter3 = plt.scatter(x,y,c='k')#假装量很大的待分类数据
#先画个图出来看看
#看看待识别的数据大概在哪
plt.legend(handles=[scatter1,scatter2,scatter3],labels=['labelA','labelB','X'],loc='best')
plt.show()
画图效果如下:
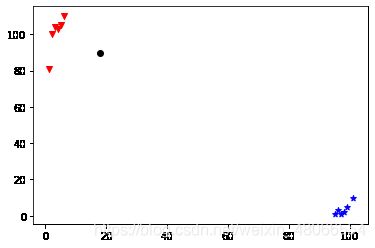
正如你们所见,我们的待分类数据应该是属于红色的A组。但我偏不使用肉眼可见法,我就是想给自己找麻烦【doge】。
三、于是,进行我们的下一步:对数据进行深加工,为接下来距离的计算打好基础
#首先,我们需要对我们的两类数据进行合并,合成一个大数据库
all_data = np.concatenate((A_data, B_data), axis = 0)
#只要你相信这是一个大数据库,那他就一定是一个大数据库
all_size = A_size + B_size
#其次,我们需要对我们数据库中的各组数据进行标记
mark = np.append(['A']*A_size, ['B']*B_size)
#然后,为了方便进行操作,把待分类数据点进行复制
np.tile(C_data,(all_size,1))
#tile 是瓷砖的意思,顾名思义,这个函数就是把数组像瓷砖一样铺展开来
#也就是将原矩阵横向、纵向地复制。
四、至关重要的一步,待分类点与数据库中各点距离的计算与表示
你可能以为,不就是一个简单的点与点之间的距离吗,那不是有手就彳亍
其实不然,我们平时所说的距离指的是欧氏距离,就是sqrt(x^2 + y^2)那个距离,但是实际上,表示距离还有很多种方式,具体如下:
#欧氏距离,就是我们最常用的距离
eu_dist = distance.cdist(example1, example2, "euclidean")
print("\n euclidean dist = \n", eu_dist)
#曼哈顿距离,指两个点在标准坐标系上绝对轴距的总和
cb_dist = distance.cdist(example1, example2, "cityblock")
print("\n cityblock dist = \n", cb_dist)
#切比雪夫距离,指两个点之间各坐标数值差绝对值的最大值
cs_dist = distance.cdist(example1, example2, "chebyshev")
print("\n chebyshev dist = \n", cs_dist)
#余弦距离,测量两个向量夹角的余弦值来度量他们之间的相似性
cos_dist = distance.cdist(example1, example2, "cosine")
print("\n cosine dist = \n", cos_dist)
#相关系数距离,相关系数越大距离越远
cl_dist = distance.cdist(example1, example2, "correlation")
print("\n correlation dist = \n", cl_dist)
#马氏距离,定义n维空间点与点间距离
ml_dist = distance.cdist(example1, example2, "mahalanobis")
print("\n mahalanobis dist = \n", ml_dist)
那么,说了这么多,我们到底要用什么距离进行计算呢?
emmmm,结果我还是用了欧氏距离没错我是屑
#返璞归真的欧氏距离
#这里没有用上面的distance,为什么呢
#因为numpy库太强了,骚函数太多,想着趁这个机会熟悉一下
eu_dis = (((C_data - all_data)**2).sum(axis = 1))**0.5
#还有一个好玩的黑科技函数
sort_index = eu_dis.argsort()
#这个函数的效果如下
#In:
#sort_index = eu_dis.argsort()
#Out:
#[ 1 5 2 4 0 3 6 10 7 11 8 9]
五、好了,距离都算完了,连排序都排好了,接下来我们确定k的值并输出结果
#今天的主角:K 终于登场了
k = 10
#为了使结果好看一点,我们使用字典来保存这个结果
rst = {
}
for i in range(k):
rst_mark = mark[sort_index[i]]
rst[rst_mark] = rst.get(rst_mark,0) + 1
#这个get()函数的作用是:返回rst_mark所对应的键值,
#若该键未指定值,则把第二个参数设定为值
#奇怪的黑科技增加了
#operator模块提供的itemgetter函数用于获取对象的哪些维的数据
rst_sort = sorted(rst.items(), key = operator.itemgetter(1), reverse = True)
#其实就是获取字典的键值并对其进行排序处理
#最激动人心的一步来了
print(rst_sort)
输出结果:
![]()
OHHHHHHHHHHHHHHHHHHHH
轻而易举的得出了答案!!!!
毫无疑问,我们的knn模型获得了巨大成功!!!!!!
.
.
.
.
.
.
.
.
.
.
.
.
但你以为这就完了吗?
敲完上述的最后一行代码,我本该使出我的成名绝技标志性后仰如释重负地瘫倒在椅背上,惬意的享受自己的小小成功带来的满足感,但是,真的就这么完了吗???
假如我的K值取的是12也就是整个数据库数据量的大小呢?
那么我得到的结果将是[ (‘A’, 6), (‘B’, 6) ]!
那这个knn模型的鉴别能力不就不复存在了吗?
六、针对以上问题,我想到了一个简单但也许有效的解决方法
为了既体现k的作用又解决上述问题,我对代码进行了一下改进
k = 10
sum = 0
for i in range(k):
sum = sum + eu_dis[sort_index[i]]
rst = {
}
for i in range(k):
rst_mark = mark[sort_index[i]]
rst[rst_mark] = rst.get(rst_mark,0) + eu_dis[sort_index[i]]/sum
rst_sort = sorted(rst.items(), key = operator.itemgetter(1), reverse = False)
print(rst_sort)
那么出来的结果会是什么样的呢?
k = 10:
![]()
k = 12
![]()
我来给你们解释下这个结果是什么意思哈:就是说,如果我们认为这个待分类样本的类别是A的话,我们犯错的几率是20.56%;而如果我们认为这个待分类样本的类别是B的话,我们犯错的几率是79.44%
其实,我只不过是对结果进行了一个小小的加权,这时候,k的值不仅影响精确度,并且直接关系到模型的计算量,并且,k的值越大,模型的精确度越高,而且结果也改变了原来一刀切的判断方式,而是变成了更严谨的概率,完美地解决了原来采用欧氏距离大小排序的弊端。所以。。。
快夸我【手动滑稽】
第三次写博文了,语言也从原来的c++变成了python,怎么说呢,我发现用给别人讲解的口吻去做自己的学习笔记会使我的效率变得出奇的高,所以这篇文章不仅是我的一篇学习笔记,更是对我这一两天学习成果的一次讲解,一次展示。当然,这篇博文也算不上是一篇合格的教学文章,因为里面包含着大量个人的自嗨元素,还请抱着研究交流想法进来的大佬们多多包涵。文章中或许还有许多不成熟,不详细甚至是不正确的地方,还请各位大佬不吝赐教,不才定然有则改之无则加勉。
好了,就BB这么多,大佬们评论区见:)