机器学习 特征选择篇——python实现MIC(最大信息系数)计算
机器学习 特征选择篇——python实现MIC(最大信息系数)计算
- 摘要
- python实现代码
- 计算实例
摘要
MIC(最大信息系数) 可以检测变量之间的非线性相关性,常用于特征工程中的特征选择,即通过计算各特征与因变量之间的MIC,从中挑选出对因变量影响较大的特征,剔除信息量较少的特征,从而使得用于建模的变量更具代表性。一般使用该方法时,需要有较大的数据样本。本文通过python实现了MIC(最大信息系数)计算,并将代码进行了封装,方便读者调用。
python实现代码
.x_num:在变量x方向上划分的区间数,可以指定最小和最大值,也可不指定
.y_num:在变量y方向上划分的区间数,可以指定最小和最大值,也可不指定
.cal_mut_info():由概率矩阵计算互信息
.divide_bin():由划分区间计算概率矩阵
cal_MIC():计算最大信息系数
用法:直接调用cal_MIC() 函数计算两个变量之间的MIC
# -*- coding: utf-8 -*-
# @Time : 2020/12/3 13:44
# @Author : CyrusMay WJ
# @FileName: MIC.py
# @Software: PyCharm
# @Blog :https://blog.csdn.net/Cyrus_May
import numpy as np
import logging
import sys
class CyrusMIC(object):
logger = logging.getLogger()
logger.setLevel(logging.INFO)
screen_handler = logging.StreamHandler(sys.stdout)
screen_handler.setLevel(logging.INFO)
formatter = logging.Formatter('%(asctime)s - %(module)s.%(funcName)s:%(lineno)d - %(levelname)s - %(message)s')
screen_handler.setFormatter(formatter)
logger.addHandler(screen_handler)
def __init__(self,x_num=[None,None],y_num=[None,None]):
self.x_max_num = x_num[1]
self.x_min_num = x_num[0]
self.y_min_num = y_num[0]
self.y_max_num = y_num[1]
self.x = None
self.y = None
def cal_mut_info(self,p_matrix):
"""
计算互信息值
:param p_matrix: 变量X和Y的构成的概率矩阵
:return: 互信息值
"""
mut_info = 0
p_matrix = np.array(p_matrix)
for i in range(p_matrix.shape[0]):
for j in range(p_matrix.shape[1]):
if p_matrix[i,j] != 0:
mut_info += p_matrix[i,j]*np.log2(p_matrix[i,j]/(p_matrix[i,:].sum()*p_matrix[:,j].sum()))
self.logger.info("信息系数为:{}".format(mut_info/np.log2(min(p_matrix.shape[0],p_matrix.shape[1]))))
return mut_info/np.log2(min(p_matrix.shape[0],p_matrix.shape[1]))
def divide_bin(self,x_num,y_num):
"""
指定在两个变量方向上需划分的网格数,返回概率矩阵
:param x_num:
:param y_num:
:return: p_matrix
"""
p_matrix = np.zeros([x_num,y_num])
x_bin = np.linspace(self.x.min(),self.x.max()+1,x_num+1)
y_bin = np.linspace(self.y.min(),self.y.max()+1,y_num+1)
for i in range(x_num):
for j in range(y_num):
p_matrix[i,j] = sum([1 if (self.x[value] < x_bin[i + 1] and self.x[value] >= x_bin[i] and self.y[value] < y_bin[j + 1] and
self.y[value] >= y_bin[j]) else 0 for value in range(self.x.shape[0])])/self.x.shape[0]
return p_matrix
def cal_MIC(self,x,y):
self.x = np.array(x).reshape((-1,))
self.y = np.array(y).reshape((-1,))
if not self.x_max_num:
self.x_max_num = int(round(self.x.shape[0]**0.3,0))
self.y_max_num = self.x_max_num
self.x_min_num = 2
self.y_min_num = 2
mics = []
for i in range(self.x_min_num,self.x_max_num+1):
for j in range(self.y_min_num,self.x_max_num+1):
self.logger.info("划分区间数量为:[{},{}]".format(i,j))
mics.append(self.cal_mut_info(self.divide_bin(i,j)))
self.logger.info("最大信息系数为:{}".format(max(mics)))
return max(mics)
计算实例
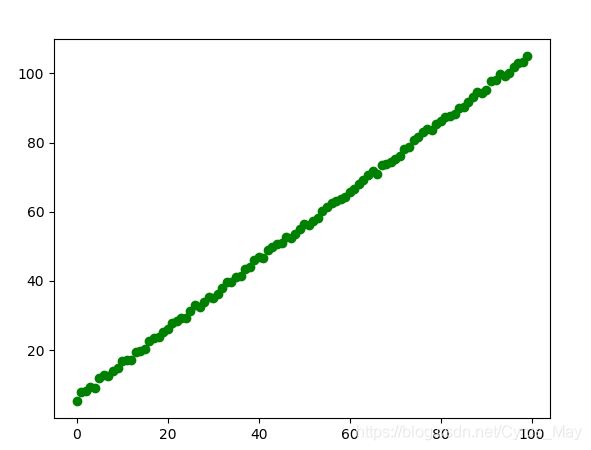
计算加入噪声的线性相关变量的MIC
if __name__ == '__main__':
import matplotlib.pyplot as plt
x = np.arange(0,100)
y = x + 5 + np.array([np.random.random() for i in range(x.shape[0])] )
plt.scatter(x,y,c = 'g')
mic_tool = CyrusMIC()
mic_tool.cal_MIC(x,y)
plt.show()
2020-12-03 17:27:06,617 - MIC.cal_mut_info:41 - INFO - 信息系数为:0.7193485237183258
2020-12-03 17:27:06,618 - MIC.cal_MIC:71 - INFO - 划分区间数量为:[4,2]
2020-12-03 17:27:06,621 - MIC.cal_mut_info:41 - INFO - 信息系数为:1.0
2020-12-03 17:27:06,621 - MIC.cal_MIC:71 - INFO - 划分区间数量为:[4,3]
2020-12-03 17:27:06,631 - MIC.cal_mut_info:41 - INFO - 信息系数为:0.714608689855715
2020-12-03 17:27:06,631 - MIC.cal_MIC:71 - INFO - 划分区间数量为:[4,4]
2020-12-03 17:27:06,643 - MIC.cal_mut_info:41 - INFO - 信息系数为:0.9694248603634986
2020-12-03 17:27:06,643 - MIC.cal_MIC:73 - INFO - 最大信息系数为:1.0
if __name__ == '__main__':
import matplotlib.pyplot as plt
x = np.arange(0,6,0.002)
y = np.sin(x)+5
plt.scatter(x,y,c = 'g')
mic_tool = CyrusMIC()
mic_tool.cal_MIC(x,y)
plt.show()
2020-12-03 17:32:17,002 - MIC.cal_MIC:71 - INFO - 划分区间数量为:[11,9]
2020-12-03 17:32:17,221 - MIC.cal_mut_info:41 - INFO - 信息系数为:0.5534001973540179
2020-12-03 17:32:17,221 - MIC.cal_MIC:71 - INFO - 划分区间数量为:[11,10]
2020-12-03 17:32:17,477 - MIC.cal_mut_info:41 - INFO - 信息系数为:0.540981036470426
2020-12-03 17:32:17,477 - MIC.cal_MIC:71 - INFO - 划分区间数量为:[11,11]
2020-12-03 17:32:17,755 - MIC.cal_mut_info:41 - INFO - 信息系数为:0.5571694750793418
2020-12-03 17:32:17,755 - MIC.cal_MIC:73 - INFO - 最大信息系数为:0.9204753790747687
by CyrusMay 2020 12 03
每颗心 的相信
每个人 的际遇
每个故事的自己
反覆地问着自己
这些年 让步的
你是否 会叹息
——————五月天(顽固)——————