常见数据结构与算法汇总(不断更新)
文章目录
-
- 一、数据结构部分
-
- 1、线性表
-
- 1.1 数组
- 1.2 链表
- 2、栈和队列
- 3、树
-
- 1)二叉树
- 2)二叉搜索树
- 3)平衡二叉树(AVL)
- 4)红黑树
- 4、图
- 5、并查集
- 二、常见算法
-
- 1、回溯
- 2、递归
- 3、动态规划
- 4、滑动窗口
- 5、分治法
- 6、贪心算法
- 7、查找算法
-
- 7.1 线性查找
- 7.2 二分查找
- 7.3 哈希查找
- 8、排序算法
-
- 8.1 快速排序
- 8.2 归并排序
- 8.3 堆排序
一、数据结构部分
1、线性表
1.1 数组
创建数组
//以int型为例
//创建指定大小的数组
int[] nums = new int[len];
//创建多维数组第一个方括号内的数量不可缺失,因为必须为数组分配指定大小的内存。
int[][] nums1 = new int[len][];
int[][][] nums3 = new int[len][][];
//创建并赋初值
int[] nums = {
1, 2, 3};
int[][] nums1 = {
{
1}, {
2}, {
3}};
操作数组
- 复制数组 (nums1复制nums2)
/*对于一维数组来说可以直接通过clone()或arraycopy()方法来进行复制;
但对于多维数组,由于以上两个方法是浅复制,因此需要降至低维进行复制。*/
//一维数组, 下面三种都可以
for(int i = 0; i < len; ++i){
nums1[i] = nums2[i];
}
nums1 = nums2.clone();
nums1 = System.arraycopy(nums2, 0, nums1, 0, n);
//多维数组,以二维为例
for(int i = 0; i < row; ++i){
nums1[i] = nums2[i].clone();
//System.arraycopy(matrix[i],0,copy[i],0,n);//使用arraycopy实现
}
- 遍历数组
//普通遍历
for(int i = 0; i < len; ++i){
system.out.println(nums[i]);
}
//双指针遍历
for(int i = 0, j = len - 1; i < j; ++i, --j){
if(nums[i] == nums[j]){
/*...*/
}
}
- 改变数组
//交换两个数组元素的位置
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
//数组后移/前移
int temp = nums[len - 1];
for(int i = 0; i < len-1; ++i){
nums[i + 1] = nums[i];
}
nums[0] = temp;
int temp = nums[0];
for(int i = len - 1; i > 0; --i){
nums[i - 1] = nums[i];
}
nums[len - 1] = temp;
1.2 链表
创建链表
class Node{
int val;
Node next;
Node(){
}
Node(int x){
this.val = x;
this.next = null;
}
Node(int val, Node next) {
this.val = val;
this.next = next;
}
}
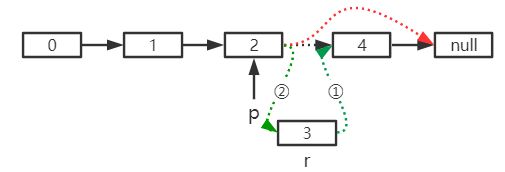
- 删除元素
//对应上图红线
p.next = p.next.next;
- 插入元素
//对应绿线
r.next = p.next;
p.next = r;
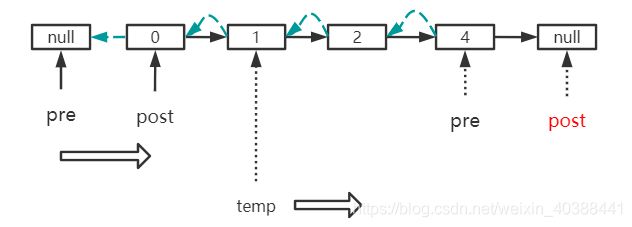
- 修改指针指向(反转链表)
//双指针解法
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode post = head;
while(post != null){
ListNode temp = post.next;
post.next = pre;
pre = post;
post = temp;
}
return pre;
}
//递归法
public ListNode reverseList(ListNode head) {
//递归退出条件:链表为空或到达尾结点,返回
if(head == null || head.next == null){
return head;
}
//cur一直指向尾结点(这里把head作为当前考虑的节点,cur为尾结点好理解一些)
ListNode cur = reverseList(head.next);
//在递归退出的过程中反转指针指向
head.next.next = head;
head.next = null;
return cur;
}
这里采用的第一个解法利用了双指针的思想,双指针思想就是通过两个变量动态存储两个或多个结点,来方便我们进行一些操作,常用于数组和链表中。
常见问题
- 判断有无环
//采用双指针思想,设置两个速度不同的指针遍历链表,如果速度快的跑到了空指针的位置,表明无环,否则一定会相遇。
public boolean hasCycle(ListNode head) {
//快慢指针,快指针追上了慢指针就表明有环
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
if(slow == fast){
return true;
}
}
return false;
}
- 倒数第n个节点的值(进阶:删除倒数第n个节点的值)
//思想比较简单:采用距离指针
public int findLastK(ListNode head, int k){
ListNode p = head;
ListNode q = head;
int i;
for(i = 1; i < k && p.next != null; ++i){
p = p.next;
}
if(i < k) return -1;
while (p.next != null){
p = p.next;
q = q.next;
}
return q.val;
}
- 两条链表的交叉点元素
//暴力遍历:对一条链表的每个节点,都循环遍历另一条链表看是否是相交元素
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
暴力法
while(headA != null){
ListNode nodeB = headB;
while(nodeB != null){
if(headA == nodeB){
return headA;
}
nodeB = nodeB.next;
}
headA = headA.next;
}
return null;
}
//hash映射实现,花空间换时间
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
hash映射实现
Map<ListNode, Integer> map = new HashMap();
while(headA != null){
map.put(headA, 1);
headA = headA.next;
}
while(headB != null){
if(map.containsKey(headB)){
return headB;
}
headB = headB.next;
}
return null;
}
//跑步思想,把两条链形成交叉环,两个指针相遇时一定在交叉点
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//交叉形成环,第二次两个指针一定能到同样的位置(交点或null)
ListNode la = headA;
ListNode lb = headB;
while(la != lb){
//到尾结点交叉
la = (la == null) ? headB : la.next;
lb = (lb == null) ? headA : lb.next;
}
return la;
}
- Leetcode143 重排链表
- Leetcode21 合并两个有序链表
2、栈和队列
栈:先进后出
- 创建:java中可作为栈使用的容器有
Stack和LinkedList,但只要满足栈定义也可用其他数据容器(例如ArrayList)自行实现一个栈。 - 操作:入栈
push(elem)和出栈pop() - 应用:括号匹配,算法的非递归实现(例如树深度搜索算法、回溯算法),单调栈
- 示例:Leetcode1021 删除最外层的括号、Leetcode321 拼接最大数/Leetcode316 去除重复字母(单调栈的运用)
队列:先进先出
- 创建:java中有
Deque,ArrayDeque,LinkedList等,同样可以用其他数据容器自定义实现 - 操作:入队
offer(elem)和出队peek(),根据返回类型的不同还有其他的API共使用 - 应用:层次遍历、任务调度相关算法
特殊:双端队列(两端都可进行入出队操作)、优先级队列等
3、树
1)二叉树
创建二叉树
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(){
}
TreeNode(int x) {
val = x; }
}
操作二叉树
- 前序遍历
递归实现
public void preorderTraversal(TreeNode root){
if(root == null){
return;
}
System.out.println(root.val);
preorderTraversal(root.left);
preorderTraversal(root.right);
}
非递归实现
public void preorderTraversal2(TreeNode root){
if(root == null){
return;
}
Stack<TreeNode> stack = new Stack();
while (root != null || !stack.isEmpty()){
while(root != null){
System.out.println(root.val);
stack.add(root);
root = root.left;
}
TreeNode node = stack.pop();
root = node.right;
}
}
- 中序遍历
递归实现
public void inorderTraversal(TreeNode root){
if(root == null){
return;
}
inorderTraversal(root.left);
System.out.println(root.val);
inorderTraversal(root.right);
}
非递归实现
public void inorderTraversal2(TreeNode root){
if(root == null){
return;
}
Stack<TreeNode> stack = new Stack();
while (root != null || !stack.isEmpty()){
while(root != null){
stack.add(root);
root = root.left;
}
TreeNode node = stack.pop();
System.out.println(node.val);
root = node.right;
}
}
- 后序遍历
递归实现
public void postorderTraversal(TreeNode root){
if(root == null){
return;
}
postorderTraversal(root.left);
postorderTraversal(root.right);
System.out.println(root.val);
}
非递归实现
public void postorderTraversal2(TreeNode root){
if(root == null){
return;
}
Stack<TreeNode> stack = new Stack();
TreeNode lastNode = new TreeNode();
while (root != null || !stack.isEmpty()){
while(root != null){
stack.add(root);
root = root.left;
}
TreeNode node = stack.peek();
if(node.right == null || node.right == lastNode){
stack.pop();
System.out.println(node.val);
lastNode = node;
}else {
root = node.right;
}
}
}
- 层次遍历
public void levelOrder(TreeNode root){
if(root == null){
return;
}
LinkedList<TreeNode> queue = new LinkedList();
queue.add(root);
while (!queue.isEmpty()){
int len = queue.size();
for(int i = 0; i < len; ++i){
TreeNode node = queue.poll();
System.out.println(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
}
}
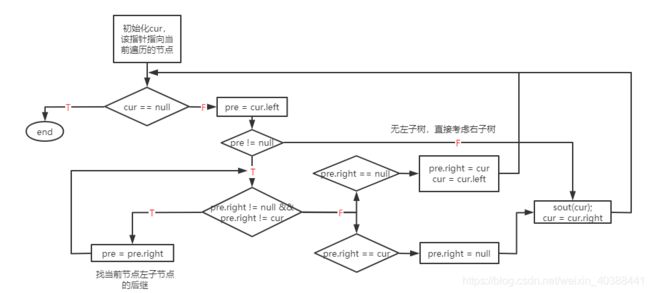
显然,以上遍历方式的空间复杂度为O(n),下面介绍一种空间复杂度为O(1)的遍历算法:Mirrors遍历,其本质是通过线索指针将遍历过程中的前驱和后继关联起来,在构造线索二叉树的过程中进行遍历。
- Mirrors前序遍历
public void morrisPreorder(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode pre = null;
while (cur != null) {
pre = cur.left;
if (pre!= null) {
while (pre.right != null && pre.right != cur) {
pre= pre.right;
}
if (pre.right == null) {
pre.right = cur;
System.out.print(cur.value + " ");
cur = cur.left;
continue;
} else {
pre.right = null;
}
}else{
System.out.print(cur.value + " ");
}
cur = cur.right;
}
}
- Mirrors中序遍历
public void morrisInorder(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode pre = null;
while (cur != null) {
pre = cur.left;
if (pre!= null) {
while (pre.right != null && pre.right != cur) {
pre= pre.right;
}
if (pre.right == null) {
pre.right = cur;
cur = cur.left;
continue;
} else {
pre.right = null;
}
}
System.out.print(cur.value + " ");
cur = cur.right;
}
}
- Mirrors后序遍历
public void morrisPostorder(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode pre = null;
while (cur != null) {
pre = cur.left;
if (pre!= null) {
while (pre.right != null && pre.right != cur) {
pre= pre.right;
}
if (pre.right == null) {
pre.right = cur;
cur = cur.left;
continue;
} else {
pre.right = null;
printNode(cur.left);
}
}
cur = cur.right;
}
printNode(root);
}
//逆序输出当前节点左子树的右边界
private void printNode(TreeNode node) {
LinkedList<Integer> stack = new LinkedList();
while (node!=null){
stack.push(node.val);
node = node.right;
}
while (!stack.isEmpty()){
System.out.println(stack.pop());
}
}
应用:Leetcode501 二叉搜索树中的众数(O(1)空间复杂度的解法)
常见问题
- Leetcode404 左子树之和:深度优先和广度优先
- Leecode112 路径总和、Leetcode113 路径总和 II:深度优先和广度优先
- 根据前序和后序遍历序列构建二叉树
递归法
Map<Integer, Integer> map = new HashMap();
public TreeNode buildTree(int[] preorder, int[] inorder) {
int len = preorder.length;
if(len <= 0) return null;
for(int i = 0; i < len; ++i){
map.put(inorder[i], i);
}
return buildMyTree(preorder, inorder, 0, len-1, 0, len-1);
}
public TreeNode buildMyTree(int[] preorder, int[] inorder, int preL, int preR, int inL, int inR){
if(preL > preR){
return null;
}
int preRoot = preL;
int inRoot = map.get(preorder[preL]);
TreeNode root = new TreeNode(preorder[preRoot]);
int numL = inRoot - inL;
root.left = buildMyTree(preorder, inorder, preL+1, preL+numL, inL, inRoot-1);
root.right = buildMyTree(preorder, inorder, preL+numL+1, preR, inRoot+1, inR);
return root;
}
迭代法
public TreeNode buildTree(int[] preorder, int[] inorder) {
int len = preorder.length;
if(len <= 0) return null;
int index = 0;
LinkedList<TreeNode> stack = new LinkedList();
TreeNode root = new TreeNode(preorder[0]);
stack.push(root);
for(int i = 1; i < len; ++i){
int preorderVal = preorder[i];
TreeNode node = stack.peek();
if(node.val != inorder[index]){
node.left = new TreeNode(preorderVal);
stack.push(node.left);
}else{
while(!stack.isEmpty() && stack.peek().val == inorder[index]){
node = stack.pop();
++index;
}
node.right = new TreeNode(preorderVal);
stack.push(node.right);
}
}
return root;
}
- 二叉树深度
递归
public int maxDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
层次遍历
public int maxDepth(TreeNode root){
if(root == null) return 0;
int height = 0;
Queue<TreeNode> queue = new LinkedList();
queue.add(root);
while(!queue.isEmpty()){
++height;
int n = queue.size();
for(int i = 0; i < n; ++i){
TreeNode node = queue.poll();
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
}
return height;
}
- 二叉树路径(根到叶子)
public List<String> binaryTreePaths(TreeNode root) {
List<String> result = new ArrayList();
constructPaths(root, "", result);
return result;
}
public void constructPaths(TreeNode node, String path, List<String> paths){
if(node != null){
StringBuilder pathSb = new StringBuilder(path);
pathSb.append(Integer.toString(node.val));
if(node.left == null && node.right == null){
paths.add(pathSb.toString());
}else{
pathSb.append("->");
constructPaths(node.left, pathSb.toString(), paths);
constructPaths(node.right, pathSb.toString(), paths);
}
}
}
- Leetcode226 翻转二叉树
public TreeNode invertTree(TreeNode root) {
if(root == null){
return null;
}
//交换左右子节点
TreeNode tmp = root.left;
root.left = invertTree(root.right);
root.right = invertTree(tmp);
return root;
}
实际上,二叉树的应用通常都是几种二叉树操作方式的变体,要点有两个:对二叉树进行何种遍历;在遍历的过程中要收集那些信息。
2)二叉搜索树
性质:
- 每个节点中的值必须大于(或等于)存储在其左侧子树中的任何值;
- 每个节点中的值必须小于(或等于)存储在其右子树中的任何值;
- 所有左子树和右子树自身必须也是二叉搜索树;
操作二叉搜索树
- 查找一个节点
递归方式
public TreeNode findNode(TreeNode root, int val){
if(root == null)
return null;
if(root.val < val) {
return findNode(root.right, val);
}else if(root.val > val){
return findNode(root.left, val);
}else {
return root;
}
}
非递归
与普通二叉树遍历类似,增加节点判断条件
- 插入节点(Leetcode701 二叉搜索树中的插入操作)
递归
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root == null){
return new TreeNode(val);
}else if(root.val > val){
root.left = insertIntoBST(root.left, val);
}else if(root.val < val){
root.right = insertIntoBST(root.right, val);
}
return root;
}
非递归
public TreeNode insertIntoBST(TreeNode root, int val) {
TreeNode tarNode = new TreeNode(val);
if(root == null){
return tarNode;
}
TreeNode cur = root;
while(cur != null){
if(cur.val > val){
if(cur.left == null){
cur.left = tarNode;
break;
}else{
cur = cur.left;
}
}else{
if(cur.right == null){
cur.right = tarNode;
break;
}else{
cur = cur.right;
}
}
}
return root;
}
- 删除节点
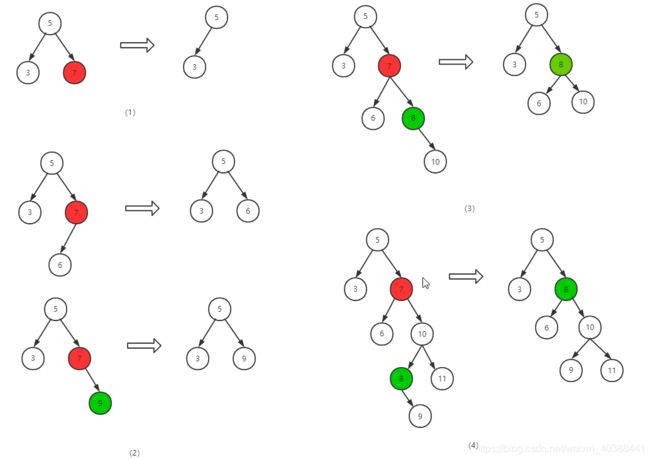
二叉搜索树的删除比较复杂,这里有几种情况需要考虑:
- 删除叶子节点(1)
- 删除非叶子结点
- 单子树
- 直接将子树的根替换目标删除位置(2)
- 双子树
- 后继节点替换目标删除位置
- 所删除元素的后继节点是直接子节点(替换后将待删除节点的左子树加入到后继节点的左子树中的最小位置,右子树不变)(3)
- 所删除元素的后继节点不是直接子节点(替换后将后继节点的左右子树整合后填入原后继节点的位置)(4)
代码
public TreeNode deleteNode(TreeNode root, int val){
if(root == null){
return null;
}
if(root.val < val){
root.right = deleteNode(root.right, val);
return root;
}else if(root.val > val){
root.left = deleteNode(root.left, val);
return root;
}else {
/*分情况讨论*/
TreeNode tmpNode = root;
/*包含情况(1)(2)*/
if(root.right == null){
root = root.left;
return root;
}else if(root.left == null){
root = root.right;
return root;
}
/*包含情况(3)(4)*/
//查找后继节点并替换
tmpNode = findMin(root.right);
//删除右子树的后继节点
tmpNode.right = deleteMin(root.right);
//左子树保持不变
tmpNode.left = root.left;
return tmpNode;
}
}
//查找最小元素
public TreeNode findMin(TreeNode root){
if(root == null){
return null;
}
if(root.left == null) {
return root;
}else {
return findMin(root.left);
}
}
//删除最小元素
public TreeNode deleteMin(TreeNode root){
if(root.left == null){
return root.right;
}else {
root.left = deleteMin(root.left);
return root;
}
}
常见问题
- 创建二叉搜索树
/*nums为一个有序数组,注意二叉搜索树的建立并不唯一*/
public TreeNode sortedArrayToBST(int[] nums) {
return recurse(nums, 0, nums.length-1);
}
public TreeNode recurse(int[] nums, int left, int right){
if(left > right){
return null;
}
int mid = (right + left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = recurse(nums, left, mid-1);
root.right = recurse(nums, mid+1, right);
return root;
}
- 验证是否为二叉搜索树
递归法
public boolean isValidBST(TreeNode root) {
return recurse(root, -Double.MAX_VALUE, Double.MAX_VALUE);
}
public boolean recurse(TreeNode root,double lower,double upper){
if(root == null){
return true;
}
//判断当前节点是否越界
double val = root.val;
if(val <= lower || val >= upper) return false;
//递归判断左右子树
if(!recurse(root.left, lower, val)) return false;
if(!recurse(root.right, val, upper)) return false;
return true;
}
迭代法
public boolean isValidBST(TreeNode root) {
//二叉搜索树中序遍历为一个递增序列
if(root == null){
return true;
}
double lastVal = -Double.MAX_VALUE;
Deque<TreeNode> stack = new LinkedList();
while(!stack.isEmpty() || root != null){
while(root != null){
stack.push(root);
root = root.left;
}
root = stack.pop();
if(root.val <= lastVal){
return false;
}
lastVal = root.val;
root = root.right;
}
return true;
}
- 查找某个值(树上的第k小数)
递归法
List<Integer> res = new ArrayList();
public int kthSmallest(TreeNode root, int k) {
//利用中序遍历二叉搜索树的序列是递增序列这一性质
if(root == null) return 0;
inoder(root);
return res.get(k-1);
}
public void inoder(TreeNode root){
if(root != null){
inoder(root.left);
res.add(root.val);
inoder(root.right);
}
}
迭代法
//遍历到第k个就结束
public int kthSmallest(TreeNode root, int k) {
LinkedList<TreeNode> stack = new LinkedList();
while(true){
while(root != null){
stack.push(root);
root = root.left;
}
root = stack.remove();
if(--k == 0) return root.val;
root = root.right;
}
}
- Leetcode501 二叉搜索树中的众数(结合数组中众数的寻找)
3)平衡二叉树(AVL)
性质:
- 左子树和右子树的深度之差的绝对值不超过1;
- 左子树和右子树都是平衡二叉树;
特别要注意的是,平衡二叉树是基于二叉搜索树的,即平衡二叉树一定是一个二叉搜索树。实际上,二叉平衡树的提出就是为了改进二叉排序树,因为排序树越短,越有利与查找,因此提出了二叉平衡树的概念。
操作二叉平衡树
(与二叉排序树不同,二叉平衡树在插入删除时需要通过旋转操作保持平衡)
- 插入
- 删除
常见问题
(待补充…)
4)红黑树
性质:红黑树是一种含有红黑结点并能自平衡(不是绝对平衡)的二叉查找树。它必须满足下面几个性质:
- 每个节点要么是黑色,要么是红色。
- 根节点是黑色。
- 每个叶子节点(NIL)是黑色。
- 每个红色结点的两个子结点一定都是黑色。
- 任意一结点到每个叶子结点的路径都包含数量相同的黑结点
红黑树相比avl树,在检索的时候效率其实差不多,都是通过平衡来二分查找。但对于插入删除等操作效率提高很多。红黑树不像avl树一样追求绝对的平衡,他允许局部很少的不完全平衡,这样对于效率影响不大,但省去了很多没有必要的调平衡操作,avl树调平衡有时候代价较大,所以效率不如红黑树。
(红黑树的查找、插入和删除操作的时间复杂度都是O(logn))
操作红黑树
(由于树的着色要求,因此红黑树插入删除操作时需要有recolor和rotation的操作)
- 插入
- 删除
应用:红黑树的最重要的应用就是在jdk1.8中HashMap的链表冲突时的数据存储结构,这部分内容会在其他文章中进行讲解。
4、图
表示形式
- 邻接矩阵
- 邻接表
- 十字链表
遍历算法
- 深度优先遍历
Leetcode684 冗余连接
Leetcode529 扫雷游戏(这里的转向操作是一种数组遍历中常用的手段)
- 广度优先遍历
Leetcode127 单词接龙
- A*算法
图的拓扑排序
概念:给定一个包含 n 个节点的有向图 G,我们给出它的节点编号的一种排列,如果满足:对于图 G 中的任意一条有向边 (u, v),u 在排列中都出现在 v 的前面。那么称该排列是图 G 的「拓扑排序」。
- Leetcode详解
最短路径算法
- Dijkstra算法
- Bellman—Ford算法
- Floyd算法
最小生成树
- Prim算法
- Kruskal算法
图匹配算法
- 匈牙利算法
网络流算法
- Ford-Fulkerson算法
- Edmond-Karp算法
- Dinic算法
图的强连通分量求解算法
- Kosaraju
- Gabow
- Tarjan
这些内容慢慢更~
示例
- Leetcode 399 除法求值
问题:给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回所有问题的答案。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。(注:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果)
思路:容易看出这实际上是一个搜索问题,可以把除数与被除数看成是图上的连接关系,那么如果一个查询有解,那么此查询的除数与被除数一定在一个子图中,而搜索结果则对应路径上边的权值计算,该权值由给定的除法结果values确定。由此该问题转变为图上的路径搜索问题,因此存在多种解决方案:
- 深度、广度优先搜索
- Floyd算法
- 带权并查集
//Pair存储被除数index和除数值value,表示图上节点(point)的邻接边
class Pair{
int index;
double value;
Pair(int index, double value){
this.index = index;
this.value = value;
}
}
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
//为方便处理,将字符串映射到整数,代表图中的节点
Map<String,Integer> vars = new HashMap<String,Integer>();
int nvar = 0;
//初始化映射表
int n = equations.size();
for(int i = 0; i < n; ++i){
if(!vars.containsKey(equations.get(i).get(0)))
vars.put(equations.get(i).get(0), nvar++);
if(!vars.containsKey(equations.get(i).get(1)))
vars.put(equations.get(i).get(1), nvar++);
}
//构建邻接表,每个点都包含一个Pair列表以记录邻接边信息
List<Pair>[] edges = new List[nvar];
for(int i = 0; i < nvar; ++i){
edges[i] = new ArrayList<Pair>();
}
for(int i = 0; i < n; ++i){
int va = vars.get(equations.get(i).get(0));
int vb = vars.get(equations.get(i).get(1));
edges[va].add(new Pair(vb, values[i]));
edges[vb].add(new Pair(va, 1.0 / values[i]));
}
//答案查询,对每个答案进行图遍历,寻找结果
int cnt = queries.size();
double[] res = new double[cnt];
for(int i = 0; i < cnt; ++i){
List<String> query = queries.get(i);
double result = - 1.0;
//如果查询中存在映射表中不存在的节点,一定没有结果,不执行查询
if(vars.containsKey(query.get(0)) && vars.containsKey(query.get(1))){
int ia = vars.get(query.get(0)), ib = vars.get(query.get(1));
//除数与被除数相同,结果为1
if(ia == ib){
result = 1.0;
}else{
//dfs查询结果
Queue<Integer> points = new LinkedList<>();
points.offer(ia);
//ratios数组记录ia点与其他点的相除结果
double[] ratios = new double[nvar];
Arrays.fill(ratios, - 1.0);
ratios[ia] = 1.0;
//得到结果或者图搜索完毕则停止搜索
while(!points.isEmpty() && ratios[ib] < 0){
int x = points.poll();
for(Pair pair: edges[x]){
int y = pair.index;
double val = pair.value;
//如果ratios没有计算过,则进行计算
if(ratios[y] < 0){
ratios[y] = ratios[x] * val;
points.offer(y);
}
}
}
result = ratios[ib];
}
}
res[i] = result;
}
return res;
}
}
Floyd算法
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
//为方便处理,将字符串映射到整数,代表图中的节点
Map<String,Integer> vars = new HashMap<String,Integer>();
int nvar = 0;
//初始化映射表
int n = equations.size();
for(int i = 0; i < n; ++i){
if(!vars.containsKey(equations.get(i).get(0)))
vars.put(equations.get(i).get(0), nvar++);
if(!vars.containsKey(equations.get(i).get(1)))
vars.put(equations.get(i).get(1), nvar++);
}
//构建邻接矩阵
double[][] graph = new double[nvar][nvar];
for(int i = 0; i < nvar; ++i){
Arrays.fill(graph[i], -1.0);
}
for(int i = 0; i < n; ++i){
int va = vars.get(equations.get(i).get(0));
int vb = vars.get(equations.get(i).get(1));
graph[va][vb] = values[i];
graph[vb][va] = 1.0 / values[i];
}
//预处理邻接矩阵,将连接关系补全
for(int k = 0; k < nvar; ++k){
for(int i = 0; i < nvar; ++i){
for(int j = 0; j < nvar; ++j){
if(graph[i][k] > 0 && graph[k][j] > 0){
graph[i][j] = graph[i][k] * graph[k][j];
}
}
}
}
//答案查询,直接在邻接矩阵中查询每个答案
int cnt = queries.size();
double[] res = new double[cnt];
for(int i = 0; i < cnt; ++i){
List<String> query = queries.get(i);
double result = - 1.0;
//在邻接矩阵中查询结果信息(除数与被除数相连接则查询成功)
if(vars.containsKey(query.get(0)) && vars.containsKey(query.get(1))){
int ia = vars.get(query.get(0)), ib = vars.get(query.get(1));
if(graph[ia][ib] > 0) result = graph[ia][ib];
}
res[i] = result;
}
return res;
}
带权并查集(介绍在下一小节)
/*带权并查集实现*/
private class UnionFind{
private int[] parent;
private double[] weight;
public UnionFind(int n){
this.parent = new int[n];
this.weight = new double[n];
for(int i = 0; i < n; ++i){
parent[i] = i;
weight[i] = 1.0;
}
}
public void union(int x, int y, double value){
int rootx = find(x);
int rooty = find(y);
//是同一集合则直接返回
if(rootx == rooty) return;
//集合连接
parent[rootx] = rooty;
weight[rootx] = weight[y] * value / weight[x];
}
public int find(int x){
//路径压缩,重新计算权值
if(parent[x] != x){
int origin = parent[x];
parent[x] = find(parent[x]);
weight[x] *= weight[origin];
}
return parent[x];
}
public double isConnected(int x, int y){
int rootx = find(x);
int rooty = find(y);
//是同一集合则返回相除结果res=(x/t)*(t/y)=w[x]/w[y]
if(rootx == rooty){
return weight[x] / weight[y];
}else{
return -1.0;
}
}
}
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
int n = equations.size();
//为方便处理,将字符串映射到整数,代表图中的节点
Map<String,Integer> vars = new HashMap<String,Integer>();
UnionFind unionFind = new UnionFind(2 * n);
//初始化映射表,并将所有节点进行union
int nvar = 0;
for(int i = 0; i < n; ++i){
List<String> equation = equations.get(i);
String var1 = equation.get(0);
String var2 = equation.get(1);
if(!vars.containsKey(var1)) vars.put(var1, nvar++);
if(!vars.containsKey(var2)) vars.put(var2, nvar++);
unionFind.union(vars.get(var1), vars.get(var2), values[i]);
}
//答案查询,在并查集中判查询两个数是否在同一个集合中
int cnt = queries.size();
double[] res = new double[cnt];
for(int i = 0; i < cnt; ++i){
List<String> query = queries.get(i);
Integer id1 = vars.get(query.get(0));
Integer id2 = vars.get(query.get(1));
//不在同一集合中结果为-1.0,否则返回结果
if(id1 == null || id2 == null){
res[i] = -1.0;
}else{
res[i] = unionFind.isConnected(id1, id2);
}
}
return res;
}
5、并查集
概念:并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。可以用于查找树的根节点,判断集合中是否存在某元素,合并集合等。
创建并查集
/*并查集类模板,节点用自然数标识,大小为n*/
class UnionFind {
int[] ancestor;//标识祖先的数组
public UnionFind(int n) {
//初始化并查集
ancestor = new int[n];
for (int i = 0; i < n; ++i) {
ancestor[i] = i;
}
}
public void union(int index1, int index2) {
//合并两个并查集
ancestor[find(index1)] = find(index2);
}
public int find(int index) {
//查找一个元素的根元素
if (ancestor[index] != index) {
//路径压缩
ancestor[index] = find(ancestor[index]);
}
return ancestor[index];
}
}
问题示例
- Leetcode684 冗余连接
class Solution {
int[] result = new int[2];
public int[] findRedundantConnection(int[][] edges) {
int[] parents = new int[edges.length+1];
for(int i = 1; i <= edges.length; ++i){
parents[i] = i;
}
for(int[] edge: edges){
union(edge[0], edge[1], parents);
}
return result;
}
public int find(int x, int[] parents) {
if (x != parents[x]) {
parents[x] = find(parents[x], parents);
}
return parents[x];
}
public void union(int x, int y, int[] parents) {
int rootX = find(x, parents);
int rootY = find(y, parents);
if(rootX != rootY){
parents[rootX] = rootY;
}else{
result[0] = x;
result[1] = y;
}
}
}
- Leetcode685 冗余连接 II
- Leetcode1202 交换字符串中的元素
二、常见算法
1、回溯
算法思想
回溯法一般用于遍历列表的所有子集,一般适用于需要对所有状态都进行遍历才能得到结果的问题。实际上,回溯是DFS的一种,由于需要对所有可能进行穷举,因此复杂度较高,一般为O(n!)。
算法模板
//Type为类型名
Type res = new Type();
public void backtrack(参数列表args){
if(结束条件){
(选择条件)//可选
res.add(目标元素);
return;
}
for(选择列表){
//可选
做选择;
backtrace(参数列表);
撤销选择;
}
}
问题示例
- 全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
/*解法一:交换方式*/
public List<List<Integer>> permute(int[] nums) {
//交换方式的回溯
List<List<Integer>> result = new ArrayList();
List<Integer> list = new ArrayList();
for(int num: nums){
list.add(num);
}
backTrace(result, list, 0, nums.length);
return result;
}
//应用模板
public void backTrace(List<List<Integer>> result, List<Integer> list, int first, int n){
if(first == n){
result.add(new ArrayList<Integer>(list));
return;
}
for(int i = first; i < n; ++i){
Collections.swap(list, first, i);
backTrace(result, list, first+1, n);
Collections.swap(list, first, i);
}
}
/*解法二:增加元素的方式*/
public List<List<Integer>> permute(int[] nums) {
//增加方式的回溯
int len = nums.length;
List<List<Integer>> result = new ArrayList();
List<Integer> list = new ArrayList();
boolean[] flag = new boolean[len];
backTrace(result, list, nums, flag);
return result;
}
//应用模板
public void backTrace(List<List<Integer>> result, List<Integer> list, int[] nums, boolean[] flag){
if(list.size() == nums.length){
result.add(new ArrayList<Integer>(list));
return;
}
for(int i = 0; i < nums.length; ++i){
if(!flag[i]){
list.add(nums[i]);
flag[i] = true;
backTrace(result, list, nums, flag);
flag[i] = false;
list.remove(list.size()-1);
}
}
}
- Leetcode47 全排列II(增加重复元素)
该题的关键在于如何剪枝
- 组合
给两个整数返回1..n中的所有可能的k个组合
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> res = new ArrayList();
if(n < k) return res;
List<Integer> temp = new ArrayList();
backtrack(1, n, k, res, temp);
return res;
//应用模板
public void backtrack(int from, int to, int k, List<List<Integer>> res, List<Integer> temp){
if(temp.size() + to - from + 1 < k) return;
if(temp.size() == k){
//选择条件
res.add(new ArrayList(temp));
return;
}
temp.add(from);//选择头元素
backtrack(from+1, to, k, res, temp);
temp.remove(temp.size()-1);//撤销选择
backtrack(from+1, to, k, res, temp);//不做选择
}
- 组合总和系列(1,2,3)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
说明:
- candidates 中的数字可以无限制重复被选取。
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
List<List<Integer>> res = new ArrayList();
List<Integer> temp = new ArrayList();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);//剪枝所需
backtrack(candidates, 0, target);
return res;
}
public void backtrack(int[] candidates, int index, int count){
if(count == 0){
res.add(new ArrayList(temp));
}else if(count > 0){
//for(int i = index; i < candidates.length; ++i){//不剪枝
for(int i = index; i < candidates.length && count - candidates[i] >= 0; ++i){
//这是剪枝的情况
temp.add(candidates[i]);
backtrack(candidates, i, count - candidates[i]);
temp.remove(temp.size() - 1);
}
}
}
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
说明:
- candidates 中的每个数字在每个组合中只能使用一次。
- 所有数字(包括target )都是正整数。
- 解集不能包含重复的组合。
List<List<Integer>> res = new ArrayList();
List<Integer> temp = new ArrayList();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
backtrack(candidates, 0, target);
return res;
}
public void backtrack(int[] candidates, int cur, int reside){
if(reside == 0){
res.add(new ArrayList(temp));
}else if(reside > 0){
for(int i = cur; i < candidates.length && reside >= candidates[i]; ++i){
if(cur == i || candidates[i] != candidates[i - 1]){
temp.add(candidates[i]);
backtrack(candidates, i+1, reside - candidates[i]);
temp.remove(temp.size() - 1);
}
}
}
}
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
List<List<Integer>> res = new ArrayList();
public List<List<Integer>> combinationSum3(int k, int n) {
List<Integer> temp = new ArrayList();
recall(n, k, 1, temp);
return res;
}
public void recall(int remainder, int k, int cur, List<Integer> temp){
if(remainder == 0 && temp.size() == k){
res.add(new ArrayList(temp));
}else if(remainder > 0){
for(int i = cur; i <= 9 && remainder >= cur; ++i){
temp.add(i);
recall(remainder - i, k, i+1, temp);
temp.remove(temp.size() - 1);
}
}
}
- Leetcode37 解数独
算法优化
如果在回溯的过程中,存在一些一定不需要的状态,那么可以通过对状态空间进行剪枝操作以优化算法性能。示例可参考上面组合总和问题,体现在了for语句中的约束条件reside >= candidates[i]。
2、递归
算法思想
将大问题转化为小问题,通过递归依次解决各个小问题。递归的三要素如下:
- 理解函数需要完成的功能
- 找到递归结束条件
- 找到递归式,即父问题与子问题之间的联系(例如对于阶乘:f(n)=n*f(n-1))
算法模板
//Type为一个数据类型
public Type fun(参数列表){
if(递归结束条件){
return (返回参数);
}
(功能相关的逻辑代码)
return fun(参数列表');//返回fun函数的运算表达式(递归式)或处理结果
}
问题示例
- 斐波那契数列
public static int fibonacci(int n){
if(n <= 2){
//递归结束条件
return 1;
}
return fibonacci(n-1) + fibonacci(n-2);//递归式
}
- 青蛙跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
public static int numWays(int n){
if(n == 0) return 1;
if(n <= 2){
return n;
}
return numWays(n-1) + numWays(n-2);
}
- 反转链表
反转一个单链表
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null){
//递归结束条件
return head;
}
ListNode cur = reverseList(head.next);//递归式
//实现功能所需的逻辑操作
head.next.next = head;//操作1
head.next = null;//操作2
return cur;
}
Tips:在遇到比较难以直观理解的递归思路时,可以尝试把代码中的递归式看成是一个已经定义好的功能函数,然后再观察需要哪些其他的逻辑代码。
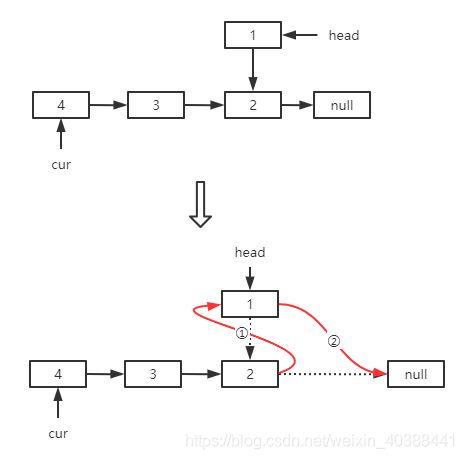
例如对上面的反转链表,假设链表为1->2->3->4,且递归函数的功能和结束条件已经找到:
显然递归结束条件不成立,因此执行递归式,由递归功能可知该递归式输入为结点2,并且处理后连链表形式如下(上半部):
可以看出,结点1并没有达到我们的要求。那次,为了得到我们想要的结果,需要将链表进行修改,如图所示,操作①和②分别对应代码中递归式后的两步操作,最后将处理后的头结点返回即为我们最后的答案。
- Leetcode24 两两交换链表中的节点(与反转链表类似)
- Leetcode386 字典序排数
- Leetcode968 监控二叉树
递推:递归+备忘录
类似回溯,递归在计算子问题时,可能会因为重复计算子问题而导致算法性能下降,因此可以通过空间换时间的方式,增加一个容器存储已经计算的子问题,可以有效的提高算法性能。在后面介绍动态规划时可以看到两者的思想有些类似,实际上,两者解决的问题类型是相同的,但解决方式有些细微的差别,这将在下一节进行说明。
(通过递归+备忘录可以实现动态规划)
3、动态规划
算法思想:动态规划是一种把大问题变成小问题,并解决了小问题重复计算的方法。该算法需要满足最优子结构性质(最优解依赖于子问题解的最优性),四个要素如下:
- 状态(每个问题的结果是什么)
- 方程(状态之间如何进行转移)
- 初始化(初始状态是什么)
- 答案(终止状态是什么)
算法模板
public void dpTemplate(参数列表){
int[] dp = new int[表长n];//或二维int[][] dp
//初始化状态
dp[0] = 0;//或dp[n] = ...
/*代码段*/
for(int i = 1; i <= n; ++i){
//循环处理
/*代码段*/
dp[i] = ... ;//状态转移方程
/*代码段*/
}
/*代码段*/
return dp[n-1];//返回答案
}
上面仅提供了一个大致的框架,使用时要根据实际问题考虑。
使用场景
- 求最大最小值
- 求问题是否可行
- 求可行解的个数
- 解决问题不能进行排序或交换
问题示例
- 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?(实际上跟上面青蛙跳是一个问题)
public int climbStairs(int n) {
if(n<2) return 1;
int[] dp = new int[n];
//初始化
dp[0] = 1;
dp[1] = 2;
for(int i = 2; i < n; ++i){
dp[i] = dp[i-1] + dp[i-2];//状态转移方程
}
return dp[n-1];//返回答案
}
- 序列型问题(最长上升子序列)
给定一个无序的整数数组,找到其中最长上升子序列的长度。
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if(len < 1) return 0;
int[] dp = new int[len];
dp[0] = 1;
int maxres = 1;
for(int i = 1; i < len; ++i){
int max = 0;
for(int j = 0; j < i; ++j){
if(nums[i] > nums[j])
max = Math.max(dp[j], max);
}
dp[i] = max + 1;
maxres = Math.max(maxres, dp[i]);
}
return maxres;
}
- 矩阵型问题(不同路径)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。问总共有多少条不同的路径?
public int uniquePaths(int m, int n) {
int[][] dp = new int[m+1][n+1];
dp[1][1] = 1;
for(int i = 1; i < m+1; ++i){
for(int j = 1; j < n+1; ++j){
if(i != 1 || j != 1)
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m][n];
/*优化空间版
int[] dp = new int[m];
Arrays.fill(dp, 1);
for(int i = 1; i < n; ++i){
for(int j = 1; j < m; ++j){
dp[j] += dp[j-1];
}
}
return dp[m-1];*/
}
一般来说,矩阵型dp问题,可以优化dp空间为一个列表,上面的注释部分代码就是一个示例。
- 背包问题(零钱兑换)
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
自底向上
public int coinChange(int[] coins, int amount) {
if(amount < 1) return 0;
int[] dp = new int[amount+1];
Arrays.fill(dp, amount+1);
dp[0] = 0;
for(int i = 1; i <= amount; ++i){
for(int j = 0; j < coins.length; ++j){
if(coins[j] <= i){
dp[i] = Math.min(dp[i], dp[i - coins[j]]+1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
自顶向下(实际是递推方式的使用)
public int coinChange(int[] coins, int amount) {
if(amount < 1) return 0;
return coinChange(coins, amount, new int[amount]);
}
public int coinChange(int[] coins, int rem, int[] count){
if(rem < 0) return -1;
if(rem == 0) return 0;
if(count[rem-1] != 0) return count[rem-1];
int min = Integer.MAX_VALUE;
for(int coin: coins){
int res = coinChange(coins, rem - coin, count);
if(res != -1) min = Math.min(min, res+1);
}
count[rem-1] = min == Integer.MAX_VALUE ? -1 : min;
return count[rem-1];
}
- Leetcode64 最小路径和
- Leetcode416 分割等和子集
- Leetcode1024 视频拼接
动态规划与递推方法的区别
在上一小节我们提到递推(递归+备忘录)的方法可以解决动态规划问题,经过本小节动态规划的学习之后,其实可以知道动态规划和递推方式的思想是一样的,递推方式只是动态规划的一种形式(自顶向下),但是两者之间还是存在一定的区别:
- 动态规划每个子问题都要解一次,但不会求解重复子问题;递推方法只解哪些确实需要解的子问题;递归方法每个子问题都要解一次,包括重复子问题。
4、滑动窗口
算法思想
双指针思想的一种应用。滑动窗口算法可以用以解决数组/字符串的子元素问题,它可以将嵌套的循环问题,转换为单循环问题,降低时间复杂度。
算法模板
public static void slidingWindow(参数列表){
int left = 0, right = 0;
//Map<> map = new HashMap();用HashMap存储中间结果(可选)
/*代码段...*/
while(窗口移动停止条件){
/*代码段...*/
right++;//右侧窗口移动
/*代码段...*/
while(左侧窗口收缩条件){
//这部分只是对应左侧窗口的更新,形式不固定。
/*代码段...*/
left++;//左侧窗口收缩
/*代码段...*/
}
}
}
问题示例
- 无重复最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
public static int slidingWindow(String str){
int left = 0, right = 0, max = 0, len = 0;
while (right < str.length()){
//窗口滑动停止条件
for(int i = left; i < right; ++i){
//左侧窗口更新操作
if(str.charAt(right) == str.charAt(i)){
left = i+1;//左侧窗口更新
len = right-left;
}
}
right++;//右侧窗口更新
len++;
if(max < len) max = len;
}
return max;
/*hashMap存储版,更符合模板形式*/
/*int left = 0, right = 0, max = 0;
Map map = new HashMap();
while (right < str.length()){
char a = str.charAt(right);
right++;//右滑
map.put(a, map.getOrDefault(a, 0)+1);
for(Character c: map.keySet()){//判断左滑操作
if(map.get(c) > 1){
char b = str.charAt(left);
left++;
map.put(b, map.get(b)-1);
}
}
max = Math.max(max, right - left);
}
return max;*/
}
- 字符串的排列
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。换句话说,第一个字符串的排列之一是第二个字符串的子串。(这里给出的答案一形式与模板差距较大,但还是基于滑动窗口思想,这里只是固定窗口大小滑动)
/*两个窗口都固定,滑动s2的窗口判断是否匹配s1,判断依据窗口内字符的数量情况*/
public boolean checkInclusion(String s1, String s2) {
int len1 = s1.length(), len2 = s2.length();
if(len1 > len2) return false;
int[] s1map = new int[26];
int[] s2map = new int[26];
for(int i = 0; i < len1; ++i){
//两个字符串窗口都为len1大小,计算窗口内字符的对应个数
++s1map[s1.charAt(i) - 'a'];
++s2map[s2.charAt(i) - 'a'];
}
for(int j = len1; j < len2; ++j){
//滑动窗口直至产生结果或到最右端
if(isEqual(s1map, s2map)){
return true;
}
--s2map[s2.charAt(j-len1) - 'a'];
++s2map[s2.charAt(j) - 'a'];
}
return isEqual(s1map, s2map);
}
public boolean isEqual(int[] nums1, int[] nums2){
for(int i = 0; i < 26; ++i){
if(nums1[i] != nums2[i]){
return false;
}
}
return true;
}
模板形式
//s1固定窗口,s2不固定进行滑动,同样在滑动的过程中判断是否匹配
public boolean checkInclusion(String s1, String s2) {
int len1 = s1.length(), len2 = s2.length(), count = 0;
int[] s1map = new int[26];
int[] s2win = new int[26];
for (int i = 0; i < len1; i++) {
//s1的固定大小窗口,记录各个字符的数量情况
if(s1map[s1.charAt(i) - 'a'] == 0)
++count;//不同字符个数
++s1map[s1.charAt(i) - 'a'];
}
int left = 0, right = 0, match = 0;
while (right < len2){
//开始操作窗口
int c = s2.charAt(right) - 'a';
right++;//右侧窗口右滑
if(s1map[c] != 0){
//记录匹配字符个数
++s2win[c];
if(s1map[c] == s2win[c]){
++match;//表示成功匹配字符+1
}
}
while (right - left >= len1){
//判断左侧窗口滑动情况
if(match == count){
//所匹配字符数相同,表明s2滑动窗口成功与s1固定大小的窗口匹配成功
return true;
}
int a = s2.charAt(left) - 'a';
++left;//左侧窗口滑动
if(s1map[a] != 0){
//滑动后修改窗口记录的字符数和匹配数
if(s1map[a] == s2win[a]){
--match;
}
--s2win[a];
}
}
}
return false;
}
5、分治法
算法思想
分治算法的思想就是先分别处理局部问题,再合并结果,常用于解决排序,搜索相关的问题。
算法模板
public Type divide(参数列表){
if(递归退出条件){
//问题规模小到一定程度,返回结果
return (result);//返回结果
}
//分治处理
Type left = divide(参数列表');
Type right = divide(参数列表'');
//合并结果
Type result = Merge from left and right;
return result;
}
问题示例
- 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
public int maxSubArray(int[] nums) {
if(nums.length == 0 || nums == null) return 0;
return branch(nums, 0, nums.length - 1);
}
//分治算法
public int branch(int[] nums, int left, int right){
if(left == right) return nums[left];//递归退出条件
int mid = (left + right) / 2;
int leftSum = branch(nums, left, mid);//子问题1
int rightSum = branch(nums, mid+1, right);//子问题2
int crossSum = crossSum(nums, left, right, mid);//这个不是子问题,只是一段特定的功能代码,封装成了一个函数
return Math.max(Math.max(leftSum, rightSum), crossSum);//根据子问题结果得出父问题结果
}
public int crossSum(int[] nums, int left, int right, int mid){
if(left == right) return nums[left];
int leftSubSum = Integer.MIN_VALUE, curSum = 0;
for(int i = mid; i >= left; --i){
curSum += nums[i];
leftSubSum = Math.max(curSum, leftSubSum);
}
curSum = 0;
int rightSubSum = Integer.MIN_VALUE;
for(int i = mid+1; i <= right; ++i){
curSum += nums[i];
rightSubSum = Math.max(curSum, rightSubSum);
}
return leftSubSum + rightSubSum;
}
(待补充)
6、贪心算法
算法思想
贪心算法是指在问题求解时总是做出当前的最优选择,而不从整体最优上加以考虑,因此实现的是某种意义上的局部最优解(在某些情况下也是全局最优解)。
算法特性
贪心算法有两个重要的特性:
- 贪心选择性
该性质是指问题的整体最优解可以通过一系列局部最优选择来得到。
- 最优子结构
该性质是指一个问题的最优解包含着它子问题的最优解,即问题的整体最优解依赖于其局部子问题解的最优性。
贪心算法与动态规划算法的区别
实际上,从贪心算法的概念可以看出动态规划和贪心算法有一定的相似性,两者的异同如下:
共同点:贪心算法和动态规划算法都要求问题具有最优子结构性质。
不同点:动态规划算法通常以自底向上方式进行(也可以采用自顶向下的递归方式,前面已经讨论过),而贪心算法通常以自顶向下的方式进行,以迭代的方式进行贪心选择,每一次贪心可将问题简化规模更小的子问题。
Tips:对于具有最优子结构性质的问题,如果满足贪心选择性,表明可以通过贪心算法得到问题最优解;否则只能通过动态规划求解问题最优解。例如对于0-1背包问题,贪心算法无法得出最优解,而只能使用动态规划算法。
算法模板
public Type GreedySelector(int n,Type s[],Type f[],bool A[])
{
/*初始化代码*/
for(贪心选择列表){
/*贪心策略*/
}
/*代码段*/
return result;
}
常见应用
- 背包问题
- 活动安排问题
- 哈夫曼编码
- 单源最短路径
- 最小生成树
- 多机调度问题
待补充
问题示例
- 买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
public int maxProfit(int[] prices) {
//即把上升区段的利润值累加
if(prices == null || prices.length == 0)
return 0;
//最大利润
int max = 0;
for(int i = 0; i < prices.length - 1; ++i){
if(prices[i+1] > prices[i]){
//贪心策略:只选择赚钱最多的交易方式
//上升趋势,利润叠加
max += prices[i+1] - prices[i];
}
}
return max;
}
- 跳跃游戏
给定一个非负整数数组,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
public boolean canJump(int[] nums) {
if(nums.length < 2) return true;
int lastPosition = nums.length - 1;
for(int i = lastPosition - 1; i >= 0; --i){
//贪心策略:向前寻找可以到达最左端的位置
if(i+nums[i] >= lastPosition) lastPosition = i;//不断更新可到达的最左端
}
return lastPosition == 0;//最后找到的位置为首位置,表明从首位置可到达尾位置,否则不可以
}
- 跳跃游戏2
给定一个非负整数数组,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。
如何使用最少的跳跃次数到达数组的最后一个位置。
//反向贪心
public int jump(int[] nums) {
if(nums.length < 2) return 0;
int pos = nums.length -1, step = 0;
while(pos != 0){
for(int i = 0; i < pos; ++i){
if(i+nums[i] >= pos){
//贪心策略:从后向前选择最远的一步
pos = i;
++step;
break;
}
}
}
return step;
}
//正向贪心
int len = nums.length;
if(len < 1)
return 0;
int step = 0;
int jump_pos = 0;
int max_pos = 0;
for (int i = 0; i < len - 1; i++) {
//贪心策略:选能跳到最远的位置
max_pos = Math.max(max_pos, nums[i] + i);
if(i == jump_pos){
jump_pos = max_pos;
++step;
if(jump_pos >= len-1)
break;
}
}
return step;
- Leetcode1005 K 次取反后最大化的数组和
- Leetcode1024 视频拼接
7、查找算法
7.1 线性查找
算法思想
该算法是指顺序遍历列表查找目标元素,比较简单,不过多赘述。
算法示例
/*查找指定元素在列表中首次出现的位置,不存在则返回-1*/
public int search(int x, int[] nums){
for(int i = 0; i < nums.length; ++i){
if(nums[i] == x){
return i;
}
}
return -1;
}
7.2 二分查找
算法思想
该算法要求查找结构必须具有随机访问的特点(如数组),是一种用于有序结构中的高效查找算法,其本质是通过中间元素的特点来缩减问题的规模,时间复杂度一般为O(logn)。
算法模板
public int binarySearch(int[] nums, int target) {
int left = 0, right = ...;//初始化查找界限
while(循环退出条件) {
int mid = left + (right - left) / 2;//定义中间元素
//与查找值进行比较
if (nums[mid] == target) {
/*代码段*/
} else if (nums[mid] < target) {
left = ...//更新左边界
} else if (nums[mid] > target) {
right = ...//更新右边界
}
}
return ...;
}
三类查找方式
- 直接查找某元素
public int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
- 列表中存在重复元素,查找最左端目标元素
public int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
//这是为了好理解,实际可以与上面合并成一个条件
// 别返回,收缩左侧边界
right = mid - 1;
}
}
// 最后要检查 left 越界的情况(left到达nums.length)
if (left >= nums.length || nums[left] != target)第二个条件判断是否找到元素
return -1;
return left;
}
简洁版
public int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0;
int right = nums.length;
while (left < right) {
int mid = (left + right) / 2;
if(nums[mid] >= target) {
right = mid;
}else {
left = mid + 1;
}
}
return left;
}
- 列表中存在重复元素,查找最右端目标元素
public int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
}
}
// 最后要检查 right 越界的情况(right到达-1)
if (right < 0 || nums[right] != target)//第二个条件判断是否找到元素
return -1;
return right;
}
简洁版
public int right_bound(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = (left + right) / 2;
if(nums[mid] <= target) {
left = mid + 1;
}else {
right = mid;
}
}
return right - 1;
问题示例
- 第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
采用类别二简洁版
public int firstBadVersion(int n) {
int start = 1;
int end = n;
while(start < end){
int mid =start + (end - start) / 2;
if(isBadVersion(mid)){
end = mid;
}else{
start = mid+1;
}
}
return start;
}
- 搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
- 可以假设数组中不存在重复的元素。
- 算法时间复杂度必须是 O(log n) 级别。
采用类别一
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right){
int mid = (left+right) / 2;
if(nums[mid] == target) return mid;
if((target >= nums[left]) ^ (nums[left] > nums[mid]) ^ (nums[mid] >= target))
left = mid + 1;
else
right = mid - 1;
}
return -1;
}
- 寻找两个正序数组的中位数
给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。假设 nums1 和 nums2 不会同时为空,请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。本题代码参考了博主windliang的解法4。
还是属于类别一,不过针对问题进行了扩充
public double findMedianSortedArrays(int[] A, int[] B) {
int m = A.length;
int n = B.length;
if (m > n) {
return findMedianSortedArrays(B,A); // 保证 m <= n
}
int iMin = 0, iMax = m;
while (iMin <= iMax) {
int i = (iMin + iMax) / 2;
int j = (m + n + 1) / 2 - i;
if (j != 0 && i != m && B[j-1] > A[i]){
// i 需要增大
iMin = i + 1;
}
else if (i != 0 && j != n && A[i-1] > B[j]) {
// i 需要减小
iMax = i - 1;
}
else {
//根据奇偶情况输出元素
int maxLeft = 0;
//移动到边界
if (i == 0) {
maxLeft = B[j-1];
}else if (j == 0) {
maxLeft = A[i-1];
}else {
//找到分界位置,判断左边最大元素
maxLeft = Math.max(A[i-1], B[j-1]);
}
// 奇数的话不需要考虑右半部分,直接输出单个元素
if ( (m + n) % 2 == 1 ) {
return maxLeft;
}
//偶数和找到最小右元素
int minRight = 0;
if (i == m) {
minRight = B[j];
}else if (j == n) {
minRight = A[i];
}else {
minRight = Math.min(B[j], A[i]);
}
return (maxLeft + minRight) / 2.0; //如果是偶数的话返回结果
}
}
return 0.0;
}
- Leetcode 53 在排序数组中查找数字
本节参考了一位博主关于二分查找的文章,讲得非常好。
7.3 哈希查找
算法思想
哈希表是一种根据键(Key)直接访问在内存存储位置的数据结构。它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度。这个映射函数称做散列函数,存放记录的数组称做散列表(哈希表)。哈希查找就是一种用哈希表存储结果,并根据键进行查找的方式。
这部分内容比较简单,在使用时一般是将结果存储在哈希表中,再通过散列函数进行查找
算法示例
- 存在重复元素
给定一个整数数组,判断是否存在重复元素。如果任意一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。
public boolean containsDuplicate(int[] nums) {
int len = nums.length;
//用hash表进行数字出现的记录,实际上是利用了hash查找
HashMap hashMap = new HashMap();
for(int i = 0; i < len; ++i){
if(hashMap.containsKey(nums[i])){
//hash查找
return true;
}else{
//查找不到则将新元素添加进hash表
hashMap.put(nums[i], 1);
}
}
return false;;
}
- 两个数组的交集 II
给定两个数组,编写一个函数来计算它们的交集。
public int[] intersect(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
if(len1 > len2) intersect(nums2, nums1);
Map<Integer, Integer> map= new HashMap();
int[] result = new int[len1];
int index = 0;
for(int i = 0; i < len1; ++i){
if(map.containsKey(nums1[i])){
map.put(nums1[i], map.get(nums1[i])+1);
}else{
map.put(nums1[i], 1);
}
}
for(int j = 0; j < len2; ++j){
if(map.containsKey(nums2[j])){
int count = map.get(nums2[j]);
if(count > 0){
result[index++] = nums2[j];
map.put(nums2[j], --count);
if(count <= 0){
map.remove(nums2[j]);
}
}
}
}
return Arrays.copyOfRange(result, 0, index);
}
8、排序算法
这部分形式比较固定,直接上模板。
8.1 快速排序
public class QuickSortTest {
public int[] quickSort(int[] nums){
quickSort(nums, 0, nums.length - 1);
return nums;
}
public void quickSort(int[] nums, int start, int end){
if (start < end){
int mid = partition(nums, start, end);
//根据当前基准位置分治处理
quickSort(nums, 0, mid - 1);
quickSort(nums, mid + 1, end);
}
}
//计算基准值的排序位置
public int partition(int[] nums, int start, int end){
int base = nums[end];
int cur = start;
//将比基准值小的元素一律往前放
for(int j = start; j < end; j++){
if(nums[j] < base){
swap(nums, cur, j);
++cur;
}
}
swap(nums, cur, end);
return cur;
}
public void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
//测试代码
public static void main(String[] args) {
int[] nums = {
9,6,4,7,2,3};
QuickSortTest quickSortTest = new QuickSortTest();
quickSortTest.quickSort(nums);
for (int n: nums) {
System.out.println(n);
};
}
}
8.2 归并排序
public class MergeSortTest {
public int[] mainSort(int[] nums){
mergeSort(nums, 0, nums.length - 1, new int[nums.length]);
return nums;
}
public void mergeSort(int[] nums, int left, int right, int[] temp){
if(right > left){
int mid = (left + right) / 2;
mergeSort(nums, left, mid, temp);
mergeSort(nums, mid+1, right, temp);
merge(nums, left, mid, right, temp);
}
}
public void merge(int[] nums, int left, int mid, int right, int[] temp){
int l = left;//左边序列起始位置
int r = mid + 1;//右边序列起始位置
int index = 0;//临时数组填充位置
while(l <= mid && r <= right){
if(nums[l] > nums[r]){
temp[index++] = nums[r];
++r;
}else {
temp[index++] = nums[l];
++l;
}
}
//将多余部分填入临时数组
while(l <= mid){
temp[index++] = nums[l++];
}
while(r <= right){
temp[index++] = nums[r++];
}
//将临时数组的值赋给结果数组
for(int j = 0; j < index; ++j){
nums[left + j] = temp[j];
}
}
//测试代码
public static void main(String[] args) {
int[] nums = {
7, 5, 4, 2, 9, 6, 15};
MergeSortTest mergeSortTest = new MergeSortTest();
mergeSortTest.mainSort(nums);
for (int n: nums) {
System.out.println(n);
}
}
}
8.3 堆排序
public class HeapSortTest {
public void heapSort(int[] nums){
//创建堆,将原始数组构建成一个大顶堆
int len = nums.length;
for(int i = (len - 1) / 2; i >= 0; --i){
adjustHeap(nums, len, i);
}
//将堆顶元素与末尾元素交换
for(int i = len - 1; i > 0; --i){
swap(nums, 0, i);
//交换完后调整树结构(针对堆顶)
adjustHeap(nums, i, 0);
}
}
//递归调整堆结构
public void adjustHeap(int[] nums, int len, int cur){
if(cur >= len){
return;
}
int lChild = 2 * cur + 1;
int rChild = 2 * cur + 2;
int max = cur;
//判断子结点是否比父节点大
if(lChild < len && nums[lChild] > nums[max]){
max = lChild;
}
if(rChild < len && nums[rChild] > nums[max]){
max = rChild;
}
//如果父节点不是最大的,交换元素并递归调整
if(max != cur){
swap(nums, max, cur);
adjustHeap(nums, len, max);
}
}
public void swap(int[] nums, int i, int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
//测试代码
public static void main(String[] args) {
int[] nums = {
15, 8, 1, 19, 16, 9};
HeapSortTest heapSortTest = new HeapSortTest();
heapSortTest.heapSort(nums);
for (int n: nums) {
System.out.println(n);
}
}
}
上面的排序算法所采用的的数据结构是数组形式,对于链表形式的相关排序算法如下:
冒泡排序
public ListNode sortList(ListNode head) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode preHead = dummy;
while(head != null){
ListNode cur = head.next, preCur = head;
while(cur != null){
if(cur.val < head.val){
preCur.next = cur.next;
cur.next = head;
preHead.next = cur;
head = cur;
cur = preCur.next;
}else{
cur = cur.next;
preCur = preCur.next;
}
}
preHead = head;
head = head.next;
}
return dummy.next;
插入排序
public ListNode sortList(ListNode head) {
ListNode dummy = new ListNode(0);
ListNode pre = dummy;
while(head != null){
ListNode tmp = head.next;
if(pre.val > head.val) pre = dummy;
while(pre.next != null && pre.next.val < head.val){
pre = pre.next;
}
head.next = pre.next;
pre.next = head;
head = tmp;
}
return dummy.next;
归并排序(自顶向下)
public ListNode sortList(ListNode head) {
return sortList(head, null);
}
//快慢指针寻找中间节点
public ListNode sortList(ListNode head, ListNode tail){
if(head == tail){
return head;
}
if(head.next == tail){
head.next = null;
return head;
}
ListNode slow = head, fast = slow;
while(fast != tail && fast.next != tail){
slow = slow.next;
fast = fast.next.next;
}
ListNode mid = slow;
ListNode list1 = sortList(head, mid);
ListNode lsit2 = sortList(mid, tail);
return mergeSort(list1, lsit2);
}
//合并两个有序链表
public ListNode mergeSort(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0);
dummy.next = l1;
ListNode curNode = dummy;
while(l1 != null && l2 != null){
if(l1.val >= l2.val){
curNode.next = l2;
l2 = curNode.next.next;
curNode.next.next = l1;
}else{
l1 = l1.next;
}
curNode = curNode.next;
}
curNode.next = l1 != null ? l1 : l2;
return dummy.next;
归并排序(自底向上)
public ListNode sortList(ListNode head) {
if(head == null){
return head;
}
// 1. 首先从头向后遍历,统计链表长度
int length = 0; // 用于统计链表长度
ListNode node = head;
while(node != null){
length++;
node = node.next;
}
// 2. 初始化 引入dummynode
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
// 3. 每次将链表拆分成若干个长度为subLen的子链表 , 并按照每两个子链表一组进行合并
for(int subLen = 1;subLen < length;subLen <<= 1){
// subLen每次左移一位(即sublen = sublen*2) PS:位运算对CPU来说效率更高
ListNode prev = dummyHead;
ListNode curr = dummyHead.next; // curr用于记录拆分链表的位置
while(curr != null){
// 如果链表没有被拆完
// 3.1 拆分subLen长度的链表1
ListNode head_1 = curr; // 第一个链表的头 即 curr初始的位置
for(int i = 1; i < subLen && curr != null && curr.next != null; i++){
// 拆分出长度为subLen的链表1
curr = curr.next;
}
// 3.2 拆分subLen长度的链表2
ListNode head_2 = curr.next; // 第二个链表的头 即 链表1尾部的下一个位置
curr.next = null; // 断开第一个链表和第二个链表的链接
curr = head_2; // 第二个链表头 重新赋值给curr
for(int i = 1;i < subLen && curr != null && curr.next != null;i++){
// 再拆分出长度为subLen的链表2
curr = curr.next;
}
// 3.3 再次断开 第二个链表最后的next的链接
ListNode next = null;
if(curr != null){
next = curr.next; // next用于记录 拆分完两个链表的结束位置
curr.next = null; // 断开连接
}
// 3.4 合并两个subLen长度的有序链表
ListNode merged = mergeTwoLists(head_1,head_2);
prev.next = merged; // prev.next 指向排好序链表的头
while(prev.next != null){
// while循环 将prev移动到 subLen*2 的位置后去
prev = prev.next;
}
curr = next; // next用于记录 拆分完两个链表的结束位置
}
}
// 返回新排好序的链表
return dummyHead.next;
}
// 此处是Leetcode21 --> 合并两个有序链表
public ListNode mergeTwoLists(ListNode l1,ListNode l2){
ListNode dummy = new ListNode(0);
ListNode curr = dummy;
while(l1 != null && l2!= null){
// 退出循环的条件是走完了其中一个链表
// 判断l1 和 l2大小
if (l1.val < l2.val){
// l1 小 , curr指向l1
curr.next = l1;
l1 = l1.next; // l1 向后走一位
}else{
// l2 小 , curr指向l2
curr.next = l2;
l2 = l2.next; // l2向后走一位
}
curr = curr.next; // curr后移一位
}
// 退出while循环之后,比较哪个链表剩下长度更长,直接拼接在排序链表末尾
if(l1 == null) curr.next = l2;
if(l2 == null) curr.next = l1;
// 最后返回合并后有序的链表
return dummy.next;
快速排序(值交换)
public ListNode sortList(ListNode head) {
quickSort(head, null);
return head;
}
public void quickSort(ListNode head, ListNode tail){
if(head == tail || head.next == tail) return;
int pivot = head.val;
ListNode left = head, cur = head.next;
while(cur != tail){
if(cur.val < pivot){
left = left.next;
swap(left, cur);
}
cur = cur.next;
}
swap(head, left);
quickSort(head, left);
quickSort(left.next, tail);
}
public void swap(ListNode n1, ListNode n2){
int tmp = n1.val;
n1.val = n2.val;
n2.val = tmp;
}
快速排序(指针交换)
public ListNode sortList(ListNode head) {
return quickSort(head);
}
ListNode quickSort(ListNode head){
if(head == null || head.next == null) return head;
int pivot = head.val;
// 链表划分
ListNode ls = new ListNode(-1), rs = new ListNode(-1);
ListNode l = ls, r = rs, cur = head;
while(cur != null){
if(cur.val < pivot){
l.next = cur;
l = l.next;
}else{
r.next = cur;
r = r.next;
}
cur = cur.next;
}
l.next = rs.next;
r.next = null;
// 递归调用,先重排右边的,再把指针置空,再重排左边的
ListNode right = quickSort(head.next);
head.next = null;
ListNode left = quickSort(ls.next);
// 拼接左半部分和右半部分
cur = left;
while(cur.next != null){
cur = cur.next;
}
cur.next = right;
return left;
}
其他:基数排序、桶排序:Leetcode164 最大间距
这部分只列举出了常考的排序方式,更详细的内容可以参考博主像素的文章