算法分析课设(九)LED Display
Input:
The input consists of several test cases. The first line of each test case contains a positive integer N (<=1000), then followed by a list of N digits. Each digit follows with a blank space.
题目
One day in the laboratory, Fred found some LED displays. This seven-segment LED can display digit 0 to 9 properly. But Fred soon find the LED have a serious problem, at the beginning, the seven bars were all on. But when one bar once was trun off, it can't be turn on again! So ecah LED only can display digit in certain oder. For example, one LED can display 9,3,7 successively, but can't display 2,4.
Now, Fred have a task to display a sequence of digit that is between 0 to 9. Because of the shortcoming of these LEDs, he need a number of them. But he also want to minimize the number, can you help him?
NOTE:If two digits in a sequece are the same,Fred want for the clearness, so he thought the latter digit can't be displayed on the same LED.
Input:
The input consists of several test cases. The first line of each test case contains a positive integer N (<=1000), then followed by a list of N digits. Each digit follows with a blank space.
Output:
For each test case, you must print a minimum number of LED that Fred need in one line.
Sample Input:
1
8
4
9 0 7 3
8
8 8 8 9 6 5 4 1
Sample Output:
1
2
3
分析
题意是,一个led有7个灯,比如显示数字8的时候,7个灯全亮的。现在这7个灯出故障了,第一次显示了数字,比如9,它有一个灯是不亮的,那么后面显示的数字那个灯也不能亮,比如0,2,6,8是不能显示的,但是1,3,4,5,7可以。现在给定一个数字序列,要求按顺序显示这些数字最少需要几个led。如果输入是8,那么下一次显示的可以是除了8外的所有数。
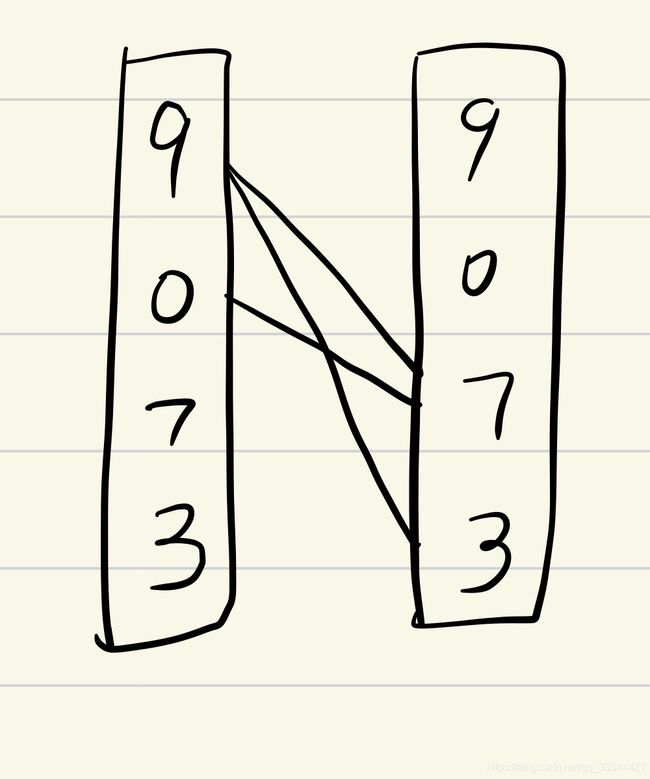
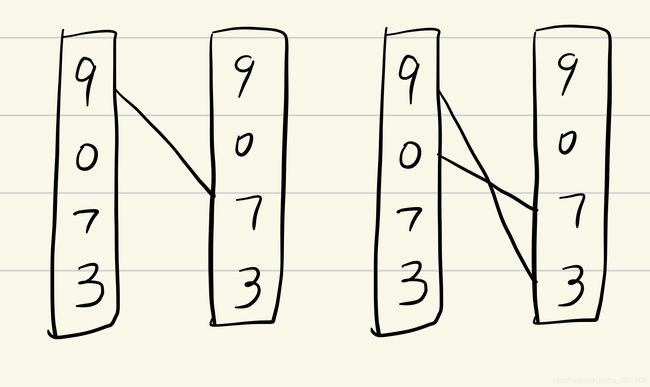
这里要用到二分图。左侧在右侧寻找匹配的点,比如led显示9之后,这个led只能显示7或者3了,这里9连7,3。而0只能连7,所以9不能再连7了。
现在我们输入这串数字序列,就拿 [9,0,7,3] 举例。
int main() {
//输入序列中数字的个数n
while(~scanf("%d", &n)) {
//输入序列中n个数字的值,并存入数组num
for (int i = 1; i <= n; ++i)
scanf("%d", &num[i]);
//构造有向无环图
build();
//执行匈牙利算法寻找最大匹配
//最小边覆盖=总结点数-最大匹配数
printf("%d\n", n - hungary());
}
return 0;
}build需要构造好邻接矩阵,作为判断led的第二次和后面n次能否某个数字。
void build() {
memset(Map, 0, sizeof(Map));//对邻接矩阵map进行初始化
for (int i = 1; i < n; ++i) {
for (int j = i + 1; j <= n; ++j) {
if (num[i] == 0) {//数字可由0变为1或7
if (num[j] == 1) Map[i][j] = 1;
if (num[j] == 7) Map[i][j] = 1;
} else if (num[i] == 3) {//数字可由3变为1或7
if (num[j] == 1) Map[i][j] = 1;
if (num[j] == 7) Map[i][j] = 1;
} else if (num[i] == 4) {//数字可由4变为1
if (num[j] == 1) Map[i][j] = 1;
} else if (num[i] == 6) {//数字可由6变为5
if (num[j] == 5) Map[i][j] = 1;
} else if (num[i] == 7) {//数字可由7变为1
if (num[j] == 1) Map[i][j] = 1;
}
//若数字为8,则全亮,可变为任意数字
//但根据题意,不能连续显示两个相同的数字,故8存在除到自身以外的9条路径
else if (num[i] == 8 &&
num[j] != 8) Map[i][j] = 1;
else if (num[i] == 9) {//数字可由9变为1,3,4,5,7
if (num[j] == 1) Map[i][j] = 1;
if (num[j] == 3) Map[i][j] = 1;
if (num[j] == 4) Map[i][j] = 1;
if (num[j] == 5) Map[i][j] = 1;
if (num[j] == 7) Map[i][j] = 1;
}
}
}
}这一步就是完成map表的填写。后面匹配的时候回来查表。
构造完后,进行匈牙利算法,它能算出最多能匹配的数字。
//匈牙利算法寻找最大匹配
int hungary () {
// 匹配成功数
int res = 0;
// 初始化linker数组。它是用来存放已经匹配了的右侧点对应的左侧点
// 比如9连上了7,但是后面0要连7,就要通过此数组找到9,重新别的线
memset(linker, -1, sizeof(linker));
// 从左侧集中的第一个元素开始,在右侧找能连线的数
for (int u = 0; u < n; ++u) {
// 重置vis数组
memset(vis, 0, sizeof(vis));
// 匹配成功则res加1。反之匹配数不变
if (dfs(u))
++res;
}
return res;
}递归函数dfs,用来连线的。
// 连线进行匹配。它是递归函数
// 匹配不成功有两种情况,1、右侧没有匹配的数,返回false
// 2、匹配的数被连线了。dfs给被占用数对应的左侧的数
// 传入左侧点
bool dfs (int u) {
// 遍历右侧点
for (int v = 0; v < n; ++v) {
// u和v能连,v且没被连过
if (Map[u][v] && !connected[v]) {
// 标记v被连线了
connected[v] = 1;
// 1、如果这个点没有左侧数,比如9连7的时候7没有左侧数
// 2、如果这个点有左侧数,则左侧数重新找右侧数,比如9连了7后,0连7时就会进入dfs,把9重新连到别处
if (linker[v] == -1 || dfs(linker[v])) {
// 让u成为v的前一个显示数
linker[v] = u;
return true;
}
}
}
// 循环结束,仍未找到匹配,返回匹配失败
return false;
}完整代码
#include
#include
#include
using namespace std;
const int MAX = 1005;
int n;
int num[MAX], Map[MAX][MAX];
int linker[MAX], connected[MAX];
//假设num=[9,0,7,3]
//9可到达7,故map[1][3]=1
void build() {
memset(Map, 0, sizeof(Map));//对邻接矩阵map进行初始化
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
if (num[i] == 0) {//数字可由0变为1或7
if (num[j] == 1) Map[i][j] = 1;
if (num[j] == 7) Map[i][j] = 1;
} else if (num[i] == 3) {//数字可由3变为1或7
if (num[j] == 1) Map[i][j] = 1;
if (num[j] == 7) Map[i][j] = 1;
} else if (num[i] == 4) {//数字可由4变为1
if (num[j] == 1) Map[i][j] = 1;
} else if (num[i] == 6) {//数字可由6变为5
if (num[j] == 5) Map[i][j] = 1;
} else if (num[i] == 7) {//数字可由7变为1
if (num[j] == 1) Map[i][j] = 1;
}
//若数字为8,则全亮,可变为任意数字
//但根据题意,不能连续显示两个相同的数字,故8存在除到自身以外的9条路径
else if (num[i] == 8 &&
num[j] != 8) Map[i][j] = 1;
else if (num[i] == 9) {//数字可由9变为1,3,4,5,7
if (num[j] == 1) Map[i][j] = 1;
if (num[j] == 3) Map[i][j] = 1;
if (num[j] == 4) Map[i][j] = 1;
if (num[j] == 5) Map[i][j] = 1;
if (num[j] == 7) Map[i][j] = 1;
}
}
}
}
// 连线进行匹配。它是递归函数
// 匹配不成功有两种情况,1、右侧没有匹配的数,返回false
// 2、匹配的数被连线了。dfs给被占用数对应的左侧的数
// 传入左侧点
bool dfs (int u) {
// 遍历右侧点
for (int v = 0; v < n; ++v) {
// u和v能连,v且没被连过
if (Map[u][v] && !connected[v]) {
// 标记v被连线了
connected[v] = 1;
// 1、如果这个点没有左侧数,比如9连7的时候7没有左侧数
// 2、如果这个点有左侧数,则左侧数重新找右侧数,比如9连了7后,0连7时就会进入dfs,把9重新连到别处
if (linker[v] == -1 || dfs(linker[v])) {
// 让u成为v的前一个显示数
linker[v] = u;
return true;
}
}
}
// 循环结束,仍未找到匹配,返回匹配失败
return false;
}
//匈牙利算法寻找最大匹配
int hungary () {
// 匹配成功数
int res = 0;
// 初始化linker数组。它是用来存放已经匹配了的右侧点对应的左侧点
// 比如9连上了7,但是后面0要连7,就要通过此数组找到9,重新别的线
memset(linker, -1, sizeof(linker));
// 从左侧集中的第一个元素开始,在右侧找能连线的数
for (int u = 0; u < n; ++u) {
// 重置connected数组
memset(connected, 0, sizeof(connected));
// 匹配成功则res加1。反之匹配数不变
if (dfs(u))
++res;
}
return res;
}
int main() {
//输入序列中数字的个数n
while(~scanf("%d", &n)) {
//输入序列中n个数字的值,并存入数组num
for (int i = 0; i < n; ++i)
scanf("%d", &num[i]);
//构造有向无环图
build();
//执行匈牙利算法寻找最大匹配
//最小边覆盖=总结点数-最大匹配数
printf("%d\n", n - hungary());
}
return 0;
}